BIOMASS STOVES:
ENGINEERING DESIGN,
DEVELOPMENT, AND
DISSEMMINATION
By
Samuel F.
Baldwin
Princeton University
Support for the
publication of
this volume was
provided by
the Directorate
General
for Development
Cooperation
Ministry of Foreign
Affairs
Government of the
Netherlands
VITA
1600 Wilson Boulevard,
Suite 500
Arlington, Virgnia
22209 USA
Tel: 703/276-1800 . Fax:
703/243-1865
Internet:
pr-info@vita.org
Center For Energy and
Environmental Studies
Princeton
University
Princeton, New Jersey
08544 USA
Biomass
Stoves
Copyright
[sup.c] 1987 Volunteers in Technical Assistance
All rights
reserved. No part of this publication may be produced or transmitted
in any form
or by any means, electronic or mechanical, including photocopy,
recording, or
any information storage and retrieval system without the written
permission of
the publisher.
Manufactured
in the United States of America.
Published by
VITA
1600 Wilson Boulevard,
Suite 500
Arlington, Virgnia 22209 USA
Library of
Congress Cataloging-in-Publication Data
Baldwin,
Samuel F., 1952-
Biomass stoves.
Bibliography: p.
Includes index.
1. Biomass stoves--Design and construction.
2. Biomass energy--Developing countries. 3.
Fuelwood--
Conservation--Developing countries. I. Title
TH7436.5.B35 1987
683'.88 87-6107
ISBN 0-86619-274-3
To my sister, Hannah
ACKNOWLEDGEMENTS
The work
presented in this volume began in West Africa, under the auspices
of a
long-term project implemented by Volunteers in Technical Assistance
(VITA) and
the Comite Permanent Inter-etats de Lutte Contre la Secheresse
dans le Sahel
(CILSS). Since then, numerous people and organizations have
assisted at
every step in its development. Many of the contributors have
been
carefully noted in the detailed references and so will not be
repeated
here. However, special thanks are due
the following:
For financial
support while in Africa: United States Agency for International
Development
and IBM-Europe.
For
institutional support while in Africa: CILSS, Ouagadougou; l'Institut
Burkinabe de
l'Energie (IBE), Ouagadougou; Mission Forestiere Allemand
(MFA),
Ouagadougou; Laboratoire d'Energie Solaire (LESO), Bamako; Centre
des Etudes et
des Recherches des Energies Renouvelables (CERER), Dakar;
Association
Bois de Feu, Marseille; Association pour le Developpement des
Energies
Renouvelables en Mauritanie (ADEREM), Nouakchott; Church World
Service
(CWS), Niamey; United States Agency for International Development
(USAID); and
United States Peace Corps.
For partial
financial support in the U.S.: World Resources Institute and
the
Rockefeller Brothers Foundation, The Hewlett Foundation, the Center
for Energy
and Environmental Studies of Princeton University, and VITA.
For
illustrations and graphics assistance:
Ellen Thomson, Thomas O.
Agans, and
Mike Freeman.
For editorial
and production assistance: Julie
Berman, Margaret Crouch,
Juleann
Fallgatter, Maria Garth, and Jim Steward of VITA.
For review
comments and suggestions: Alfredo
Behrens, Margaret Crouch,
Gautam Dutt,
Eric Larson, Cliff Hurvich, Eric Hyman, Willett Kempton,
Robert
Morgan, H.S. Mukunda, Tom Norton, Kirk Smith, Bob Williams, and
Timothy Wood.
For providing
optical scanning equipment: Charles Creesy of Princeton
University.
For
preparation and publication support: The Hewlett Foundation, the
Center for
Energy and Environmental Studies, and VITA.
Simply
listing those who have helped, however, does not adequately
describe the
critical role that so many have played in this work.
The
original
improved stoves project with CILSS began in 1980 when IBM-Europe
approached
VITA with a request to design a program with CILSS for the
research and
development of improved stoves as a way to combat deforestation.
USAID later
provided funds to keep this program going. It was the
foresight and
unwavering support of these two organizations -- the aid
agency and
the corporation -- that allowed this work to take place at all.
Timothy Wood
was the first Technical Coordinator of the VITA/CILSS
improved
stove project and it was his fine work in organizing many of the
national
projects and in beginning the development of fired clay stoves
that, in
large part, paved the way for the work described here.
Following my
arrival in West Africa as the second Technical Coordinator,
the work
described was made possible only through assistance far above and
beyond the
call of duty by: Issoufou Ouedraogo, Georges Yameogo, Frederic
Yerbanga, and
Stephen and Cornelia Sepp in Burkina Faso; Yaya Sidibe,
Cheick
Sanogo, and Terry Hart in Mali; Massaer Gueye, Lamine Diop, and
Susan
Farnsworth in Senegal; Ralph Royer in Niger; Bill Phelan in Mauritania;
and above
all, Moulaye Diallo of CILSS and Sylvain Strasfogel of
Association
Bois de Feu. At the same time, I received superb support from
Paula Gubbins
and Juleann Fallgatter at VITA headquarters.
Many, many
others also
helped significantly and to them I must apologize for not
specifically
citing their names here.
With my
return to the United States I have continued to receive invaluable
assistance
from many sources. Among those listed
above, special thanks
are due
Margaret Crouch, Gautam Dutt, Eric Larson, and Ellen Thomson.
In
particular,
Margaret and Gautam have provided countless hours of editorial
and
production assistance, and unflagging support in this long endeavor.
To all of
these people I give a heartfelt thanks.
Those mistakes that
remain in the
text are mine alone and somehow remain despite all the
patient
editorial assistance that I have received.
Similarly, several
illustrations
of lower quality remain -- they are due to my shaky hand and
somehow
remain despite the professional assistance available to me.
I
hope the
reader will understand the underlying themes of this work despite
these
shortcomings.
I would also
like to thank my sister, Hannah, for first making me aware of
the problems
in developing countries. This book is
testimony to the
profound
impact a simple trip to visit her in Senegal in 1972 has had on
my career.
Finally, I
would like to thank my wife, Emory, for her love, patience, and
understanding
during the long months while what was intended to be a 50-page
technical report
turned into a 300-page book.
Sam Baldwin
November
1986
TABLE OF
CONTENTS
Acknowledgements
Table of
Contents
I.
INTRODUCTION AND OVERVIEW
II.
FUELWOOD, CHARCOAL, DEFORESTATION, AND
STOVES
Fuelwood
Charcoal
Environmental Impacts
Economics and Policy Options
III. STOVE
DESIGN
Conduction
Convection
Radiation
Combustion
Other Aspects of Stove Efficiency
IV.
STOVE CONSTRUCTION
Construction Options
Template Design: Cylindrical Stoves
Metal Stove Production
Fired Clay Stove Production
V.
STOVE TESTING
Laboratory Tests
Controlled Cooking Tests
Production Tests
Field Tests
Marketing Tests
VI.
CHARCOAL FUELED SYSTEMS
Charcoal Stoves
High Temperature Furnaces
APPENDIXES
A. Conduction
B. Convection
C. Radiation
D. Combustion
E. Heat Exchangers
F. Financial Analysis
G. Statistical Methods
H. Testing Equipment
I. Units and Conversions
J. Institutions
NOTES,
REFERENCES, AND FURTHER READING
INDEX
CHAPTER I
INTRODUCTION
AND OVERVIEW
Developing
countries are now suffering serious and increasingly rapid
deforestation.
In addition to environmental degradation,
loss of forest
cover removes
the wood energy resources on which traditional rural
economies are
based. In response to the increasingly serious shortages,
programs to
conserve fuelwood supply and to expand fuelwood production
have
multiplied, but have frequently been ineffective due to a lack of
understanding
of the economic, political, social, and technical complexities
of these
problems.
The primary
intent of this book is to resolve some of the technical
problems of
conserving fuelwood supply(1). This is
done by using the
principles of
modern engineering heat transfer to redesign traditional
energy
technologies. As shown, this unlikely marriage of the modern and
the
traditional is a powerful tool for improving the lives of the Third
World's poor.
The book is
divided into two parts, the text and the technical appendixes.
The text is
written for generalists who need a qualitative yet detailed
understanding
of stove design and testing. The appendixes are written for
specialists
who need an introduction to the application of the principles
of combustion
and heat transfer to stove design. The two parts are combined
into a single
volume so as to emphasize the importance of technical
analysis to
stove design, development, and dissemination.
In brief, the
contents are
as follows.
______________________
(1) A
companion volume discusses policy aspects of using biomass energy
resources for
rural development (1). Stove program planning and implementation
are discussed
at length in reference (2).
Chapter II,
Fuelwood, Charcoal, and Deforestation, reviews the role of
fuelwood in
traditional societies, and the environmental, economic, and
policy
considerations of increasing deforestation and worsening fuelwood
shortages.
Although fuelwood demand is not a primary
cause of deforestation
on the global
scale, it can significantly increase pressures on
forest
resources locally, particularly around urban areas in arid regions
where the
fuelwood demand is large and the biomass productivity of the
land is
small. In turn, deforestation places an
enormous financial and
physical
burden on hundreds of millions of people in developing countries
as they
struggle to obtain vital supplies of fuel with which to cook their
food and heat
their homes.
Responses to
these problems might include tree planting programs, improved
land
management, or the importation of fossil fuels for cooking. All of
these may be
important components of any long-term strategy to meet the
energy needs
of developing countries (1). Yet in
many rural and urban
areas such
programs cannot be implemented quickly enough or are too
expensive to
overcome the rapidly growing fuelwood deficits.
Improving the
energy efficiency of biomass burning stoves potentially
offers a
highly cost-effective alternative for easing the burden of buying
fuel by urban
poor and collecting fuel by rural poor. Better stoves also
promise
important health benefits to their users by reducing smoke
emissions.
Finally, stoves may ease pressures on forests as well as help
maintain
long-term soil productivity by reducing the need to burn crop
residues and
dung.
Chapter III,
Stove Design, discusses the technical aspects of combustion
and heat
transfer as applied to improving biomass burning cookstoves(2). The
following
points are emphasized:
o
Conduction processes in the stove require
the stove to be as lightweight
as possible to minimize stored heat in the
walls and, where
possible, to be lined with lightweight, high
temperature insulants to
reduce heat loss to the outside. Their
light weight and easy transportability
allow centralized mass production with
distribution through
existing commercial channels or
decentralized mass production with
distribution by informal sector artisans.
______________________
(2)
"Biomass" as used in this book refers to raw or unprocessed biomass
fuels such as
wood, agricultural wastes, or dung. In
contrast, fuels such
as charcoal,
ethanol, methanol and others that are derived from raw
biomass are
termed "processed biomass" fuels.
"Cookstoves"
(or simply "stoves") refers primarily to stoves designed for
heating
water. Uses could include domestic,
restaurant, or institutional
scale cooking
(boiling) or hot water heating; commercial and industrial
uses such as
beer brewing, cloth dyeing, or food processing (boiling); and
others.
It does not refer to stoves for frying foods
or to woodburning
ovens, nor
does it apply to space heating stoves, although many of the
same considerations
will generally be applicable.
Introduction
o
Convection processes in the stove require
very precise control over the
stove dimensions and precise matching of
the stove to the pot. The
high degree of precision needed
necessitates mass production based on
standard templates.
Thus, because
of fundamental principles of heat transfer, site-built or
massive
stoves are unlikely to show acceptable performance; mass produced
lightweight
stoves with carefully optimized and controlled dimensions are
much
preferred.
In addition,
combustion and radiation heat transfer processes are discussed
in Chapter
III and opportunities are presented for
further research to
increase
efficiency and reduce emissions.
Chapter IV,
Stove Construction, applies the technical findings of Chapter
III to the
practical aspects of actual stove construction. Template design
and step by
step production are described in detail for several metal and
fired clay
stoves recently developed and now being disseminated in West
Africa.
Additionally, suggestions are made for a
variety of other stove
configurations
that may better suit conditions in other areas.
In Chapter V,
Stove Testing, step-by-step procedures are recommended for
testing stove
prototypes and establishing a rudimentary stove industry. In
brief,
laboratory and controlled cooking tests are used to select particularly
promising
prototypes. From these tests, standard
templates are
developed
that conform to the local pot sizes and shapes. A production
test is then
run producing 50, 100, or more stoves for each of the most
popular pot
sizes. During this production test, a
detailed analysis is
performed of
the costs, the problems encountered, and potential improvements
in the
production method.
Some of the
stoves produced are distributed on a short-term, temporary
basis to
selected families for field testing to determine both their
acceptability
and their actual performance.
Another
portion of those stoves is put on display in local commercial
outlets and
sold on a commission basis. Such
simultaneous marketing may
allow some
indirect feedback on how neighbors of the selected families
perceive the
stoves' potential. Marketing techniques
such as radio and
newspaper
advertising, billboards and other publicity, and public demonstrations
at social
centers, schools, religious centers, and elsewhere
should also
be attempted. As interest develops, the
stove promoter can
gradually
withdraw, leaving the stove producer in direct contact with the
various
commercial outlets. If interest does
not develop, modifications
will be
necessarily based on the field and market surveys and any other
information
that is available.
It must be
emphasized that detailed, methodical testing of prototype
stoves;
careful financial and statistical analysis of the results; and use
of these
results to improve subsequent prototypes is crucial if improved
stoves are to
be disseminated successfully and widely. In some areas the
testing
prescriptions provided will need to be modified; in other areas
they will
need to be completely reworked. But
everywhere, careful,
methodical
testing and use of the results are crucial to understanding and
overcoming
obstacles to good stove performance and acceptability.
Chapter VI
briefly examines improvements in Charcoal Fueled Systems such
as stoves and
high temperature furnaces that may save large amounts of
fuelwood when
developed.
Technical
Appendixes document the text in detail and provide the technical
reader the
foundation for more detailed understanding.
Topics discussed
include
conductive, convective, and radiative heat transfer processes;
principles of
combustion; air to air heat exchanger design; and techniques
for financial
and statistical analysis of test data.
Analytical and
numerical
solutions to heat transfer equations are described in detail and
the results
are presented in the text. Extensive
references are noted for
those who
wish to do more detailed work and a list of institutions is
provided for
contact with ongoing programs.
The specific
technologies discussed in this book are by no means finalized:
rather they
are beginnings. Each has certain
advantages, such as
fuel
efficiency or safety, compared to traditional forms, but also brings
with it
certain disadvantages such as reduced flexibility or increased
cost. Whether
or not the improved technology is adopted in any area will
depend on the
local fuel supply, the local economy, and a host of other
factors.
Further, the response will be dynamic,
changing as conditions
change.
As biomass energy resources decrease,
however, the demand for
more fuel
efficient technologies must grow.
Adaptation and further
development
of the technologies described here can provide the vital
energy
services needed by the world's poor in an increasingly resource
limited
world.
Similarly,
this book is by no means a completed study but rather is an
introduction
to the application of modern scientific analysis to traditional
technologies.
In the examples discussed below, when modern engineering
heat transfer
is applied to traditional energy technologies, new
technologies
are developed with enormous potential to improve the lives of
the world's
poor. Combined with modern mass production techniques that can
carry the
fruits of a single dedicated engineering effort to the entire
world, this
enormous potential can be realized. There is not time to
waste.
CHAPTER II
FUELWOOD,
CHARCOAL, DEFORESTATION, AND STOVES(1)
Ever since
people learned to control fire they have been actively deforesting
their
environment, initially using fire to aid in the hunt and
later to
clear land for agriculture. Tierra del
Fuego or "Land of Fire"
was so named
by Magellan in 1520 because of the numerous fires he saw
there set by
indigenous South Americans. Tropical
savannahs and temperate
grasslands
are, in large part, a consequence of such repeated burnings.
An estimated
half of the world's deserts were similarly created (1).
Recorded
history has numerous examples of such deforestation. Crete, once
heavily
forested, suffered severe wood shortages by 1700 BC due to the
demands of a
growing population. Cyprus provided the bronze needed by the
ancient
Greeks for weaponry. Wood shortages are a likely cause for the reduction
in bronze
smelting there by 1300 BC which forced rationing on the
Greek
mainland and weakened the Mycenaeans to outside attack.
Aristotle
and Plato
both documented the destruction of forests in Greece and the
consequences.
The Romans were forced to import wood from
North Africa,
France, and
Spain to keep their industries, public baths, and military
operational.
England suffered severe deforestation in
many areas during
her early
industrial period -- citizens even rioted over rising wood
prices --
until the transition to coal was made (2,3).
Today, the
world's forests face unprecedented pressures. While potentially
a renewable
resource, forests are disappearing faster than they are being
replaced. The
United Nations Food and Agriculture Organization estimates
that forests
are being lost to agriculture, grazing, commercial timber,
uncontrolled
burning, fuelwood, and other factors at a rate of more than
11 million
hectares per year, with 90% of the cleared land never replanted
(4,5).
_____________________
(1) The
author would like to acknowledge the assistance of Timothy Wood
in preparing
portions of this chapter.
As forests
disappear, the financial and physical burden of obtaining wood
fuel for
cooking and space heating increases for the world's poor.
In
response,
many turn to crop wastes and dung as an alternative, but one
that has
potentially serious consequences for future soil fertility (6,7).
This is not a
small or isolated problem. Nearly two
million metric tons
(tonnes) of
wood, charcoal, crop wastes, and dung are burned daily in
developing
countries, or approximately one kilogram each day for every
man, woman,
and child. Although the energy obtained represents only about
10% of the
energy consumed worldwide, it is over half the energy consumed
in some 50 to
60 developing countries and is as much as 95% of the
domestic
energy used there (6-9).
Biomass fuels
thus play a critical role in the economies of the developing
countries.
In this chapter the supply and demand of
these fuels, their
production
and economics, and the environmental consequences of their use
are reviewed
in detail. Although the extensive
statistics presented are
themselves
unemotional, one cannot be unemotional about the awesome toll
on human
well-being that they represent. The
high cost of fuelwood
represents
food, medicine, and clothing that the urban poor must forego.
The long
distances walked and heavy loads carried by the rural poor
foraging for
fuel represent time and labor better spent growing food or
producing
goods for sale in village markets. The
large amounts of smoke
emitted by
traditional stoves represent the discomfort and disease that
this smoke
can cause the user. Only in such a broad context can the full
impact of
traditional fuels and stoves on human life and well-being be
appreciated.
FUELWOOD
The total
global annual growth of forest biomass has been variously
estimated to
be about 50 times annual wood consumption and five times
total annual
energy consumption including fossil fuels (Note 142)(2) (10).
Despite the
large average global supply, there are acute and growing
shortages of
fuelwood regionally and locally. Some regions, such as Asia,
have very
little per capita forest growing stock (Note 143).
Within
regions, some
countries are well endowed with biomass energy resources,
and others
have totally inadequate supplies, (Table 1); and within
countries
themselves, there are similar local abundances and shortages.
Zaire, for
example, consumes only 2% of its sustainable yield of forest
biomass but
has serious deforestation around Kinshasa (12).
In areas
where forest resources cannot meet the demand, crop residues and
animal dung
are marginally sufficient substitutes at best. In Bangladesh,
for example,
crop residues and animal dung can supply about 300 watts per
capita (Table
1). This is barely enough to meet minimum needs.
_______________________
(2) So as to
not overburden the text yet still provide the reader with
detailed
information, a number of Tables are given as Notes beginning on
page 251.
TABLE 1
Biomass Energy Resources in Selected
Developing Countries
Sustainable
Yield in Watts/capita of
Population
Crop
Animal
Country
(millions)
Wood Residues
Dung
Congo
1
18100 35
n.a.
Brazil
116
11100 257
507
Zaire
30
4300 29
35
Argentina
27
3900 793
1270
Thailand
48
1170 295
124
Nepal
14
666 225
412
Burkina Faso
7
317 162
231
India
694
222
174 200
Bangladesh
89
63 136
162
China
970
n.a. 216
108
Adapted from reference (20) ; n.a. --
not available
Estimates
such as these are, of course, only very crude approximations.
As these
traditional fuels do not usually move through monitored commercial
markets,
estimates of their production and use can only be made by
detailed
measurements at the locale in question.
Further, there is
considerable
confusion in the literature over the units used to measure a
given
quantity. For example, foresters
generally use volumetric units to
measure wood
but sometimes fail to specify whether it is in units of solid
cubic meters
or stacked cubic meters (steres). Nor
is the species and
density
specified. Note (144) gives very rough
equivalences between the
two
volumetric units for different classes of harvested wood. Similarly,
charcoal is
usually measured by volume, but its energy content is determined
by its mass,
which in turn is determined by the species from which
it was
carbonized (14), the temperatures at which it was carbonized, i.e.,
its residual
volatile content (15), and its packing density.
When
estimates of energy content are based on weight, the preferred
method, it is
similarly vital to know the moisture content of the fuel and
whether the
weight is on a wet or dry basis (see Chapter III).
Estimating
biomass energy resources should therefore be done by direct
measurement.
Forest resources can be measured by
estimating standing
volumes or by
cutting an area and making a direct weight or volume
measurement
(16-19). Crop residues from the same species can vary widely
by soil type
and rainfall as shown in Note (145) and similarly should be
directly
weighed. Growth rates can be estimated
by numerous repetitions
of such
measurements on comparable, adjacent samples over a period of
time.
Finally, where animal dung is, or could be, used as an energy
resource, it,
too, should be measured directly.
Estimates of dung
production
rates are given in Note (146).
Calorific values for a number
of different
biomass fuels are given in Appendix D.
Biomass
energy resources have been estimated for a variety of local,
national, and
regional cases as described in references (4,7,9,13,20-28).
Fuelwood
Demand
Numerous
estimates of biomass fuel demand have been made on the local,
national, and
regional scale (29-59). The rate of
energy use by the
typical
villager is usually in the range of 200-500 watts per person and
can vary
dramatically with the season, climate, and general availability
of various
fuels. Energy survey results are given for nearly 40 towns and
villages in
Note (147). Much of this energy is used for domestic cooking
(Tables
2,3,6) and these values are much higher than the amounts of energy
used in
developed countries for cooking (Table 4).
This is due to the
inefficiency
of traditional fuels and stove technologies as well as
changes in
diet and lifestyle that are possible with higher incomes.
Globally,
biomass fuels are the principal source of cooking energy for
most
developing countries (Table 5).
Additionally, they provide energy
for household
needs such as heating bath water, ironing, and other uses.
Though
perhaps atypical, 60% of domestic wood consumption in Bangalore,
India, is
used to heat bath water (45).
Although
their principal use in developing countries is domestic, biomass
also fuels
much of the industry. As seen in Tables 7 and 8, biomass fuels
two-thirds of
Kenyan industry and commerce and it is used for such things
as beer
brewing, blacksmithing, crop drying, and pottery firing.
TABLE 2
Total Power Consumption,
Ungra, India
Watts/Capita(*)
Source\Use
Agriculture
Domestic Lighting
Industry
Total
Human
7.26
17.08
-- 4.52
28.86
Man
(5.11)
(6.01) --
(3.92)
(15.04)
Woman
(2.15)
(8.70) --
(0.56)
(11.41)
Child
--
(2.36) --
(0.04)
(2.41)
Animal(**)
12.0
--
-- 1.11
13.11
Firewood
--
222.8
--
36.85 259.7
Agro-waste
--
23.2
-- --
23.2
Electricity
3.18
--
1.17 0.37
4.72
Kerosene
--
0.19
6.88 0.97
8.04
Diesel
0.04 --
--
-- 0.04
Coal
--
--
-- 1.41
1.41
Total
22.5
263.3
8.05 43.23
339.
(*) Based on
a total village population of 932 people in 149 households
(**) Provided
by 111 bullocks, 143 cows, 93 calves, 113 buffalo and 489
sheep and goats.
Reference
(50)
Estimates of
the energy intensity of commercial uses vary widely, but all
indicate
substantial amounts of fuelwood used and often at very low
efficiencies.
One stacked cubic meter of wood, for
example, is required
to cure 7-12
kg of tobacco leaf. The efficiency of
tobacco drying barns
in Tanzania
has been estimated to be as low as 0.5% (49).
Tobacco curing
uses 11% of
all fuelwood in Ilocos Norte, Philippines and 17% of the
national
energy budget in Malawi (34,39,47,56,59).
Tea
processing requires roughly 9.5 GJ or 500 kg of dry wood to produce 30
kg of dry tea
leaves from 150 kg of green leaves (45,47).
Fish smoking/
drying is
variously estimated to require from 0.25 kg (39) to 3 kg (40) of
fuelwood per
kilogram of fish dried (47,59).
Brickworks require roughly
one stacked
cubic meter of fuelwood to fire 20-25 pots (39) or 1000 bricks
(59).
In Bangalore, dyeing a tonne of yarn
requires some 8.3 tonnes of
fuelwood;
bakeries use 0.58 kg of fuelwood per kilogram of traditional
bread
produced (45). In Tanzania, beer
brewing requires a stacked cubic
meter to
produce 180 liters (59), and the brewing industry in Ouagadougou
uses 14% of
the total fuelwood used (60). Other
major users include
institutional
kitchens, wood processing (45), and sugar production, for
which the
bagasse itself is used. Overall,
biomass fuels supply up to 40%
of the
industrial energy used in Indonesia, 28% in Thailand, 17% in
Brazil, and
similarly large fractions in many other countries (9)(3).
TABLE 3
Domestic Power Consumption,
Taruyan, West Sumatra
Watts/Capita
Labor(*)
Firewood
Bagasse Kerosene
Total
Cooking
8.6
181. 2.9
--
193.
Water
Collection 2.6
--
-- --
2.6
Laundry
2.0
-- --
-- 2.0
Wood
Collection 1.9
--
-- --
1.9
Delivering
Food 0.6
-- --
--
0.6
Lighting
--
-- --
52.1
52.1
Total
15.7
181.
2.9
52.1 252.
Percentage
6.2%
71.9% 1.1%
20.7%
100.%
(*)Calculated
at 1.05 MJ/man-hour; 14.9 MJ/kg firewood; 37.7 MJ/liter
Kerosene; 9.2
MJ/kg bagasse.
Reference
(58)
_________________________
(3)A variety of units, GJ (giga-joules), kg., [m.sup.3] ,
tonnes, etc. , are
used here to
correspond to the literature rather than using a single set
of units --
preferably GJ and watts. Conversion
tables for all these
units are
given in Appendix I, approximate stacking factors for wood and
charcoal are
given in Notes (144,149), and calorific values are given in
Appendix D.
The author regrets the inconvenience.
TABLE 4
Power Consumption for
Cooking
Country
Fuel
W/cap
Brazil
LPG
55
Brazil
Wood
435
Canada
Gas
70
Cameroon
Wood 435
France
Gas
55
West Germany
Gas
30
Guatemala
Propane
50
Guatemala
Wood
425
India
Kerosene
50
India
Wood
260
Italy
Gas
55
Japan
Gas
25
Sweden
Gas/kerosene
40
Tanzania
Wood
590
United States
Gas
90
References (63,64)
TABLE 5
World Population by Principal
Cooking Fuel, 1976
(millions of
people)
Commercial
(fossil) Dung and
Total
Energy
Fuelwood Crop Waste
Africa South
of Sahara 340
35
215 90
India
610
60
290 260
Rest of South
Asia 205
25
95 85
East
Asia-Developing Pacific 265
95
110 60
Asia,
Centrally Planned
Economies
855
190 435
230
Middle East,
North Africa 200
105
35 60
Latin America
and Caribbean 325
230
85 10
North America
- OECD Pacific 365
365
0 0
Western
Europe 400
400
0 0
European,
Centrally Planned
Economies
340
340 0
0
Total
3905
1845
1265 795
Reference
(11)
TABLE 6
Energy Consumption
in Kenya
Percent of National
Total(*) by End-use
Non-
Biomass
Traditional
Fuel
Wood
Charcoal Other
Urban
Household
Cooking/Heating
0.8%
1.0%
3.3% --
Lighting
0.6
-- --
--
Other
0.2
-- 0.5
--
Rural
Household
Cooking/Heating
0.2 45.3
2.8
2.7%
Lighting
1.1
-- --
--
Industry
Large
8.6
5.3 0.3
--
Informal
Urban --
0.1
0.6 --
Informal
Rural --
9.1
0.1 --
Commerce
0.6
0.5 0.1
--
Transportation
13.7
-- --
--
Agriculture
2.5
-- --
--
Total
28.4%
61.3%
7.6% 2.7%
(*)Total
National Energy Consumption = 332 million GJ
Per Capita Power Consumption = 658 W
Reference (24)
TABLE 7
Annual Consumption of Fuelwood
and Charcoal in Kenya
by Rural Cottage
Industries, Watts/Capita
Fuelwood
Charcoal
Industry
W/cap
W/cap
Brewing
33.9
--
Brick firing
1.9
--
Blacksmithing
--
1.9
Crop Drying
1.3
--
Fish Curing
0.6
--
Tobacco Curing
1.3
--
Butchery
7.6
1.9
Baking
4.1
--
Restaurants
5.4
1.3
Construction Wood
15.9
--
Total
72.
5.1
Reference (24)
Biomass fuels
are crucial to the economies of most developing countries.
Note (148)
lists 60 countries in which biomass fuels provide 30-95% of the
total energy
used. The energy these fuels provide,
however, is only a
fraction of
that used by fossil fuel based economies (8,31).
In the
developed
world, average per capita energy use is about 6 kW while in
Africa and
Asia it is barely one tenth of this (8); in North America,
energy use is
over 10 kW, while in Africa it is about 450 W (8,31).
With these
rates of biomass energy use and supply there is a serious and
growing
shortage of fuelwood in many areas. The
UNFAO has estimated that
the number of
people suffering an acute shortage of fuelwood will increase
from about
100 million in 1980 to over 350 million in the year 2000 (Table 9).
Such
shortages increase costs for urban dwellers, lengthen foraging
for fuel by
rural dwellers, and rob the soil of nutrients as people switch
to crop
wastes and dung.
TABLE 8
Fuelwood Consumption
in Kenya
by Large Industry,
Watts/Capita
Industry
W/cap
Tea (average)
8.9
Tobacco
2.5
Sugar
1.6
Wood Processing
9.5
Wattle
1.3
Clay Brick
1.0
Baking
9.5
Total
34.3
Reference (24)
TABLE 9
The Fuelwood Shortage in
Developing Countries
(millions of people
affected)
1980
2000
acute
deficit
acute deficit
scarcity
scarcity
Africa
55 146
88
447
Near East &
North Africa --
104
-- 268
Latin America
15
104 30
523
Asia & Pacific
31
645 238
1532
Total
101
999 356
2770
Reference (6)
TABLE 10
Fuelwood in World Power
Consumption (1978)
Fuelwood
Commercial
Percent
Population
Consumed
Power Consumed
wood/total
millions
per capita
per capita
World
4258
110 W 1913
W 5.4%
Developed
market
775
21 5946
0.3
planned
372
73
5118
1.4
Developing
Africa
415
254 185
58.
Asia
2347
101 508
17.
Latin
America
349 232
1028
18.
Reference (8)
CHARCOAL
Charcoal is
produced by heating wood in the absence of oxygen until many
of its
organic components gasify, leaving behind a black porous high
carbon
residue. The charcoal thus produced
retains the same shape as the
original wood
but is typically just one fifth the weight, one half the
volume, and
one third the original energy content.
A more precise
relationship
is given in Note (149).
The charcoal
has a calorific value of 31-35 MJ/kg, depending on its
remaining
volatile content, compared to 18-19 MJ/kg for oven-dry wood.
Table D-2
illustrates how the temperature history of the carbonization
process
affects the volatile content and calorific value of the resulting
charcoal.
There are two
different classes of carbonization equipment, kilns and
retorts.
Kilns burn part of the wood charge being
carbonized to provide
the heat
necessary for the carbonization process.
Retorts use a separate
fuel source
to provide heat and thus can conserve the higher quality
product being
carbonized by using a lower quality fuel such as twigs and
branches for
the heating. An extensive review is
given in reference (156).
The most
widespread system used in the developing world is a kiln made of
earth.
In this case the wood is stacked compactly
either in a pit or on
the flat
ground, covered with straw or other vegetation, and, finally,
buried under
a layer of soil. It is ignited with
burning embers introduced
at one or
more points at the bottom of the stack.
The task of the
charcoal-maker
throughout the ensuing "burn" is to open and close a
succession of
vent holes in the soil layer to draw the fire evenly around
the wood
stack, heating the wood while burning as little of it as possible.
Other systems
in use include brick kilns, which are used extensively
in Brazil
(66,67).
The size of
the kiln can be as much as 200 stere (68) and the energy
efficiency of
the conversion process is variously given as 15% in Tanzania
(47), 24% in
Kenya with an additional loss of 5% of the charcoal itself
during
distribution (24), 29% in Senegal (69) and Ethiopia (70), and over
50% in Brazil
with brick kilns (67). Advanced retorts
are claimed to be
capable of
achieving 72% energy efficiencies in converting wood to charcoal
if there is
complete recovery of all of the gaseous by-products (67).
The large
variation in reported kiln efficiencies may be due in part to
confusion
about units -- energy, weight, or volume, and wet or dry basis.
When
side-by-side tests are done, energy efficiencies are typically in the
30-60% range
as indicated in Table 11 (71,72). The
relative economic
performance
of a few types of kilns is given in Table 12.
The poor economics
of the
earthen kiln listed in Table 12 may be due to the very small
size
studied. Others have found traditional
earthen kilns to have fairly
high
performance and a good financial return with relatively little labor
(71).
Their disadvantages, however, include a
variable yield and quality,
slow burns,
and seasonal availability (not during the rainy season).
No
matter what
system is used, however, producing charcoal results in a very
large net
energy loss. In terms of conserving
forest resources, it is
always better
to use wood rather than first converting it to charcoal.
Charcoal
Transport
It has been
frequently argued that it is cheaper and more efficient to
transport
charcoal than wood because of its higher energy content per unit
mass.
As shown below, however, the amount of
energy, whether in the form
of wood or
charcoal, that can be carried per truckload is about the same.
As transport
costs are primarily due to vehicle depreciation and maintenance,
the cost of
hauling wood or charcoal is about the same per unit
of energy
carried (150).
By assuming
transport costs at a fixed US$0.10 per metric ton-kilometer,
Earl found
that it was cheaper to transport energy in the form of charcoal
than in the
form of wood for distances greater than 82 km (13).
Chauvin
similarly
used a fixed cost per ton-km. in his analysis of the economics
of
transporting charcoal from the Ivory Coast to Burkina Faso by rail (60)
Expressing
transport costs in terms of ton-km's is a standard practice in
aggregated
transportation statistics, but is not applicable in this
situation.
Most of the energy is used to move the
vehicle itself, to
overcome wind
resistance, internal friction and so forth.
Thus, an empty
truck uses
nearly as much energy as one that is full.
A linear regression
on data
presented in reference (73) shows that the energy intensity of
transport by
tractor-trailers in the USA is related approximately to the
payload for
the range 8-25 metric tons by the equation
E = 23.6/M + 0.476
where E is
the energy intensity in MJ per metric ton-km the load is moved,
and M is the
mass of the load in metric tons.
Transport is more often
limited by
volume than by weight and this is particularly true in the
developing
world where vehicles are usually filled to overflowing.
In
this case of
volume limited transport, Table 13, 13% more energy can be
transported
per truckload of wood than of charcoal at a cost of a 21%
increase in
fuel use.
Fuel costs,
however, are only a small part of the total transport costs
and at least
in some cases, do not substantially increase even on unimproved
roads
(74). Maintenance and repair of
vehicles is a large factor
(74) and
vehicle depreciation and labor are even larger (75).
TABLE 11
Energy Efficiencies of Assorted
Carbonization Systems
Thailand, 1984
Total
Charcoal as
Charcoal Number
Volume
Energy % of
Production of
[m.sup.3]
Dry Wood
Rate kg/hr Trials
Brick Beehive
1 8.3
61%
11.1 3
Brick Beehive
2 2.0
63
5.6 35
Brazilian,
modified 8.3
55
10.7 2
Mark
V(2) 2.6
43
10.1 7
Mud Beehive
3 2.2
56
5.1 27
Single
Drum 0.2
38
5.9 7
Earth
Mound 0.7
51
4.6 5
Reference
(72). Also see (72) for data on 12 other types of kilns.
TABLE 12
Charcoal Production
Economics
Thailand, 1984
Per Burn
Wood(*)
Capital(**)
Labor(***) Charcoal
Investment
US$/tonne
Brick Beehive
1 $52.
$1.67
$9.00 $65.
Brick Beehive
2 15.
0.66
3.70 75.
Brazilian,
modified 54.
1.13
9.80 71.
Mark
V(2) 33.
3.15
4.70 90.
Mud Beehive
3 16.
0.17
4.10 74.
Single
Drum 1.80
0.18
1.95 195.
Earth
Mound 3.70
--
2.35
114.
(*)Wood costs
US$8.30/stere; (**)Interest rate is 15%; (***)Labor is
US$0.40/man-hr.
Reference
(72). Also see (72) for data on 12
other types of kilns.
TABLE 13
Energy Required to Transport
Wood and Charcoal
Factor
Wood
Charcoal
Assumed
volumetric gravity
0.7 0.33(a)
Assumed
packing density
0.7 0.7 (b)
Effective
volumetric gravity 0.49
0.23
Energy
content per truckload 390.
GJ(*) 345. GJ (c)
Weight per
truckload 24.5
MT(**) 11.5 MT (d)
Transport
energy per truckload-km
35.3MJ/km 29.1 MJ/km
Transport
energy per km/energy
content of
load
91x[10.sup.-6]
84x[10.sup-6]
(*)GJ is a
gigajoule or 1 billion joules; (**)MT is a metric ton, 1000 kg
a)
Based on (14).
b)
For wood based on (13). Charcoal may have a
higher or lower packing
density depending on its size and whether
or not it is bagged for
transport.
It is normally bagged for transport.
c)
Assumed calorific value for wood, 16 MJ/kg;
charcoal, 30 MJ/kg;
both including moisture.
d)
Based on a payload volume of 50
[m.sup.3]. This is less than a standard
tractor trailer, but was chosen so as to
remain within the limits
of the correlation of weight to transport
energy, yet correspond
to the case for most developing countries
of volume limited transport
for either wood or charcoal.
TABLE 14
Transport Costs of Wood
and Charcoal
Percent of
Total
Wood Charcoal
Labor and management
12%
12% (a)
Fuel
18
15 (b)
Maintenance and repair
40
30 (c)
Licenses and tolls
1
1
Vehicle depreciation
42
42
Total costs
113
100
Energy hauled
113
100 (b)
a)
From reference (75) using charcoal as the
baseline.
b)
From Table 21.
c)
Estimated from reference (75) data on tire
depreciation and
vehicle repair charges assuming that these
costs increase proportionately
to the total vehicle weight.
When these
costs are considered, Table 14, the cost of hauling energy,
whether in
the form of wood or charcoal, is virtually identical.
In
practice,
factors such as vehicle size, labor and fuel costs, part-load or
back-haul of
goods, and many others will complicate this analysis.
When
production costs are included, charcoal is more expensive than
fuelwood.
These costs are reflected in their relative
prices: the price
per GJ of
charcoal is typically twice that of fuelwood (76).
Charcoal
Demand
Despite its
higher price, charcoal is a very popular fuel, particularly in
urban areas
where people have a cash income.
According to a 1970 report
from
Thailand, 90% of the wood cut for urban markets was converted into
charcoal
(34). In Tanzania that figure is 76%,
with 10-15% of all wood
cut converted
to charcoal (40,59). In Senegal, 15% of
all wood cut is
converted to
charcoal for Dakar alone, transported to Dakar from as far as
600 km away,
and used there by 90% of the households at a rate of 100
kg/person-year
(77,78). In Kenya, 35% of the wood cut
is converted to
charcoal
(24).
Although
traditional charcoal stoves have an efficiency (15-25%) somewhat
higher than
the open wood fire (15-19%), this does not compensate for the
drastic
energy loss in the initial conversion from wood (79,80).
There are a
variety of reasons for this popularity despite high cost and
energy
inefficiency. Unlike some wood species
that must be used within as
little as a
month of drying to avoid significant losses to termites,
charcoal is
impervious to insect attack (21). It
can, therefore, be
prepared far
in advance of, for example, the rainy season when other fuels
are
unavailable. Even more important is
that charcoal is a very convenient
fuel to
use. Charcoal is nearly smokeless.
Cooking can be done indoors
in relative
comfort without blackening the walls with soot.
Metal pots
stay
relatively clean, and there is no smoke irritation to eyes or lungs.
Although
there can be a high output of dangerous carbon monoxide, which is
a health
hazard in poorly ventilated kitchens, this does not cause as
obvious
discomfort to the user. Additionally,
once it is lit, a charcoal
fire needs
little further attention from the cook, while a wood fire
requires
frequent adjusting of the fuel.
The
willingness of urban dwellers to purchase expensive charcoal should
thus
encourage designers of improved stoves who are attempting to eliminate
smoke, ease
the drudgery of cooking, and further reduce fuel costs.
At the same
time, it should serve as a warning to those who pay attention
only to fuel
efficiency.
Charcoal is
also extensively used commercially. In
Brazil, some 19
million cubic
meters of charcoal were used during 1983 to produce pig
iron, 2.5
million were used to produce cement, and 600,000 were used for
metallurgy.
Overall, about 18% of the energy used in the
Brazilian steel
industry is
from charcoal. About 17% of this charcoal
was generated from
plantations
(43,67,82).
Large amounts
of charcoal are traded internationally as well.
In 1981,
Indonesia,
Thailand, and the Philippines each exported 44-49 thousand
tonnes of
charcoal. Large importers include
Japan, with 52,000 tonnes,
and Hong
Kong, with 23,000 tonnes (65).
ENVIRONMENTAL
IMPACTS
There is now
rapid and increasing deforestation around the world.
The
UNFAO (5,83)
has estimated total annual global deforestation at about 11.3
million
hectares (Table 15). Others have
estimated it to be as high as 20
million
hectares and more per year (7). Among
the causes are the following.
Shifting
agriculture damages or destroys about 0.6% of tropical
forestland
annually and accounts for some 70% of forest loss in Africa
(84).
Opening pastureland to grow beef for export
annually clears some 2
million
hectares per year in Latin America (85-87).
Commercial timber
operations
clear roughly 0.2% of tropical forestland annually (84), and
timber access
roads open the areas to farmers leading to additional
degradation
(87). The Ivory Coast, for example, is
losing some 6.5% of its
forests
annually (5,83). Finally, uncontrolled
burning is believed
responsible
for the creation of much of the world's savannah and grassland
(1,88,89).
Such brushfires in the African grasslands
burn more than 80
million tons
of forage annually, cause volatilization of organic nitrogen,
and allow
excessive leaching of valuable salts (90).
This may be particularly
damaging in
much of the Sahel where growth is already strongly
limited by
the small available quantities of nitrogen and phosphorus (91).
The use of
fuelwood increases pressures on forest biomass and can lead to
local
deforestation (12,88), particularly in arid regions around urban
areas where demand
is high and biomass growth rates are low.
Generally,
rural
subsistence farmers cause relatively little damage to forests as
they take
only small limbs, etc., and these often from hedgerows or from
near their
farmlands. For example, in Kenya, trees
outside the forest
supply half
the wood demand (37); in Thailand in 1972, 57% of the wood
consumed came
from outside the forests (40). In
contrast, commercial
fuelwood and
charcoal operations, even relatively small-scale ones, cut
whole trees
and can damage or destroy large areas of forest.
Among the
potential impacts of deforestation are erosion, flooding,
climatic
changes, desertification, and fuelwood shortages (92-94).
Essentially
no soil or
rainfall is lost from naturally forested areas.
However,
when tree
cover is removed, massive amounts of soil can be washed away as
the rainfall
flows across the surface. Measurements
in Tanzania indicated
that up to
half the rainfall was lost as run-off from bare fallow (3.5[degrees]
slope),
carrying some 70 tonnes/ha of soil with it (95).
Similar impacts
have been
noted elsewhere (5,81,87,88,96,97).
Erosion
chokes downstream waterways and reservoirs with silt, making them
even less
capable of handling the increased volumes of water running
directly off
the watersheds (2,7). In 1982, flood
and erosion damage due
to clearing
India's forests was estimated to total $20 billion over the
previous 20
years. This estimate included loss of
top soil, loss of
property to
floods, and shortened reservoir lifetimes (5).
Other estimates
place the
direct costs of repairing flood damage at more than $250
million per
year (98). A general review of this
problem in India is given
in reference
(99).
As two-thirds
of all rainfall is generated from moisture pumped back into
the
atmosphere by vegetation, deforestation may cause serious climatic
change
(1,100). The surface reflectance is
also changed and may affect
climate
(1). With no shading, soil temperatures
rise dramatically and can
greatly
reduce the vital biological activity in the soil (87,101).
Following
deforestation, overgrazing and trampling can quickly destroy the
grass
layer. Without the protection of ground
cover, the soil receives
the full
force of pounding raindrops, bringing clay particles to the
surface and
causing surface hardening and sealing that seeds cannot
penetrate
(102,103). The end result is often
desertification. During the
past fifty
years, an estimated 65 million hectares of once productive land
have thus
been lost to desert along the southern edge of the Sahara alone
(104,105).
Additional data for Africa are given in
references (90,106).
As forest
resources are lost, whether to agriculture, timber, brush fires,
or as
fuelwood, villagers are increasingly forced to use lower quality
fuels such as
crop wastes and dung to meet their minimum needs for cooking
and other
purposes. Globally, an estimated 150 to
400 million tonnes of
cow dung are
now burned annually. The burning of
each tonne of dung
wastes enough
nutrients potentially to produce an additional 50 kg of
grain.
The cow dung now burned in India wastes
nutrients equal to more
than
one-third of the chemical fertilizer used (7).
Increasing
use of agricultural residues for fuel may cause serious damage
to
soils. Organic matter in soils provides
most of the nitrogen and sulfur
and as much
as half the phosphorus needed by plants.
It increases the
cation
exchange capacity of the soil, binding important minerals such as
magnesium,
calcium, potassium and ammonium that would otherwise be leached
away.
It buffers the pH of soils, and it improves
the water retention and
other
physical characteristics (151).
TABLE 15
Estimated Average Annual Rate
of Deforestation of
Tropical Forests, 1980-1985, in
Millions of Hectares
and Percent of Total
Standing Forest
Tropical
Tropical
Tropical Total
Category
America
Africa
Asia (76 countries)
Closed
forest
4339
1331 1826
7496
(0.64%)
(0.62%)
(0.60%) (0.62%)
Open
forest 1272
2345
10 3807
(0.59%)
(0.48%)
(0.61%) (0.52%)
All
forests 5611
3676
2016 11303
(0.63%)
(0.52%)
(0.60%) (0.58%)
Reference
(31)
The
destruction of forests may also have serious consequences in terms of
loss of
genetic resources, loss of potential new medical products, and
others.
These are reviewed in reference (5).
The burning
of biomass fuels has serious environmental impacts due to the
smoke
released (107-112). Although there have
been numerous anecdotal
accounts of ill
health associated with indoor biomass combustion, only
recently have
systematic scientific studies of the problem begun (112).
Results to
date indicate that in village homes, indoor concentration of
carbon
monoxide, particulates, and hydrocarbons can be 10-100 and more
times higher
than World Health Organization (WHO) Standards (111).
Further,
cooks using traditional biomass burning stoves can be exposed to
far more
carbon monoxide, formaldehyde, carcinogenic benzo(a)pyrene, and
other toxic
and carcinogenic compounds than even heavy cigarette smokers.
From this it
is expected that smoke is a significant factor in ill-health
in developing
countries. The diseases implicated
range from bronchiolitis
and
bronchopneumonia to chronic cor pulmonale to various forms of cancer
(110,111).
Indeed, the WHO now cites respiratory
disease as the largest
bsex21.gif (600x600)

cause of
mortality in developing countries (112).
Table 16 lists air
pollution
emission factors for a variety of fuels and combustion systems.
Reducing and
controlling exposure to biomass fuel emissions must be a
primary
consideration in any stove program.
Further information is
available
from the East-West Center (Appendix J).
ECONOMICS AND
POLICY OPTIONS
The growing
fuelwood shortage has a variety of economic impacts on both
rural and
urban dwellers, the rural labor force, and the national economy.
For the rural
subsistence dweller, depletion of local fuelwood resources
means ever
longer foraging times. There are
numerous estimates of these
times ranging
as high as 200-300 person days per year per household in
Nepal or 7%
of all labor (22,46,98) and similarly high labor rates in
Tanzania (59)
and other countries (99). Approximate
correlations relating
foraging
distance to the local population density are easily developed by
equating the
average consumption by a population to the area required to
provide a
sustained yield, as shown in note (114).
A second example is
given in
reference (115). In arid regions with a
low biomass growth rate a
village of as
few as 500-1000 people can use up all the fuelwood within a
walking
distance. Foraging is also heavy work;
in Burkina Faso, typical
headloads
weigh 27 kg (113).
When wood
becomes scarce, crop wastes and dung are the villagers' only
alternative;
there is no cash for commercial fuels, nor do the long-term
environmental
costs of using agricultural wastes outweigh their immediate
value as
fuel. In India, it has been estimated
that a tonne of cow dung
applied to
the fields would result in increased grain production worth
US$8, but if
burned would eliminate the need for firewood worth $27 in the
market
(116,117). Some have argued that due to the relatively low efficiency
of cow- dung
in providing nutrients such as nitrogen, phosphorus,
potassium,
and zinc to the soil in a useable form, it makes better sense
to burn it
(117). This, however, ignores other
important contributions of
organic
materials to soil fertility (151).
With a high
market value for biomass fuels, the poor and landless are
sometimes
denied access to their traditional fuel sources (118).
It has
even been
reported that farm laborers in Haryana, India, formerly paid
cash wages,
are sometimes instead paid crop residues to be used for fuel
(99) -- fuel
they previously received free.
In contrast,
urban dwellers often have no choice but to purchase their
fuel.
Again, there are numerous estimates of the
financial burden this
imposes
ranging up to as high as 30% of total family income in Ouagadougou
(34), to 40%
in Tanzania (39), to nearly half in Bujumbura, Burundi (36).
During the
1970s the cost of wood and charcoal increased at a rate of 1-2%
per year
faster than other goods (76). Due to
their rapid price escalation
during the
1970s, fossil fuels are often not viable alternatives.
In
Malawi, the use
of kerosene declined 24% between 1973 and 1976, allegedly
due to higher
prices (34). Others have noted similar
impacts (71).
The use of
traditional fuels is important in stimulating the rural
economy.
The value of fuelwood and charcoal exceeds
10% of the Gross
Domestic
Product in countries such as Burkina Faso, Ethiopia, and Rwanda,
and exceeds
5% in Liberia, Indonesia, Zaire, Mali, and Haiti (76).
This
pumps large
amounts of cash into the rural economy and provides much
needed
employment to rural dwellers (Table 17).
To supply Ouagadougou with
wood during
1975, for example, required some 325,000 person-days of labor
and generated
over $500,000 in income directly and an additional $2.5
million in
income through transport and distribution (34).
In Uganda, an
estimated 16
tonnes of charcoal are produced per person-year (13).
Other
estimates are
given in Table 18 and references (71,72).
In many countries,
people in the
poorest areas, where conditions do not permit
expansion of
crop or animal production and the natural woody vegetation is
the only
resource, depend heavily on sales of firewood for their income
(34,99).
Whatever program is put in place to meet the
fuelwood shortage,
it will be
necessary to take the employment impacts into account.
Alternatives
To meet the
growing fuelwood shortage (Table 9), governments could import
fossil fuels
as a substitute; plant fast-growing trees and improve the
management of
existing forests; and develop more fuel efficient stoves and
other
woodburning equipment, among other actions.
If every
person now using fuelwood switched to petroleum based fuels, the
additional
consumption would be just 3.5% of 1983 world oil output.
The
cost of
kerosene and liquified petroleum gas (LPG) for all household needs
would be 15%
of total merchandise exports or less for Kenya, Thailand,
Zimbabwe, and
many other countries. Importing fuels
for cooking may then
be an
important response in such areas (152).
In contrast,
for Niger, Burundi, and others, a switch to petroleum fuels
for household
energy needs would absorb almost all merchandise export
earnings
(152). Efforts to stimulate use of
butane gas through subsidies
have begun in
West Africa but have proven to be a heavy financial burden
(34,119).
There is also evidence that such subsidies
benefit the wealthy
far more than
the poor. In West Sumatra in 1976, the
poorest 40% of the
population
used only 20% of the kerosene even though it was heavily
subsidized
(58). Yet without such subsidies,
petroleum fuels are beyond
the reach of
the poor. In these areas, other actions
are needed.
As a second
response, plantations of fast-growing tree species can be
developed to
provide fuel (123-126). Extensive data
on species, their
growth
patterns, and their uses are given in references (5,12,102,123,124)
Donor
agencies are now spending some $100 million per year on forestry
projects
(116), and additional large funding is provided by the national
governments
themselves. The U.N., however, has
estimated that $1 billion
per year is
needed to meet the minimum needs of the year 2000 when a
shortage of
about 1 billion cubic meters per year is expected with no
intervention
(6). To keep this sum in perspective,
however, it must be
compared to
the $130 billion per year needed for all energy sector
development
in developing countries (154).
TABLE 17
Breakdown of Fuelwood Cost
Factors for Niamey, Niger
$US/tonne(*)
Labor for cutting, bundling, and
hauling to road (roadside
price) 8.30
Labor for loading/unloading
2.80
Transport permit
.35
Transport
5.30
Cutting permit
5.50
Profit
5.50
Total
$27.75
Reference (121); (*) Assumes 450
CFA/US$
TABLE 18
Labor Requirements for the
Production of Fuel from Forest
Person-days/Hectare,
Uganda
Maximum Minimum
Fuelwood
120
50
Charcoal (portable
kilns) 210
88
Charcoal (earth kilns)
308
128
Reference
(38)
Plantations
can provide rural employment (115) of some 150-500 person-days/hectare
during the
first three years and almost twice that amount
during
harvesting (127). Additionally,
plantations and planting trees
generally can
provide very important environmental benefits.
Among these
are
stabilizing and protecting soils from wind and water erosion, providing
protection to
birds (which may eat crop-destroying insects -- or
the crops
themselves) and other animals, and providing important soil
nutrients.
These are reviewed in (155).
Monocropping
plantations, however, ignore the many traditional non-fuel
uses of
forests such as food, fiber, medicines, and others (128).
Some
fast-growing
species such as Eucalyptus, though productive and hardy, may
also deplete
ground water supplies and soils, be inedible as livestock
fodder, and
impede neighboring crop growth (5,99).
For other species,
however,
interplanting with crops can be valuable.
Acacia albida can
increase
yields of millet and sorghum by up to 3-4 times by fixing nitrogen
and by
pumping other nutrients from deep within the soil.
Additionally
it provides
large amounts of cattle fodder during the dry season
(102).
Other valuable species include the Tamarisk,
used in southern Iran
to control
salinity (129).
Some
countries have begun to develop substantial plantations.
Brazil, for
example, has
successfully planted 5 million hectares, mostly fast-growing
Eucalyptus,
for fuel and pulp since 1970 (67). In
contrast, in Tanzania
an estimated
200,000 hectares of plantation were needed in 1983 to meet
the country's
needs, but only 7300 were to be planted (47).
Substantial
progress is
being made, despite sometimes high costs -- over $1000 per
hectare in
places, yields that have sometimes been far below expectations
(127,130),
and numerous other problems (5,99,116,125,131,132,155).
In
parts of
Kenya, for example, individual woodlots are now being established
bsex25.gif (600x600)

widely
(140). In Table 19 several fossil and
renewable fuels are compared
on the basis
of their cost and the performance of the stoves used with
them.
As seen there, fuelwood is far less
expensive than petroleum based
fuels or
other renewable energy options.
Although this cost advantage
will decrease
in arid regions, it will likely still be significant.
Village
woodlots may further reduce the cost of fuelwood (Note 157-C).
Thus, wood
will be a primary energy source in developing countries for the
foreseeable
future.
As a third
response, improving the efficiency with which biomass fuels are
used could
greatly extend forest resources and at a very low cost.
In
this case,
the cost advantage of wood as a cooking fuel becomes even more
apparent
(Table 19). The importance of the
results shown in Table 19
cannot be
overemphasized. No other energy
resource comes close to the
cost
advantage of wood used in fuel efficient stoves.
Certainly, as
incomes rise
the cleanliness and convenience of higher quality fuels such
as kerosene,
LPG, or ethanol will be gladly paid for; but this is not now
a viable
option for many of the world's poor.
Thus, a significant effort
must be focused
on the development of stoves that burn wood, but do so
cleanly and
safely, with high efficiency, and that are easily controlled.
The cost of
saving energy by using an improved stove can also be compared
to the cost
of producing fuelwood. A typical household
of eight people
who use
fuelwood for cooking on a traditional stove (thermal efficiency of
17%) at a
rate of 300 watts/person will consume about 150 GJ of energy in
a two-year
period. Alternatively, if this same
household did their
cooking on two
$3 improved channel-type woodstoves, which have observed
fuel savings
of 30-40% in the field (thermal efficiency of 30%, Chapter
V), they
would only consume 90-105 GJ over the two-year life of these
stoves.
The energy savings would be achieved at a
cost of just $0.10-0.13/GJ
-- a factor
of 10 less than the cost of plantation produced
fuelwood
(Table 19). The energy needed to
produce these stoves does not
change this
result. Currently, 0.022-0.027 GJ/kg is
needed to produce
steel from
raw ore and new industrial processes could reduce this to
0.009-0.012
GJ/kg (136). A typical stove might use
2-3 kg of steel and
thus require
0.1 GJ to produce while saving 25 GJ or more over its
lifetime.
Comparing
these options in this manner is not intended to argue that
improved
stoves are a substitute for planting trees.
Both are needed now
and both are
important components of any longer-term energy strategy.
The cost of
providing such fuel efficient stoves to every family on earth
now using
biomass fuels for cooking would be less than a typical 1 GW
nuclear power
plant, yet save some 10-20 times as much energy each year as
the reactor
would produce during its entire lifetime (153).
The design,
production,
and dissemination of low-cost, fuel efficient biomass stoves
and other
technologies are the subjects of the following chapters.
CHAPTER III
STOVE DESIGN
In this
chapter the basic physical principles of combustion and heat
transfer will
be applied to the design of cookstoves burning raw biomass
fuels such as
wood and agricultural wastes and guidelines for improving
their
efficiency will be developed. These
guidelines form the basis for
the
development of highly fuel efficient stoves.
These are, however,
guidelines
only. To determine accurately the
effects on performance of
various
design modifications and to optimize a design requires painstaking
testing as
described in Chapter V. The actual
combustion and heat transfer
processes
occurring in a stove are too complicated, too highly interdependent,
and too
variable to model and predict easily.
Testing is a must.
To begin
understanding how to improve the performance of a stove, both the
theoretical
limits as well as the current practical limits to stove
performance
must be understood. The theoretical limits
are examined first.
Consider, for
example, cooking rice or porridge. As
shown in Table 1,
heating the
appropriate amounts of dry grain and water to boiling and
inducing the
necessary chemical reactions requires, in this ideal case,
the
equivalent of about 18 grams of wood per kilogram of cooked food.
Yet,
controlled
cooking tests with the open fire have required some 268 grams
of wood per
kilogram of food cooked and even improved metal stoves have
used some 160
grams -- nine times the theoretical requirement.
(Chapter V
and reference
2).
To determine
where the rest of this energy is lost requires detailed
experimental
work, including monitoring stove wall temperatures, flue gas
temperatures
and volumes, and emissions, and has only been done in a few
bse1x290.gif (600x600)

special cases
(3-5). Some of these are sketched in
Figure 1 below.
TABLE 1
Energy Required For
Cooking
Specific
Temperature
Energy Required Total
Wood Equivalent
Heat
for Chemical
Cooking
(grams)
Food
kJ/kg[degrees]C
Change [degrees]C
Reactions Energy
per kg Food
kJ/kg
kJ/kg
Cooked
Rice
1.76-1.84
80
172 330(*)
18
Flour
1.80-1.88
80
172 330(*)
18
Lentils
1.84
80
172
330(*)
18
Meat
2.01-3.89
80
-- 160-310
9-17
Potatoes
3.51
80
-- 280
16
Vegetables
3.89
80
--
310
17
(*) This
includes sufficient water for cooking but none for evaporation
(**) For wood
with a calorific value of 18 MJ/kg.
References
(1,3).
From these
heat balances, several observations can be made.
o Generally the largest loss, 14-42% of the
input energy, is by beat
conduction into and through the
walls. In massive stoves
bse1c290.gif (486x486)

bse1bx29.gif (486x486)

stove (Figure lb) it is conducted through
and lost from the outside
bse1a.gif (388x432)

surface.
o The loss of energy in hot flue gas
accounts for some 22-39% of the
total input to the woodstove.
The energy efficiency of a stove can be
dramatically increased by making use of
the energy in this hot flue gas
through improved convective heat transfer
to the pot.
o Although not explicitly detailed in Figure
1a, in open fires radiant
bse1a.gif (353x437)

heat transfer is the mechanism for
two-thirds of the heat transfer to
the pot and cannot be greatly increased
(7).
o The energy losses due to incomplete
combustion are relatively small,
typically less than 8% of the input
energy. The greater problem with
incomplete combustion is the emission of
poisonous carbon monoxide and
hydrocarbons -- many of which are toxic,
even carcinogenic (8).
o Typically half the energy entering the pot
is lost in the form of steam
bse1a290.gif (281x432)

losses also occur in getting that energy
into the pot. Eliminating this
steam loss by more carefully controlling
the fire could, in principle,
reduce total energy use by half.
Similarly, convective heat losses from
the surface of the pot are quite important
(Figure 1d). For typical pot
bse1dx30.gif (437x486)

loss rates of 700 W/[m.sup.2] (42,43), a
28-cm-diameter cylindrical pot with
10-cm exposed to ambient air will lose
energy at the rate of 100 W.
Over an hour, this is energetically
equivalent to 20 grams of wood.
FIGURE 1:
Heat Balances In Cooking Stoves
Figure 1a:
Traditional Open Fire
Final Energy
Balance:
Gains:
8% absorbed
by water and food
Losses:
10% lost by
evaporation from pot
82% lost to
environment
Reference (6)
Figure 1b:
Two pot uninsulated metal
wood stove
with chimney.
Final Energy
Balance:
Gains:
17.6%
absorbed by first pot
10.3%
absorbed by second pot
the fraction lost by evaporation
from pots is unknown
Losses:
2% absorbed by stove body
40.4% lost by
convection and radiation
from stove body
22.2% lost as
thermal energy in
flue gases
7.8% lost due to incomplete combustion
Reference (5)
Figure 1c:
Two pot massive wood
stove with
chimney.
Final Energy
Balance:
Gains:
11.8%
absorbed by first pot
3.6% absorbed by second pot
Losses:
29.2%
absorbed by stove body
1.9% lost by convection and radiation
from stove body
39.0% lost as
thermal energy in
flue gases
2.7% lost due to incomplete combustion
11.8%
unaccounted for
Reference (5)
Figure 1d:
Three pot mass wood
stove with
chimney.
Final Energy
Balance:
Gains:
6% absorbed by water and food
Losses:
4% lost by evaporation from pots
2.1% lost from pot surfaces
13.9%
absorbed by stove body
30.2% lost as
thermal energy in
flue gases
1.1% lost as carbon monoxide
1.9% lost to evaporate moisture in
fuel
5.9% lost as latent heat of vaporization
of water produced
by combustion
11.% lost as charcoal residue
Reference (3)
Figure 1e:
Thai charcoal stove.
Final Energy
Balance:
Gains:
3.1% absorbed by water and food
Losses:
4.6% lost by evaporation from pot
0.2% lost by convection and
radiation from pot lid
13.0%
absorbed by stove body
1.3% lost by convection and radiation
from stove body
2.1% lost as thermal energy in
flue gases
0.7% lost as carbon monoxide due
to incomplete combustion
75.% lost in the conversion of
wood to charcoal
Reference (4)
Improving the
fuel efficiency of a stove thus requires attention to a
number of
different factors. Among these are:
Combustion Efficiency: so that as much of
the energy stored in the combustible
as possible is released as heat.
Heat Transfer Efficiency: so that as much
of the heat generated as
possible is actually transferred to the
contents of the pot. This
includes conductive, convective, and
radiative heat transfer processes.
Control Efficiency: so that only as much
heat as is needed to cook the
food is generated.
Pot Efficiency: so that as much of the
heat that reaches the contents
of the pot as possible remains there to
cook the food.
Cooking Process Efficiency: so that as
little energy as possible is
used to cause the physico-chemical changes
ocurring in cooking food.
The
combustion and heat transfer efficiencies are often combined for
convenience
and are then termed the thermal efficiency of the stove.
When
they are also
combined with the control efficiency, the three together are
termed the
stove efficiency. Different tests
measure different combinations
of these
factors. High power water boiling
tests, for example,
measure the
thermal efficiency. High/low power
water boiling tests and
controlled
cooking tests are two different methods of measuring the stove
efficiency.
The heat
transfer efficiency will be discussed first in terms of the
conductive,
convective, and radiative processes going on in and around the
stove.
These processes are sketched in Figure
2. The other aspects of
bse2x32.gif (600x600)

efficiency
will be discussed in turn. The
appendixes document the text in
detail and
provide extensive references for further reading.
CONDUCTION
The
temperature of a solid, liquid, or gas is a measure of how rapidly the
atoms and
molecules within it are moving: the
faster they are moving the
hotter the
substance is. In gases and liquids,
conductive heat transfer
occurs when
high velocity molecules randomly collide with slower molecules,
giving up
some of their energy. In this way, heat
is gradually
transferred
from higher temperature regions to those at lower temperatures.
Because of
their low density and the consequent low collision rate
between
molecules, gases have a low thermal conductivity.
High quality
insulators
take advantage of this by trapping millions of miniscule air
pockets in a
matrix of (very porous or spongy) material: most of such
insulators is
in fact air. The solid material is
there only to hold the
air in place
-- to prevent currents of air that would increase the heat
transfer
rate. Thus, such insulators lose some
of their insulating value
if they are
compressed, which reduces the size of the air pockets, or get
wet, which
fills the air pockets with higher conductivity water.
TABLE 2
Typical Property Values at
20[degrees]C
Material
Thermal
Density
Specific Heat
Conductivity
kg/[m.sup.3]
J/kg[degrees]C
Metals
W/m[degrees]C(*)
Steel Alloys
35 (10-70)
7700-8000 450-480
Nonmetallic
solids
Cement
0.8-1.4
1900-2300 880
Insulators
Fiberglass
0.04
200 670
Liquids
Water
0.597
1000
4180
Gases
Air
0.026
1.177
1000
(*) See
Appendix I for the definition and conversion of units.
Reference
(9). A more complete table is given in Appendix A.
In a solid,
heat is conducted as more rapidly vibrating atoms excite and
speed up the
vibration rate of more slowly moving neighbors.
Additionally,
in metals
heat is conducted as free electrons with a high velocity move
from regions
at a high temperature into regions at a lower temperature
where they
collide with and excite atoms. In
general, heat conduction by
such
electrons is much more effective than that by adjacent atoms exciting
each
other. For this reason, metals (which
conduct electricity) have much
higher
thermal conductivities than electrically insulating solids.
A brief table
of thermal conductivities and other factors is presented in
Table 2
above. The points just made about the
low conductivity of gases,
the high
conductivity of metals, and quality insulators being mostly air
(notice the low
density) can be clearly seen in this table.
Calculating
Thermal Conductivity
bse3x33.gif (317x317)

The thermal
conductivity of an object can
be expressed
approximately by the equation
kA([T.sub.1] - [T.sub.2])
Q= ---------------------------
(1)
s
where Q is
the rate of heat transfer, k is
the thermal
conductivity of the material,
A is the
area, s is the thickness of the
object across
which heat is being conducted,
and
([T.sub.1-[T.sub.2]) is the temperature difference
between the
hot and cold sides. Thus, we see that
if the plate is
large and
thin (A/s large) the rate of heat tranfer will be large. If the
plate is
small in area and thick, more like a rod (A/s small), the rate of
heat transfer
will be small. The heat transfer also varies
directly with
the thermal
conductivity and the temperature difference across the object
(Appendix A).
However,
using this equation alone for the heat transfer across a stove
wall would
lead to values that are many times too large.
The heat transfer
into and out
of an object depends on the conductivities to and from the
surfaces as
well as the conductivity within the object itself (Appendix
A).
In some cases, dirt or oxide layers may
reduce the heat transfer
across the
surface; in other cases, the air at the surface itself significantly
reduces the
heat transfer. Taking this into account
then gives
A([T.sub.1] - [T.sub.2])
Q = ------------------------
1
s 1
-
+ -
+
-
[h.sub.1]
k [h.sub.2]
(2)
where
[h.sub.1] and [h.sub.2] are the inner and outer surface heat transfer
coefficients
(Appendix
B). Typical values for h are 5
W/[m.sup.2][degrees]C in still air to over 15
W/[m.sup.2][degrees]C
in a moderate 3 m/s wind. The inverse
values 1/h and s/k are the
thermal
resistances to heat transfer. Typical
values of the thermal
resistances
(s/k) for different stove walls are 0.0000286 [m.sup.2][degrees]C/W for
1-mm-thick
steel, 0.04
[m.sup.2][degrees]C/W for 2-cm-thick fired clay, and 0.10 [m.sup.2][degrees]C/W
for a
10-cm-thick
concrete wall. In contrast, the thermal
resistance of the air
at the
surface of the stove wall (1/h) is 0.2 [m.sup.2][degrees]C/W for still air and
0.0667 [m.sup.2][degrees]C/W
for a 3 m/s wind. These values must
then be doubled to
account for
both the inside and outside surfaces.
Thus, it is
the surface resistance, not the resistance to heat transfer of
the material
itself, that primarily determines the rate of heat loss
through the
stove wall. This is true until very low
conductivity (high
thermal
resistance) materials such as fiberglass insulation are used.
Fiberglass,
for example, has a thermal resistance (1/k) typically about 25
m[degrees]C/W
or, for a 4-cm-thick lining, a total resistance (s/k) of about I
[m.sup.2][degrees]C/W.
In this case the insulation, not the
resistance of the surface
air layers,
is the primary determinant of the stove's rate of heat loss.
The steady
state rate of heat loss through a metal stove wall can now be
crudely
estimated. If the wall has an area of
1mx0.2m-0.2[m.sup.2], a temperature
difference of
500[degrees]C between the inside and outside, and is in still air
(.2)(500)
Q= ------------------------
= 250 watts
(.2) + (0.0000286) + (.2)
If the
resistance of the surface boundary layer of air had been ignored, a
rate of heat
loss 14,000 times greater would have been calculated -- an
absurdly
large value.
Conductive
heat transfer also carries heat through the pot to its contents.
High
conductivity aluminum pots can save energy compared to clay
pots because
they more readily conduct the heat of the fire to the food.
At the same
time, however, aluminum pots will suffer greater heat loss
than clay
pots from the warm interior to the portions of the exterior exposed
to cold
ambient air. These portions of the pot
could be insulated to
reduce this
heat loss. The overall heat transfer
coefficient of aluminum
pots has been
estimated to be about 18 W/[m.sup.2][degrees]C compared to 9.7
W/[m.sup.2][degrees]C for
clay pots
(3,10). In controlled cooking tests
with aluminum pots, fuel
savings were
about 45% (3) compared to using clay pots.
Coating aluminum
pots with mud
to protect their shine, or allowing a thick layer of soot to
build up on
the outside reduce the pots' energy efficiency and should be
discouraged.
In addition to their high performance and
ease of use cooks
prefer
aluminum pots because, unlike traditional fired clay pots, they
won't
break. In a very few years the
production and use of aluminum pots
has spread
widely in many developing countries.
Calculating
Thermal Storage
Another
factor of importance in conductive heat transfer calculations is
the ability
of a material to store thermal energy, measured as its
specific
heat. The specific heat of a material
is the amount of energy
required to
raise the temperature of 1 kg of its mass by 1[degrees]C.
For a given
object, the
change in the total heat stored is then given by
dE - [MC.sub.p](dT)
(3)
where M is
the object's mass, [C.sub.p] is its specific heat, and (dT) is its
change in
temperature. Thus, if the wall of a 3
kg metal stove increases
by
380[degrees]C during use, the change in energy stored in its wall is
dE =
(3kg)(480Ws/kg[degrees]C)(380[degrees]C) = 547200 Ws or 547.2 kJ
Thus, the
thermal conductivity carries thermal energy through a material;
the specific
heat and mass of an object store this heat energy.
The
larger the
mass and specific heat of an object the more energy it can
store for a
given change in temperature. Thus a
thermally massive (large
[MC.sub.p])
object warms up slowly; a thermally lightweight (small [MC.sub.p]) object
will warm rapidly.
This is called the thermal inertia of an
object and is
an important
design parameter in stoves.
Wall Loss
Calculations
Reducing the
heat loss into and through the stove walls to the outside
requires a
detailed analysis of the conduction process, which is presented
in Appendix
A. In reviewing these calculations, it
is important to note
first that
they are based on a particular assumed combustion chamber
geometry and
heat flux from the fire. Because of
this, the values listed
below are in
watts, degrees, etc., rather than in dimensionless units.
Second, for
simplicity and convenience the calculations were done assuming
that the fire
is kept at a single power level all the time.
Thus, the
results
listed are intermediate between those observed in practice for the
high power
boiling phase and the low power simmering phase due to the
assumed
values for the heat fluxes. Although
the values given are shifted
by these
factors, they nevertheless show trends that will remain the same
for any
combustion chamber.
When cooking
begins, the walls of the stove are cold.
With time they warm
up at a rate
determined by their mass and specific heat as discussed
above.
Lightweight walls have a low thermal inertia
and warm quickly.
Thick, heavy
walls warm more slowly. Heat loss from
the combustion chamber
is determined
by how quickly these walls warm and subsequently how much
heat the wall
loses from its outside surface. This is
shown clearly in
bse4x37.gif (600x600)

Figure 4,
where the thicker the wall the more slowly it warms.
Although a
thick wall of dense high specific heat material may have
slightly
lower heat loss than a thinner wall after several hours (See
Appendix A),
it takes many hours more for the eventual lower heat loss of
the thick
wall to compensate for its much greater absorption of heat to
warm up to
this state. Thus, it is always
preferable to make the solid
(non-insulator)
portion of the wall as thin and light as possible.
Additionally,
the use of lightweight insulants such as fiberglass or
bse4bx37.gif (486x486)

double wall
construction can dramatically lower heat loss (Figure 4B).
Materials
such as sand-clay or concrete, which have a high specific heat
and density,
and which must be formed in thick sections to be sufficiently
strong to
support a pot or resist the fire, should therefore be avoided.
Heat
Recuperation
It has
frequently been argued that the large amounts of heat absorbed by
the walls of
a massive stove should be utilized by either extinguishing
the fire
early and using this heat to complete cooking or by later using
it to heat
water. Water heating tests on hot
massive stoves, however, have
shown that
only 0.6-1.3% of the energy released by the fire, of which
perhaps
one-third was stored in the massive wall, could be recuperated -- heating
the water by
typically 18-19[degrees]C (2). What is
often thought to be
heating or
cooking by heat recuperation is actually done by the remaining
coals of the
fire.
That heat
recuperation from massive walls is so difficult can be easily
understood by
considering the following. First, heat
conduction through
the wall is
slow (Appendix A) so that little energy can be transported to
the pot
directly. Second, air is a relatively
good insulator. Thus, little
heat can be
carried from the wall into the air space inside the stove and
then to the
pot. Third, both of these heat paths
are further slowed by the
relatively
small temperature difference between the wall and the pot.
The
low
temperature of the wall also reduces the radiant transfer to the pot.
Finally, the
heat stored in the wall tends to equilibrate within the wall
and then leak
to the outside. The result of all these
processes is shown
bse6x39.gif (600x600)

in Figure 6
and agrees very well with the experimental data cited above.
Rather than
depending on low efficiency massive stoves (Table V-1) for
cooking and
then attempting to recuperate heat for hot water, such water
heating can
be much more efficiently done directly with a high performance
stove.
Further, it can then be done when needed
rather than being tied to
the cooking
schedule. Similarly, using stored heat
to complete cooking is
an extremely
inefficient technique compared to using a high efficiency
lightweight
stove and possibly a "haybox" cooker (discussed below under
OTHER
ASPECTS).
Heat
recuperation is clearly desirable, however, when it can be done
efficiently,
cost effectively, and without excessively interfering with
the primary
purpose of the device. For example,
heating water by heat
recuperation
might be efficiently done by forming the wall of a high
performance
metal stove itself into a water tank.
Heat that would otherwise
be lost into
and through the wall would then instead be directly
absorbed by
the water. Whether
or not the lower average combustion
chamber
temperatures would significantly reduce the pot heating efficiency
or interfere
with combustion would need to be tested.
Thus,
lightweight walls have the intrinsic potential for much higher
performance
than massive walls due to their lower thermal inertia.
This
does not,
however, necessarily mean that a lightweight stove will automatically
save energy
or that a massive stove cannot. For a
lightweight
stove to save
energy its heat loss to the exterior must also be minimized
and the
convective and radiant heat transfer to its pot must be optimized.
Conversely, massive
stoves can and sometimes do save energy despite their
large wall
losses. Such stoves can save energy if
the convective and
radiative
heat transfer to the pot is carefully optimized.
Reducing Wall
Losses
If a
lightweight single wall (metal) stove is heavily tarnished and sooted
bse5x39.gif (600x600)

on the
outside its exterior heat loss can be quite large (Figure 5).
This
heat loss is
due to the emission of radiant energy (see Appendix C) and
can be
reduced by chemically or mechanically polishing or coating the
exterior
surface to leave a bright metallic finish.
Although such a finish
may have
commercial appeal, its effectiveness in reducing heat loss will
last only so
long as it is kept relatively clean and free of soot and
rust,
etc. It should be noted that most paints,
even white paint, will
actually
increase the radiant heat loss from a stove and should be
avoided; to
decrease radiant heat loss, the surface must be metallic.
Lighweight
single wall stoves are easy to construct, are low cost, and
have
relatively high performance when convective heat transfer is optimized.
However,
during use they can be quite hot on the outside and can
bsex40.gif (600x600)

burn the user
as well as be uncomfortable to use (Table 3).
To reduce heat
loss and thus
reduce this hazard, either double wall construction and/or
lightweight
insulants such as fiberglass or vermiculite can be used.
Double wall
construction with metal alone can significantly reduce heat
loss (Figure
5), user discomfort, and the hazard of burns (Table 3).
The
double wall
serves two functions in reducing heat loss.
First, the dead
air space
between the two walls is a moderately good insulator.
It should
be noted,
however, that increasing the thickness of this dead air space
does not
improve its insulating value. This is
due to the convection
currents,
which flow more freely the larger the space, carrying heat from
one wall to
the other. Second, the inner wall acts
as a radiation shield
between the
fire and the outer wall. Both of these
factors can be seen in
Figure 5.
There, the emissivity or, more accurately, the radiant coupling
between the
inner and outer walls is the prime determinant of heat loss.
The exterior
surface emissivity is less important due to the lower temperature
of that
wall. As the temperature of the exterior
wall increases due
to greater
radiant heat transfer from inner to outer wall ([[epsilon].sub.i] increasing)
the exterior
emissivity, [[epsilon].sub.e], becomes more important (Appendix C).
In practice
there are several potential difficulties:
o
Although it is preferable to minimize
radiant coupling between the two
walls by giving them a bright, long-lasting
metallic finish, they will
tend to rust, tarnish, and soot over
time. Keeping them clean would be
difficult.
Even in the worst case ([[epsilon].sub.1] = .9, [[epsilon].sub.e] .9),
however, the double
wall still performs better than the best
([epsilon].sub.e] = .9) single metal wall.
o
The dead air space is a good insulator on
its own, but attaching the
inner wall to the outer will tend to short
circuit its insulating value
due to the high thermal conductivity of
metal. It is necessary that the
two walls together be mechanically rigid,
but they should not easily
conduct heat from one to the other.
This might be done by using nonmetallic
spacers or fasteners, or tack welding the
walls together at
selected points.
Long continuous welds should be avoided if possible.
o
The insulating value of the dead air space
is reduced if air is allowed
to flow through.
Thus, the dead air space should be closed at the top.
Double wall
metal stoves are now being developed and commercialized in
Botswana
(11,12) and Guinea (13).
Better yet is
to use a high quality insulant such as fiberglass or
vermiculite
with the double wall to hold it in place and protect it.
As
seen in
Figure 5, layers of insulation as thin as a few millimeters are
effective in
reducing heat loss. Such stoves have
been tested in Mali
(14).
Other lightweight insulants worth
investigating include wood ash,
diatomaceous
earth, and, possibly, chemically treated (to reduce its
flammability)
straw or charcoal among others (see Table A-1).
Just as
insulated walls reduce the exterior temperatures (Table 3), they
increase the
inner wall temperature. This can
increase heat transfer to
the pot by
convective heat transfer, by radiative heat transfer from the
inner wall
surface, and possibly by improving the quality of combustion.
CONVECTION
Convective
heat transfer occurs when a gas or liquid is forced or flows
naturally
into a region at a different temperature and then exchanges heat
energy by
conduction - - by the interaction of individual particles.
It is
by convective
heat transfer that the hot gas leaving the fire heats the
pot, or that
the wind cools a hot stove. In open
fires and many traditional
bse1x290.gif (600x600)

stoves much
of the heating potential of this gas is lost (Figure 1).
Increasing
convective heat transfer to the pot is the single most
important way
to increase the thermal efficiency of a woodburning stove.
Increasing
Convective Heat Transfer
In general,
convective heat transfer is given empirically by the equation:
Q = hA([T.sub.1]-[T.sub.2])
(4)
For the case
of a pot being heated by hot gas leaving the fire, Q is the
heat
transferred from the gas to the pot, h is the convective heat
transfer
coefficient, A is the area of the pot across which the heat
exchange
takes place, and ([T.sub.1]-[T.sub.2]) is the temperature difference between
the hot gas
and the pot.
To increase
the heat transfer Q to the pot there are then, in principle,
three things
one can do. First, the temperature
[T.sub.1] of the hot gas can be
increased.
This can be done only by closing the stove
and controlling the
amount of
outside air that enters. This is often
impractical as it
requires
manipulating a door on the wood entry, prevents easy visual monitoring
of fire, and
usually requires cutting the wood into small pieces so
that the door
can be closed behind them. Further, the
user must consistently
close the
door. Stoves with enclosed fireboxes
are, however, being
developed and
disseminated in India (15-18). If
successful on a large
scale, this
is an important innovation.
Second, as
much of the area A of the pot should be exposed to the hot gas
as
possible. This is very important.
The pot supports, for example, must
be strong
enough to support the pot but should be kept small in area so as
not to screen
the hot gas from the pot. The gas
should be allowed to rise
up around the
pot and contact its entire surface.
Third, the
convective heat transfer coefficient h should be increased.
This can be
done by increasing the velocity of the hot gas as it flows
past the pot.
In convective
heat transfer, the primary resistance to heat flow is not
within the
solid object (unless it is a very good insulator), nor within
the flowing
hot gas. Instead, the primary
resistance is in the "surface
boundary
layer" of very slowly moving gas immediately adjacent to a wall.
Far from a
wall, gas flows freely and readily carries heat with it.
As the
pot wall is
approached, friction between the pot and the gas prevents the
gas from
flowing easily, Within this region, heat transfer is primarily by
conduction
and, as previously noted, the conductivity of gases is quite
low.
It is this surface boundary layer of
stagnant gas that primarily
limits heat
transfer from the flowing hot gas to the pot.
To improve
the thermal efficiency of a stove, the thermal resistance of
this boundary
layer must be reduced. This can be
accomplished by (among
others)
increasing the flow velocity of the hot gas over the surface of
the pot.
This rapid flow helps "peel" away
some of this surface boundary
layer and,
thinner, the boundary layer of stagnant gas then offers less
bse7x43.gif (600x600)
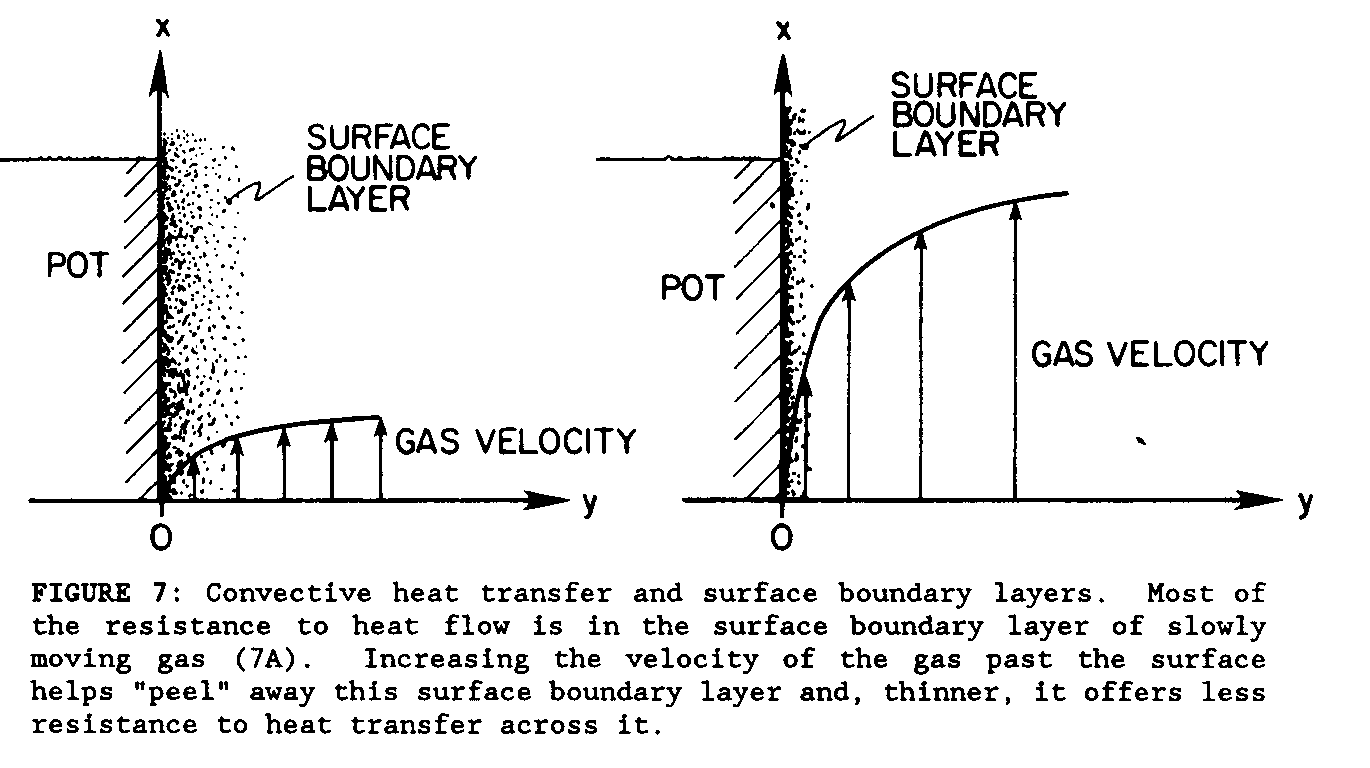
resistance to
conductive heat transfer across it to the pot (Figure 7).
Fundamental
Stove Types
Efforts to
improve convective heat transfer have resulted in three
fundamental
types of biomass stoves, which will be generically termed
multipot,
channel, and nozzle (Figure 8). In each
of these, the flow
bse8x44.gif (600x600)

velocity of
the hot gas over the pot is increased by narrowing the
channel(1)
gap through which the gas must flow past the pot.
(Because the
volume of hot
gas flowing past any point is constant, its flow velocity
through a
narrow gap must be faster than through a wider one).
This,
however,
results in a serious handicap inherent in any improved stove
program.
As these channel gaps must be precise to
within a few millimeters
to be
effective, stove and pot dimensions must correspond and be precisely
determined -
- greatly complicating both production and dissemination.
Multipot
stoves heat two or more pots from a single fire.
In principle,
this
increases the pot surface area exposed to the fire and hot gas and
raises the
thermal efficiency. In practice,
however, it is difficult if
not
impossible to individually control the heat input to each of the pots
(see OTHER
ASPECTS). The resulting stove
efficiency is then usually lower
than channel
or prototype nozzle stoves now under development.
Channel
stoves increase the pot area exposed to the hot gas by forcing the
gas over as
much of the surface of a single pot as practicable.
Radiant
transfer is
maximized by placing the pot close to the firebed yet without
excessively
interfering with the combustion.
Channel stoves offer higher
______________________
(1) The channel dimensions are called
"length" for the direction of gas
flow,
"width" for the circumference of the pot or stove, and
"gap" for the
space between
the pot and stove walls.
efficiencies,
better control, and lower cost than most multipot stoves.
Emissions
from channel stoves, however, are often no less than from
multipot
stoves and in some cases may be worse.
The
development of nozzle type stoves has only recently begun (18,19), yet
they appear
to offer considerable promise. As for
channel stoves, nozzle
stoves have a
single pot, the entire surface of which is exposed to the
f ire and hot
gas. Similarly, as for both channel and
multipot stoves,
nozzle stoves
increase the velocity of the hot gases flowing past the pot
by forcing
them through a narrow channel.
Additionally, the large height
and the
narrowing throat of the nozzle stove's combustion chamber accelerate
the gases to
a higher velocity before they contact the pot.
This is
done,
however, at the expense of reduced radiant transfer.
Prototype
nozzle stoves have achieved efficiencies of 43% in laboratory
tests
(18,19), comparable to the best multipot stoves (15-17) and channel
stoves
(14). Further, because the shape of the
combustion chamber improves
combustion,
nozzle stoves have much lower emissions than other types.
Recent tests
of nozzle stoves have shown emissions of carbon monoxide (CO)
to be just
5-6 ppm at peak power and of soot, less than 2.5 mg/[m.sup.3] (18,19).
These are far
less than the open fire. By comparison,
typical emissions
from kerosene
stoves at peak power are 25 ppm of CO and 0.2 mg/[m.sup.3] of soot.
Current
prototypes, however, suffer the severe handicap of accepting only
very small
pieces of biomass. Whether or not this
can be overcome remains
to be
seen(2).
______________________
(2) For further information, readers
should contact H.S. Mukunda and U.
Shrinivasa at
ASTRA (See Appendix J).
Modeling Convective
Heat Transfer
Understanding
convective heat transfer underpins all efforts to improve
the
efficiency of biomass burning stoves. A
detailed empirical model of
convective
heat transfer in channel stoves is developed in Appendix B;
references to
an empirical model of multipot stoves are also provided
there.
Numerical analysis of convective heat
transfer in channel and
nozzle stoves
is now underway by the author and will be presented elsewhere.
Because
channel stoves generally have much better performance than
multipot
stoves and because they are more fully developed and tested than
nozzle
stoves, critical elements in their design will be presented here.
The empirical
model of convective heat transfer in channel stoves developed
in Appendix B
provides considerable insight into their performance
and
limitations. This model is not
sufficiently precise to be used to
predict the
absolute quantitative performance of a real stove -- that can
only be done
by detailed testing as discussed in Chapter V.
Nevertheless,
the model is
useful in illustrating general trends in the performance of
this type of
stove and its sensitivity to dimensional changes.
From the
above discussion of convective heat transfer and surface boundary
layers one
expects narrower channels to have higher rates of heat transfer
to the
walls. This is clearly seen in the
model predictions presented in
Figure
9. In fact, the channel efficiency,
defined as the fraction of
energy in the
hot gas entering the channel that is transferred to the pot,
is extremely
sensitive to changes in the channel gap.
For a 10-cm-long
channel, the
channel efficiency drops from 46% for an 8-mm gap to 26% for
a 10-mm
gap. Thus the stove and pot dimensions
must be very precisely
controlled.
Multipot and nozzle stove performance is
similarly sensitive
to the
channel gap.
The lower
efficiency of wide channel gaps can be partially compensated for
bse9x46.gif (600x600)

by making the
channel longer (Figure 9) or by closing the combustion
chamber to
control excess air and thus raising the average gas temperatures
(Appendix
B). However, closing the firebox is
often not practical,
as discussed
below under Radiation, and longer channels can seldom fully
bse9bx46.gif (486x486)

compensate
(Figures 9,11). As seen in Figure 9B,
additional channel length
bse9x460.gif (600x600)

is also less
and less effective. As the gases in the
channel rise and
give up their
heat, their temperature drops.
Additional channel length is
trying to
recuperate energy from this increasingly lower temperature
(lower
quality) heat source. For the 4-mm gap,
effectively all the energy
in the gas
that can be is recuperated in the first 2 cm length of the
channel.
Channels longer than 5 cm are useless.
For the 6-mm gap, the
first 5 cm
length recuperates 57% of the energy in the gas, the next 5 cm
recuperate an
additional 16%, the next 5 cm an additional 8%, and so on.
Whether the
additional length is worthwhile depends on local fuelwood
prices, the
construction costs for longer channels, and other factors.
This can only
be determined by careful testing of the stove to determine
the actual
performance tradeoffs of channel width and length and the
resulting
financial benefits.
Although
narrow channels have high efficiencies, they also reduce the
amount of gas
that can flow through the channel and thus limit the
bse10x47.gif (534x534)

firepower
(Figure 10). With a too narrow channel
or a too large fire
either the
smoke will pour out the stove door, or else the fire will be
choked and
suffer poor combustion or simply not build up to the desired
power.
In either case, stove efficiency suffers.
Additionally, with a
too narrow
channel, there will be such a small fire that the pot cannot be
heated in a
reasonable length of time. Thus, the
choice of optimum
channel width
is a compromise between high efficiency and rapid heating.
bse11x48.gif (600x600)

Figure 11 illustrates
this compromise.
To translate
the above results into a total stove efficiency, it will be
assumed here
that the efficiency for the pot alone (due to radiation and
convection on
its bottom) is 20% and that a third of the total firepower
is available
in the hot gases entering the channel.
The total stove
efficiency is
then 20% plus one-third of the channel efficiency.
With these
assumptions the total stove efficiency can be graphed versus
the total
heat flux to the pot (Figure 11). Now
the tradeoffs between
channel gap
and length and between stove efficiency and heating rate can
be clearly
seen. For example a stove (0.3-m
diameter) with about a 40%
total
efficiency could have a channel gap of 6 mm and length of 5 cm or
one of 8 mm
by 20 cm. However, the 6-mm stove would
have a peak heat flux
to the pot of
1.3 kW while the 8-mm stove would provide nearly 3 kW.
In
fact, for
reasonable channel lengths, the 6-mm channel could never reach 2
kW.
Similarly, if a stove capable of providing 4
kW to the pot was needed,
a channel gap
of about 9-10 mm would be necessary (4 kW will raise 10
liters of
water to boiling in about 14 minutes).
Thus, higher total stove
efficiencies
can be achieved but must be balanced with the heating rate
and possibly
the cost of constructing a long channel.
It should be
remembered,
however, that all of these efficiencies and resulting heating
rates are
higher than those of the protected open fire.
To this
point, the hypothetical stove model has been operated at its
optimum power
level. At powers greater than the
optimum the combustion
gases cannot
all escape out the channel and instead must flow out the door
or perhaps
suffocate the fire and lower the combustion quality.
At powers
below the
optimum, the gas flow through the channel will remain about the
same but will
be at a lower temperature due to more entrained air (less
gas at a
higher temperature will accelerate due to its larger buoyancy and
pull in cold
air until it reaches a new, lower temperature equilibrium
flow
rate). In either case, the efficiency
drops. Experimental work has
shown that
for a variety of stoves the efficiency has a maximum at a
particular
fire power (5).
From Figure
11, it can be seen that to allow rapid initial heating, a
larger
channel gap may be needed: during simmering, the stove efficiency
then
suffers. Alternatively, if a slightly
narrower channel gap is chosen,
the higher
efficiency during the simmering phase will be at the expense of
slower
initial heating. A variable channel gap
would be desirable, but is
difficult to
realize in practice. Depending on how
sensitive the stove
efficiency is
to the power level, a compromise between rapid heating and
efficient
simmering may be necessary. This choice
must be determined in
part by the types
of food to be cooked. If cooking times
are short,
heating
should be emphasized; if long, simmering efficiency may be more
important.
Fortunately, these tradeoffs are not usually
very severe.
For any
estimated heat flux from Figure 11, the time required for the pot
to come to a
boil is given by
t =
4.186x[10.sup.3]V[delta(difference)]T
------------------------------------- minutes
60P
where V is
the volume of water in the pot in [m.sup.3], [delta(difference)]T is the
temperature
change in the
water to reach boiling, and P is the heat flux to the pot in
kW from
Figure 11. Additionally, the heat loss
of approximately 0.7 kW/[m.sup.3]
from the lid
(at T-100[degrees]C) should be subtracted from P (39) but is ignored
here.
Thus, for an industrial stove with G=14mm,
L=0.5m, V=0.5 [m.sup.3] and
[delta]T=80[degrees]C,
the time to reach boiling is t=71 minutes.
Finally, it
is important to note that insulating the walls assists
bse12x50.gif (600x600)
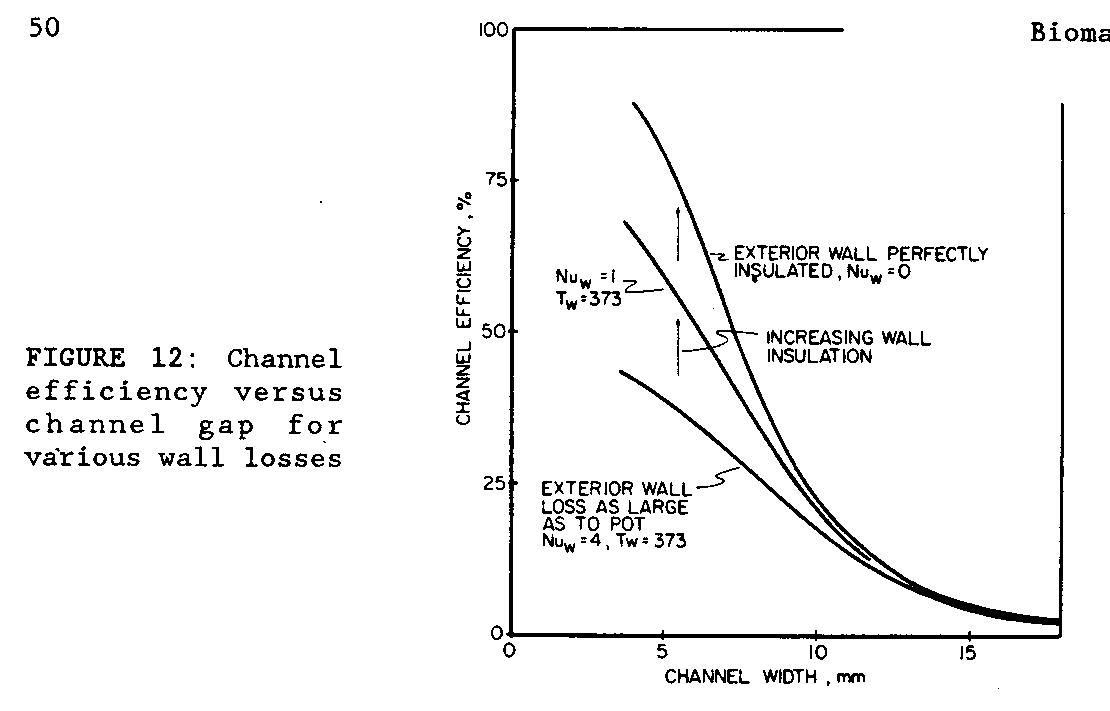
convective
heat transfer (Figure 12). For stoves
with dimensions optimized
for
convective heat transfer, this can be a significant potential.
The necessary
precision of a few millimeter in the channel gap dimensions
found above
has some very important consequences.
Such high precision in
stove and pot
dimensions requires centralized artisanal or industrial mass
production
based on standardized templates and molds.
Owner-built or
site-built
stoves can rarely be made so precisely.
In those few cases
where they
are, it is all but impossible to replicate the feat on a large
scale
involving many thousands of stoves and stove builders in widely
separated
locations. Such precision also implies
that stoves should not
be made of
sand-clay, concrete, or other materials in which dimensional
control is
difficult. For these materials, walls
of sufficient strength
to support
the pot are also so thick that they shield much of the pot from
the hot gas
-- reducing convective heat transfer.
Many design
variations are possible that will help reduce these problems.
bse8x44.gif (600x600)

Vertical
walls, as shown for the channel stoves in Figure 8 and the inset
diagrams of
Figures 9 and 11, strictly limit the acceptable pot size to
within a few
millimeter of the optimum. Nor can this
limitation be avoided
if the stove
and pot walls have the same shape. In
many cases, however, a
spherical pot
will be used with a straight-sided stove wall (Chapter IV--Template
Design:
Cylindrical Stoves). In this case, if
the walls where the
pot sits are
steeply sloped (Figure 8 nozzle stove) and a strip of metal
is used to
support the pot the desired channel width from the stove wall,
large
variations in pot size can be accommodated.
Larger pots will sit
further from
the fire, but the decrease in radiant heat transfer will be
in part
compensated by the increased surface area for convective transfer.
RADIATION
All objects
(materials) continuously emit electromagnetic radiation due to
internal
molecular and atomic motion. The higher
the object's temperature,
the greater
the amount of energy so radiated. The
warmth felt on one's
skin when
standing near a fire (but not in the hot gases) is due to
infrared
radiation from the fire. The
temperature of the object can also
be estimated
by its color, ranging from 500[degrees]C when glowing dark red to
800[degrees]C
when bright cherry red to 1100[degrees]C when yellow and to 1500[degrees]C and
more
bse13x52.gif (486x486)
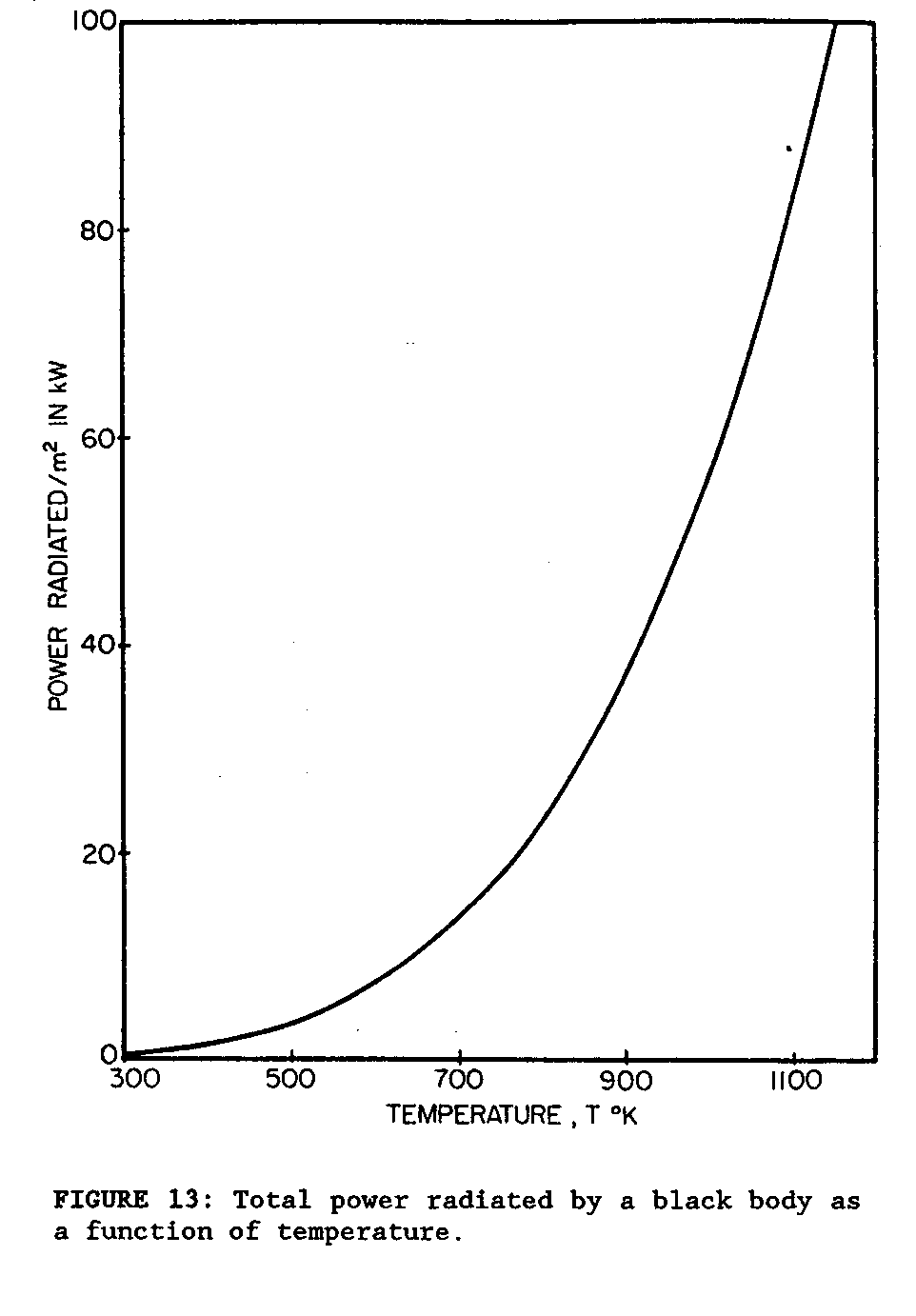
when
white. Figure 13 shows the amount of
energy radiated by a "black
body"
(an object that absorbs or emits radiation perfectly regardless of
wavelength)
as a function of temperature.
Similarly,
all objects absorb radiation, exciting their internal molecular
and atomic
motion. The ability of a specific
material to absorb radiation
is equal to
its ability to emit it.
Most real
materials, however, are not perfect emitters or absorbers.
Metals, for
example, are very poor absorbers (emitters) because the free
electrons
within them that give rise to large electrical and thermal
conductivities
also couple tightly to impinging radiation and screen its
penetration
into the material -- causing it to reflect instead.
Gases such
as water
vapor and carbon dioxide have strongly frequency-dependent
absorption in
the infrared corresponding to excitation of vibrational and
rotational
motion of individual molecules. Typical
emissivities range
from 0.05 for
well polished metals to 0.95 for carbon black.
Table C-1
lists the
(frequency independent) emissivities for a variety of materials.
In
woodburning cookstoves, radiative heat transfer is an important factor
in the
transfer of heat from the firebed and flames to the pot; from the
flames to the
fuel to maintain combustion; from the firebed and flames to
the stove
wall; from the stove wall to the pot; and from the stove wall to
bse2x32.gif (600x600)

ambient
(Figure 2).
In traditional
stoves, typically 10-12 PHU(3) percentage points (out of
perhaps 17
total) are due to radiative heat transfer directly from the
firebed to
the pot bottom (7). This is the primary
heat transfer mechanism
for the
traditional open fire.
Calculating
Radiative Heat Transfer
The radiative
heat transfer from the firebed to the pot is determined by
the firebed
temperature (Figure 13) and by the view factor between the
firebed and
the pot (Figure 14). The view factor is
the fraction of energy
emitted by
one surface that is intercepted by a second and is determined
entirely by
the relative geometry of the two surfaces.
Consider, for
example, a 30 cm diameter pot that is 12 cm above a 15 cm
bse14520.gif (540x540)

so that 57.5
percent of the radiation emitted by the firebed strikes the
pot.
If the firebed is at an average temperature
of 1000 K, Figure 13
shows that it
will emit about 56 kW/[m.sup.2].
Multiplying the firebed area
(0.0752
[m.sup.2]) by (56 kW/[m.sup.2]) and by (0.575) gives the energy intercepted by
the pot as
0.57 kW.
To heat the
pot more effectively by radiation directly from the fuelbed,
the average
fuelbed temperature could be increased (without increasing
fuel consumption).
Alternatively, the view factor could be
increased by
lowering the
pot closer to the fire or increasing the size of the pot
relative to
the firebed.
-----------------------
(3) PHU is Percent Heat Utilized, that is,
the thermal efficiency of the
stove.
This is discussed in detail in Chapter V.
Closing the
firebox and controlling the air supply could increase the
average
firebed temperature but present numerous difficulties in practice.
With the
firebox closed it is difficult to monitor the size and condition
of the
fire. It is also difficult to chop the
wood into sufficiently small
pieces to fit
inside. Finally, many cooks will not
bother to control the
air supply.
Moving the
pot closer to the fire can also increase the radiative heat
transfer from
the fire to the pot as seen in Figure 14.
For example, for
the firebed,
[r.sub.1] = 7.5 cm, the pot [r.sub.2]=15 cm, and the height between them h=15
cms,
[r.sub.2]/[r.sub.1]=2, h/[r.sub.1]=2 and F=0.47.
Reducing the height h to 12 cms, h/[r.sub.1]=1.6
and
F=.57. This is a substantial increase
in the fraction of radiant heat
transferred
from the fire to the pot. Reducing the
height, however, may
interfere
with the combustion processes and increase CO and hydrocarbon
emissions; if
too close the fire will be quenched. In
practice, channel
stoves with
distances as small as 6 cm between the firebed (with a grate)
and a
27-cm-diameter pot have been tested and been shown to give increased
heat transfer
and overall thermal efficiency, but the effect on the
combustion
quality is unknown (20,21). Traditional
artisans have typically
set the
distance between the firebed and pot at one-half the pot
diameter
(22). Until there are reliable
experimental data correlating the
firebed to
pot height with smoke and carbon monoxide emissions, it is
rather
arbitrarily recommended that the pot to grate distance be no less
than 0.4
times the pot diameter.
The effect of
radiative heat transfer from the firebed to the stove wall
and from the
stove wall to ambient temperature has already been modeled
bse4x370.gif (600x600)

and discussed
in detail (Figures 4,5). Similarly,
measuring or calculating
(Appendix B)
the inner wall temperatures enables one to estimate
(Appendix C)
that a metal wall with 2 cm of fiberglass insulation can
provide up to
50% more radiant heat flux to the pot than a bare metal
wall.
The increased radiative and convective heat
transfer possible when
wall losses
are reduced by insulation can substantially increase overall
stove
performance. For example, insulating
the exterior wall of a
prototype
channel stove increased the stove's efficiency from about 33% to
about 41% and
increased its predicted fuel economy relative to the open
fire from
about 48% to about 57% -- a substantial improvement (14).
Using
radiative transfer to heat a pot, as in channel stoves, has both
advantages
and disadvantages. The primary
advantage is that radiative
transfer is
insensitive to the pot shape and depends only on the view
factor
between the firebed and pot(4).
One of the
primary disadvantages of using radiative transfer to heat a pot
is that this
heat loss reduces the average combustion chamber temperature
and can thus
lower the quality of combustion and increase emissions.
Efforts have
been made to avoid this problem by reducing radiative transfer
------------------------
(4) The potential of improved radiative and
convective heat transfer is
indicated by
development work on an advanced gas stove in which efficiencies
of 70% have
been reached with very low outputs of CO and [NO.sub.x] (23).
out of the
combustion chamber to the pot while increasing convective
heat transfer
to the pot in compensation. For channel
stoves, although the
efficiency
could be maintained the same, the increased reliance on convective
heat transfer
reduced the peak fire power that could be reached (24).
For nozzle
stoves, both high efficiencies (43%) and reasonable firepowers
(1-2 kW) have
been achieved in prototypes (18,19), but further development
and testing
is needed before field tests can begin.
COMBUSTION
Biomass
combustion is an extremely complex process and its study involves
chemical
kinetics; conductive, convective, and radiative heat transfer
processes;
molecular diffusion; and other physical phenomena.
Realistic
modeling of
these processes is not yet possible and useful results are
still almost
entirely empirical (25). Thus,
experimental measurements of
biomass stove
performance are always necessary and are discussed in detail
in Chapter
V. Because of the complexity of wood
combustion, the following
will be
limited to a brief and simple description of the chemical and
physical
properties of wood and how it burns. A
somewhat more detailed
description
along with extensive references is given in Appendix D.
As
noted in
Figure 1, however, incomplete combustion typically accounts for
less than 10%
of the energy losses in a stove.
Improving combustion in a
stove is
therefore more important in reducing the health hazard of smoke
than in
increasing overall stove efficiency.
Calorific Values
There are a
variety of ways to evaluate wood as a combustible.
Of the
greatest
practical importance are its calorific value and its moisture
content.
Calorific values are normally expressed as
either gross calorific
value, also
known as the higher heating value, or as the net calorific
value, also
known as the lower heating value. The
gross calorific
value is
defined as the heat liberated when the material is completely
burned to
carbon dioxide and liquid water at 25[degrees]C.
The net calorific
value is the
same except that the water is assumed to remain in the
gaseous phase
(i. e., steam) at 100[degrees]C. For
cookstove designers and
testers, the
net calorific value is the more useful.
As dry wood typically
is about 6%
hydrogen by weight, about 0.54 kg of water will be
produced per
kilogram of dry wood burned. The heat
absorbed to warm and
vaporize this
water will then reduce the net calorific value about 1390
kJ/kg as
compared to the gross calorific value.
Because all
woods are similar in structure and chemical composition, their
calorific
values are likewise comparable. On the
average, dry wood is
composed of
49.5% carbon, 6% hydrogen, 43.5% oxygen, and 1% mineral salts
by
weight. On a dry basis, the gross
calorific value for hardwoods is
about
19,734[-or+]981 kJ/kg (over 268 species) and for softwoods is about
20,817[-or+]1479
kJ/kg (over 70 species). Values for
heartwood, sapwood, and
barks are
within about 5% of these values (26).
The observed
variation among species, given by the standard deviations
above, can be
accounted for by slight differences in the proportions and
calorific
values of the five main wood components: cellulose (17,500
kJ/kg),
hemicellulose (17,500 kJ/kg), lignin (26,700 kJ/kg), resins
(34,900
kJ/kg), and mineral salts (0 kJ/kg) (18).
On the average, woods
are composed
of roughly 40-50% cellulose, 15-25% hemicellulose, and 20-30%
lignin, with
the other components comprising small percentages.
Calorific
values for
other biomass materials are listed in Appendix D.
It is
important to note that although wood densities can vary enormously,
their
calorific value per kilogram does not.
Experimentally, the wood
density does
not appreciably affect stove efficiency (27,28).
However,
for the same
amount of energy, a very large volume (but roughly the same
mass) of low
density woods or biomass materials such as corn or millet
stalks is
required. For a given combustion
chamber volume, low density
fuels will
need to be fed in much more frequently.
Moisture
Content
The second
most important way to evaluate biomass is by its moisture
content.
All biomass contains some water which must
be evaporated before
the biomass
can burn, thus reducing its effective calorific value.
However,
tests have shown that net stove efficiency is improved slightly
if the wood
has a moisture content of 10-20% (28,29).
This may be due to
the moisture
helping to localize the fire and reducing the escape of the
volatiles out
of the combustion zone before they can completely burn (29).
Alternatively,
the water may provide additional OH radicals which assist
combustion.
Moisture
content (M.C.) can be expressed as either a percentage of the
total wet
wood mass (oven dry wood plus water), or as a percentage of the
oven dry wood
mass. These can be written as follows
and are graphed in
bse15x57.gif (540x540)

Figure 15
below (30).
[M.C..sub.wet] = water (kg)/[dry wood
+ water] (kg) x100% = water (kg)/wet wood (kg) x 100%
[M.C..sub.dry] = water (kg)/dry wood
(kg) x100%
Even when
protected from the rain and air dried for a long period of time,
wood and
other biomass can have a large amount of water in them.
The
moisture
content of air dried wood has been estimated to be (31,32):
[M.C..sub.dry] = 0.2 RH
where RH is
the average relative humidity. A much
more detailed analysis
correlating
the moisture content of the wood with both the relative
humidity and
the temperature is given in (32). Thus,
in a tropical area
where the
relative humidity averages 90%, the moisture content by this
equation will
be 18% on a dry basis. This equation is
only indicative at
best,
however. Exposure to the rain, sun, or
numerous other variables can
alter the
moisture content. For best accuracy,
direct moisture content
measurements
should be made by drying the wood in a kiln (Appendix F).
Knowing the
moisture content is important. In
testing stoves the moisture
content
strongly affects the estimated calorific value.
In using stoves,
it strongly
affects the ease of burning. The
moisture content reduces the
effective
calorific value of wood by just 2575 kJ/kg water -- the amount
of energy
needed to raise the temperature of water to boiling and evaporate
it.
This should be compared to an oven dry
calorific value for wood
of about
18000 kJ/kg. However, it dramatically
reduces the apparent
calorific
value based on the weight of wet biomass (Figure 15).
For
example, a
kilogram of wood with a 20% moisture content will have just
(0.8)(18000)-14,400
kJ of energy in it, of which about 515 will be used to
evaporate the
water. Instead of a presumed 18000 kJ
of energy in the
kilogram of
wood, there are only 13,900 kJ. Thus,
field measurements,
which are
normally of only partially dried biomass, will significantly
overestimate
the energy use by a family unless corrections for moisture
content are
made.
Volatiles
A third
manner in which biomass fuels are characterized is by their
volatile
fraction. Wood is typically composed of
about 80% volatile
material and
20% fixed carbon. In contrast, charcoal
produced by traditional
kilns will
typically be 80% fixed carbon and 20% volatiles, with
relative
amounts of fixed carbon and volatiles depending strongly on the
manner in
which it was made, particularly the maximum kiln temperature and
duration at
that temperature (Table D-2).
Other
chemical and physical properties of wood and biomass are discussed
in Appendix
D.
The
Combustion Process
The
combustion of wood and other raw biomass is very complicated but can
be broken
down crudely into the following steps:
o
The solid is heated to about 100[degrees]C
and the absorbed water is boiled
out of the wood or migrates along the wood
grain to cooler areas and
recondenses.
At slightly higher temperatures, water that is weakly bound to
molecular groups is also driven off.
Heat transfer through the wood is
primarily by conduction.
o
As the temperature increases to about
200[degrees]C, hemicellulose begins to
decompose followed by cellulose.
(See Appendix D for a brief description
of these materials).
Decomposition becomes extensive at
temperatures
around 300[degrees]C.
Typically only 8-15% of cellulose and
hemicellulose
remain as fixed carbon, and the remainder
is released as volatile
gases.
Roughly 50% of the lignin remains behind as fixed carbon.
The volatiles produced by this
decomposition may escape as smoke or may
recondense inside the wood away from the
heated zone. This can often be
seen as pitch oozing out the non-burning
end of the wood. Heat transfer
into the wood is still primarily by
conduction, but the volatiles
flowing out of the heated zone carry some
heat away by convection.
o
As the volatiles escape the wood, they mix
with oxygen and, at about
550[degrees]C (27), ignite producing a
yellow flame above the wood. Although
radiant heat from the flame itself (not
counting radiant emission from
the charcoal) accounts for less than 14% of
the total energy of combustion
(33), it is crucial in maintaining
combustion. Some of the radiant
heat from this flame strikes the wood,
heating it and causing further
decomposition.
The wood then releases more volatiles, which burn,
closing the cycle.
The rate of combustion is then controlled by
the
rate at which these volatiles are
released. For very small pieces of
wood, there is a large surface area to
absorb radiant heat compared to
little distance for the heat to penetrate
or for the volatiles to
escape.
Thus, fires with small pieces of wood tend to burn quickly.
This is also why it is easier to start a
small piece of wood burning
than a large thick one.
A thick piece of wood has less area to
absorb
the radiant heat from the flame compared to
the greater distances
through which the heat and volatiles must
pass within the wood and the
larger mass that must be heated.
The temperature of the hot gas above the
wood is typically around
1100[degrees]C and is limited by radiant
heat loss and by mixing with cold
ambient air.
As the volatiles rise they react with other volatile
molecules forming soot and smoke and
simultaneously burning as they mix
with oxygen.
Some 213 different compounds have so far been identified
among these volatiles (25).
If a cold object, such as a pot, is placed
close to the fire it will
cool
and stop the combustion of some of these volatiles, leaving a
thick black smoke.
Overall, these burning volatiles account
for about two-thirds of the
energy released by a wood fire.
The burning charcoal left behind
accounts for the remaining third.
Because the volatiles are released
as long as the wood is hot, closing off the
air supply stops combustion
alone.
The heat output of the fire is then reduced but the wood
continues to be consumed for as long as it
is hot, releasing unburned
volatiles as smoke and leaving charcoal
behind.
o
As the topmost layers gradually lose all
their volatiles only a porous
char is left behind.
This hot char helps catalyze the breakdown
of
escaping volatile gases, producing lighter,
more completely reacting
gases to feed the flames.
In some cases, the volatiles cannot easily
escape through this char layer.
As they expand and force their way out,
they cause the burning wood to crack and
hiss or spit burning embers.
The char layer also has a lower thermal
conductivity than wood. This
slows conduction of heat to the interior
and thus slows the release of
volatiles to feed the flames.
At the surface of the char carbon dioxide
reacts with the char's carbon
to produce carbon monoxide.
Slightly further away (fractions of a
millimeter) the greater oxygen
concentration completes the combustion
process by reacting with the carbon
monoxide to produce carbon dioxide.
The temperature near the surface of the burning
charcoal surface is
typically about 800[degrees]C.
The endothermic (heat absorbing)
dissociation of
carbon dioxide to carbon monoxide and
oxygen, and radiant heat loss,
limit higher temperatures.
When all the carbon has burned off only
mineral salts remain as ash.
This ash limits the flow of oxygen to the
interior and so limits the
combustion rate.
This is an important mechanism controlling the
combustion rate in charcoal stoves.
o
The entire process uses about 5 [m.sup.3] of
air (at 20[degrees]C and sea level
pressure) to completely burn 1 kg of
wood. To completely burn 1 kg of
charcoal requires about 9 [m.sup.3] of
air. Thus, a wood fire burning at a
power level of 1 kW burns 0.0556 grams of
wood/second and requires
about 0.278 liters of air per second.
Additional, excess air is always
present in open stoves and is important to
ensure that the combustion
bse16x60.gif (600x600)

process is relatively complete.
Figure 16 sketches these processes.
A complete
description of the combustion process is further complicated by
such factors
as the inhomogeneous structure of wood and charcoal -- such
as pores,
cracks, wood grain, and anisotropic properties; and the presence
of
moisture. For example, because of the
long fibers and pores running
through the
wood, the thermal conductivity and transport of volatiles is
much easier
along the grain than crosswise. This
assists combustion. In
contrast, the
pore structure is disrupted in briquetted fuels, making them
generally
more difficult to burn.
Improving
Combustion Quality
A variety of
techniques are being developed to improve the efficiency and
the quality
of combustion in stoves. Among them are
the following:
o
Using a grate will often increase efficiency
and may reduce emissions
as well.
Tests of traditional stoves, for example, have shown that the
use of a grate alone could increase the
efficiency from about 18 to
nearly 25 percent (34).
Grates appear to perform several functions
in improving stove performance.
By injecting air below the fuelbed they
provide better mixing of
air with both the fuelbed and the diffusion
flame above -- likely
improving the combustion of both.
This may allow the pot in multipot
and channel stoves to be placed closer to
the fire -- improving radiant
heat transfer -- without significantly
interfering with combustion.
Grates with a high density of holes (high
fraction of open area) can
also achieve high firepowers due to the
improved mixing of air with the
fuelbed (14).
This allows a more localized fire and in multipot and
channel type stoves, better radiant heat
transfer (due to a higher view
factor) to the pot.
In practice, it is important that grates be
frequently cleaned of ashes
so that air flow is not blocked.
o
Controlling excess air can increase
efficiency but may also increase
emissions if too little oxygen enters the
combustion chamber or if the
fuel-air mixing is poor.
Excess air is that which flows into the
combustion
chamber in excess of that needed for
stoichiometric combustion
(Appendix D).
There are numerous practical difficulties in controlling
excess air as well; these were previously
noted under RADIATION.
o
Injecting secondary air into the diffusion
flame may, in some cases,
allow more complete combustion than would
otherwise be possible (35).
(Secondary air is the air that enters the
diffusion flame from above
the fuelbed -- this is in contrast to
primary air which enters the
combustion zone at the level of the
fuelbed, or from below when a grate
is used.) This may be particularly
important when excess air is
controlled.
Where an open firebox is used, however, secondary air may
lower efficiency by cooling the hot gases
(20, 34).
o
Preheating incoming air may also improve the
quality of combustion and
the efficiency by raising average
combustion chamber temperatures.
Preheating, however, can only be done in
stoves where excess air is
controlled; otherwise the air will bypass the
preheating ducts and flow
directly in the door.
Further, to achieve significant preheating
of the
air entering the stove, it is necessary to
pass the air through a
narrow channel bounded by the hot
combustion chamber wall. This is the
exact converse of using the hot combustion
gases to heat the pot.
Preheating in this manner may, however,
cause a significant pressure
drop and reduce the air flow.
In a stove driven by natural convection
this may starve the fire, reduce the peak
firepower possible, or reduce
the pressure available to drive convective
heat transfer to the pot.
Chapter VI discusses the use of preheating
in high temperature furnaces
and the theoretical analysis is presented
in Appendix E.
o
Optimizing the shape of the combustion
chamber may affect the combustion
quality and stove efficiency in a number of
ways. As already
discussed, in multipot and channel stoves,
the height chosen for the
pot above the fuelbed is a compromise
between the radiant heat transfer
to the pot and the combustion quality.
The overall volume of the
combustion chamber may be determined in
part by the type of fuel used.
Low density fuels such as agricultural
waste may need a larger volume
or else require frequent stoking.
Baffles can be added to promote
recirculation of and turbulence in the
combustion gases to improve
bse8x44.gif (600x600)

overall combustion.
The nozzle stove (Figure 8), for example,
uses a
section of a cone just above the fuelbed to
establish zones in which
gases from the edge of the diffusion flame
can recirculate until they
diffuse to the center of the flame and burn
completely. Additionally,
this prototype nozzle stove injects primary
air at an angle to the
combustion chamber to promote swirl and
thus improve fuel-air mixing
(18, 19).
o
Insulating the combustion chamber raises
interior temperatures and can
thus reduce emissions.
With each of
these techniques, a careful balance must be found between the
efficiency,
emissions, ease of use, firepower, and cost.
This balance can
only be
determined by detailed testing as described in Chapter V.
OTHER ASPECTS
OF STOVE EFFICIENCY
There are
several other ways in which fuel use can be reduced.
Among
these are
improving control of the stove, improving the pot, and speeding
up the
cooking process itself.
Control
Efficiency
How well the
fire in a stove is tended can strongly influence fuel use.
In
Burkina Faso,
daily weighing of the fuel during a survey sufficiently
sensitized
the cooks that they reduced fuel consumption by 25% (36).
A typical
cooking process will use high fire powers to bring a pot to a
boil, then
low powers to simmer it. The amount of
fuel used then depends
on both the
stove's and the cook's "dynamic power range" -- that is, their
ability
together to provide a high fire power and then rapidly make the
transition to
a low power as needed, never using more fuel than absolutely
necessary to
reach boiling and then maintain a light simmer.
In simpler
terms, the
stove must be controllable; the cook must, in fact, control it.
Note (42)
discusses control efficiencies in more quantitative terms.
The type of
stove and fuel both influence the potential and manner of
controlling
the firepower. Multipot stoves suffer
because it is impossible
adequately to
control the heat input to several pots from one fire.
A fire
just large
enough to cook the first pot provides insufficient heat to the
second; a
fire large enough to cook the second pot will overcook the
first.
Although this problem can be reduced by
making all the pots the
same size and
thus interchangeable, it cannot be eliminated.
Perhaps only
a single pot
meal is desired, or perhaps a large pot is needed for the
rice and a
small one for the sauce. The precise
demands will change with
every type of
meal. Thus, multipot stoves are
intrinsically less efficient
than single
pot stoves.
Numerous
groups have attempted to circumvent the problem of control by
using
adjustable dampers. However, these tend
to be very difficult to
maintain and
use, are often ineffective, and can considerably alter the
combustion
and heat transfer characteristics to all the pots in the stove,
not just the
individual one for which the damper was intended.
Further,
because of
the circuitous path the gases must then follow through the
stove, it is
often difficult to start a fire.
Certain other
types of stoves are also hard to control.
Stoves that first
gasify the
wood and then burn the gas directly under the pot must heat a
charge of
wood to temperatures as high as 1000[degrees]C and more in a reduced
oxygen
atmosphere. The rate of gas production
is sensitive to this operating
temperature,
yet the temperature is hard to control, let alone
rapidly
increase or decrease as needed for cooking.
Efforts to develop
satisfactory
gasifier type stoves for the individual household have so far
been
unsuccessful due to the difficulty of controlling them (18, 19).
In
contrast,
large gasification systems using coal as a feedstock and piping
gas to
individual households have been in use for many years and are still
being used in
India and China (40). Due to the high
CO content of the gas,
the safety of
gasification systems remains an important issue (41).
Control of a
fire may be assisted by having a stove with a very high
thermal
efficiency. In this case, failure to
reduce the fire power could
cause the
food to burn. Such feedback can
sometimes be an important
element in
sensitizing the cook to controlling the fire.
The control
of a stove also depends on the type of fuel being used.
For
example,
simply cutting the air supply to a wood fire will control the
combustion
and heat output but still allows consumption of the wood by
release of
volatiles as long as the wood is hot.
Therefore, wood fires
should be
controlled by removing the wood from the fire and quickly extinguishing
it.
In contrast, hot charcoal does not release
large quantities
of volatiles
and so cutting its air supply is an effective control.
The condition
of a fuel is also a factor. Wet fuel
burns with difficulty
and may not
sustain a small fire. In this case
reducing the fire power
during
simmering can be difficult. The
unavoidably larger fire then
wastes fuel
and evaporates excessive amounts of water from the food.
A high
quality stove and fuel both assist control of the fire and will
usually each
provide fuel savings. However, taking
best advantage of
potential
fuel savings requires that the cook carefully control the fire.
To do this
close individual follow-up is important:
showing users that
proper
control does save fuel and how to control the fire; that it is not
necessary to
boil the food violently and that a light boil is adequate;
and that even
such simple acts as pushing the wood into the stove when it
begins to
burn outside, or extinguishing it.
Such training
of stove users is a very important aspect of stove dissemination.
One of the
most important factors determining field performance of
a stove is
the fire power it is run at during the simmering phase.
Because
simmering
times tend to be long, quite modest increases in fire power
above the
minimum needed can greatly increase total fuel consumption (Note
42).
There are very good reasons, however, for
sometimes running a stove
at a higher
fire power. When a stove smokes excessively,
increasing the
fire power
will usually reduce this smoke by raising average combustion
chamber
temperatures and improving the quality of combustion.
Users must
then choose
between the discomfort of more smoke while cooking or the
discomfort of
gathering additional fuel. The
automatic reaction of most
is to blow on
the fire, add more fuel, and avoid the smoke.
For many this
becomes a
deeply ingrained habit. When using an
improved stove such a
reaction
should no longer be necessary and users must be retrained
accordingly.
It is not
realistic, however, to expect cooks to control their stoves
perfectly;
they have far too many other tasks to take the time.
A stove
that saves
fuel anyway and that needs little oversight is highly desired.
Further, in
some cases it is not in the cook's interest to use a stove
efficiently.
In Niamey, Niger, for example, hired cooks
traditionally
have the
right to the charcoal remaining at the end of the cooking to sell
or to use for
themselves. In this case there may be
resistance to the use
of an
efficient stove that produces little charcoal or to using it
efficiently.
Pot
Efficiency
Fuel use can
also be reduced by improving the "pot efficiency."
As seen
earlier in
the heat balance for cooking food on a stove, a very large
amount of
energy is lost through excess evaporation (Figure 1).
Use of a
tightly
fitting lid and reducing the excess firepower can therefore
greatly
reduce fuel consumption. Heat is also
lost from the pot lid and
the portion
of the pot exposed to ambient air.
Insulating them can reduce
this loss
(37).
Another
method of improving the "pot efficiency" is to use a "haybox
cooker."
In this case, the pot of food is heated to
boiling and then
quickly
transferred to a highly insulated box.
The food is then cooked by
the
"retained heat," that is, by its own heat, which is held in by the
high quality
insulation of the "haybox" (38).
Finally, the
cooking process itself can be speeded up by use of a pressure
cooker.
Pressure cookers raise the pressure and thus
the boiling temperature
of the
pot. Raising the temperature speeds the
physico-chemical
processes of
cooking. For long cooking times this
may save energy and,
perhaps more
importantly for the cook, can save large amounts of time.
Pressure
cookers may be especially useful at high elevations or in areas
where cooking
times are long.
In closing
this chapter the human element must be re-emphasized.
The goal
of applying
engineering heat transfer to biomass stove design is not an
academic exercise
to determine what the limits in thermal efficiency may
be.
Rather, the goal is to better the lives of
the two billion people who
now use
fuelwood to meet their domestic needs.
Improving stove efficiency
is important
to the extent that it reduces the cost of buying fuel or the
burden of
foraging for it. Improving combustion
is important to the extent
that it
reduces the exposure of women and children to toxic emissions.
Closing
stoves is important to the extent that it prevents burns.
It is on
these human
needs that stove programs must be focused and that the stoves
themselves
must satisfy. In many areas of the
world, there is no likely
alternative
to biomass stoves for the foreseeable future (Table II-19).
Engineering
design, and similarly, anthropology, economics, ergonomics,
sociology,
and many others, are all tools to be used to design, develop,
and
disseminate biomass stoves that truly meet these human needs.
There is
not time to
waste.
CHAPTER IV
STOVE
CONSTRUCTION
In the last
chapter, design principles showed that of the numerous
possible
combinations of stove type(1) (multipot, channel), construction
material
(sand-clay, concrete, metal, ceramic), and fabrication technique
(owner,
artisan, factory), lightweight channel stoves that are mass
produced by
artisans or in factories have the highest efficiency.
Constructing
stoves of lightweight materials at central locations offers a
number of
advantages in addition to potentially high efficiency.
Mass
production
from standardized templates allows all the attendant advantages
of rapid
production, reduced cost, improved quality control, and the
additional
market advantage of a professional finish.
Although assembly-line
production of
stoves generates fewer jobs than individually handcrafting
each, the
increased productivity, reduced training and production
costs, and
generally higher quality will usually more than compensate.
As they are
lightweight, such stoves can be disseminated through the
existing
market system and carried home by the client personally.
This
greatly
simplifies the logistics of stove production and dissemination and
lowers
transport costs of both raw materials and finished products.
Stoves, then,
become a standard consumer product no different than the
pots used on
them or the spoons used to stir the food.
Artisan or factory
produced
stoves, however, do cost money. This
can be a very serious
handicap in
cash poor areas.
In contrast,
due to their fragility, massive stoves of sand-clay must be
built on site
by their owner or by an artisan. Such
stoves offer several
important
potential advantages. They can be
constructed of local materials
----------------------
(1) Nozzle
stoves are not considered in this chapter as, at the time of
this writing,
further development and testing were needed before large
scale field
tests could begin. Interested parties
should contact ASTRA.
(when
available); if owner built with minimal outside supervision
they cost
little or nothing -- a very important asset in rural areas; or
if artisan
built, they provide local employment.
Their potential disadvantages
include often
low fuel economy even compared to the open fire
(Tables V-1,
V-2) due to their large mass and due to dimensional errors in
their
construction; short lifetimes (typically less than two years) due to
cracking in
the heat of the fire or exposure to water; and slow production
(often less
than 1 stove per day per person), among others.
Massive
stoves of concrete could in principle be manufactured at a central
location and
transported to the site rather than being constructed at the
site
itself. This would reduce some of the
problems of quality control
and slow
production but they would still have generally lower performance
and be more
difficult to transport than lightweight stoves.
In attempting
to replace traditional stoves with more efficient designs it
must be
recognized that traditional stoves have a number of positive
attributes
and only with considerable effort will they be displaced.
Traditional
stoves cost little or nothing; they have a long lifetime; and
they are
portable or easily built at each desired cooking location by the
owner or by a
local artisan. They typically have a
respectable thermal
efficiency of
15-19% (1); they adjust to a variety of pot sizes and shapes
with little
change in performance; they are relatively insensitive to
errors in
construction; and they provide light.
When developing improved
stoves it is
necessary to take these advantages as well as many other
factors into
account.
CONSTRUCTION
OPTIONS
A variety of
configurations of lightweight channel stoves are possible,
some of which
are listed below. Detailed testing
techniques in Chapter V
assist the
stove developer to choose among these options on the basis of
efficiency,
cost, ease of use, and other factors.
Wall
Materials
Possible wall
materials include metal, usually sheet steel, and ceramic,
or fired
clay. Insulants include materials such
as fiberglass and vermiculite.
Metal walls
might be alloys, electroplated, or given a heat
resistant
coating to help reduce rust or corrosion.
Electroplating,
certain types
of coatings, or polishing may also give a lower emissivity
surface and
improve market appeal at the same time.
Reducing heat
loss from metal walls was discussed at length in the
previous
chapter. Two possible construction
options, using double or
insulated
walls, are shown in Figure 1. The
slightly tapered insert
fitting into
the combustion chamber alone is particularly appealing due to
its
simplicity. It also helps center the
fire in the combustion chamber.
Ceramic
(fired clay) stoves must be highly resistant to thermal and
mechanical
shock. This requires a careful choice
of refractory clays; the
addition of
materials such as rice husk or powdered pottery shards (grog),
which disrupt
the structure of the ceramic and prevent cracks from
propagating;
and good firing. In some cases it may
be desirable to pack
mud around
the stove. Although this may lower the
performance of the
stove
somewhat by increasing the mass of its wall and will reduce its
portability,
it may significantly increase the lifetime of the stove by
reducing the
thermal stress on its wall. (When the
exterior is packed in
mud, the
temperature change across the fired clay portion of the wall is
less than in
the case when the exterior wall is directly exposed to
ambient
air. This reduces the stress on the
wall due to temperature dependent
thermal
expansion.)
The choice of
channel gap and length must be based on the need for efficiency,
high fire power,
and low cost (long channels require more material).
The choice of
channel gap must also, in part, be based on the local
ability to
maintain precise dimensions. For
example, beginning with a 6-mm
channel, a
2-mm error (i.e. , to 4 mm) might result in a stove that would
not heat
well. This could seriously damage the
credibility of a stove
program.
In contrast, beginning with an 8-mm channel,
a 2-mm error (i.e.
to 10 mm)
could lead to a lower efficiency stove but it would still work.
Similarly,
the choice of channel gap will depend on how the stove is
maintained.
If soot is allowed to build up, or the pots
are coated with
mud, the
channel gap will be reduced and the stove may not work.
Stove Shapes
The type of
material used and the choice of channel length will, in part,
also be based
on the pot shape. For example, a
cylindrical stove made of
fired clay
may easily break because the forces on it from the pot are
expansive or
shear rather than compressive; a contoured form is preferred
bse2x69.gif (600x600)
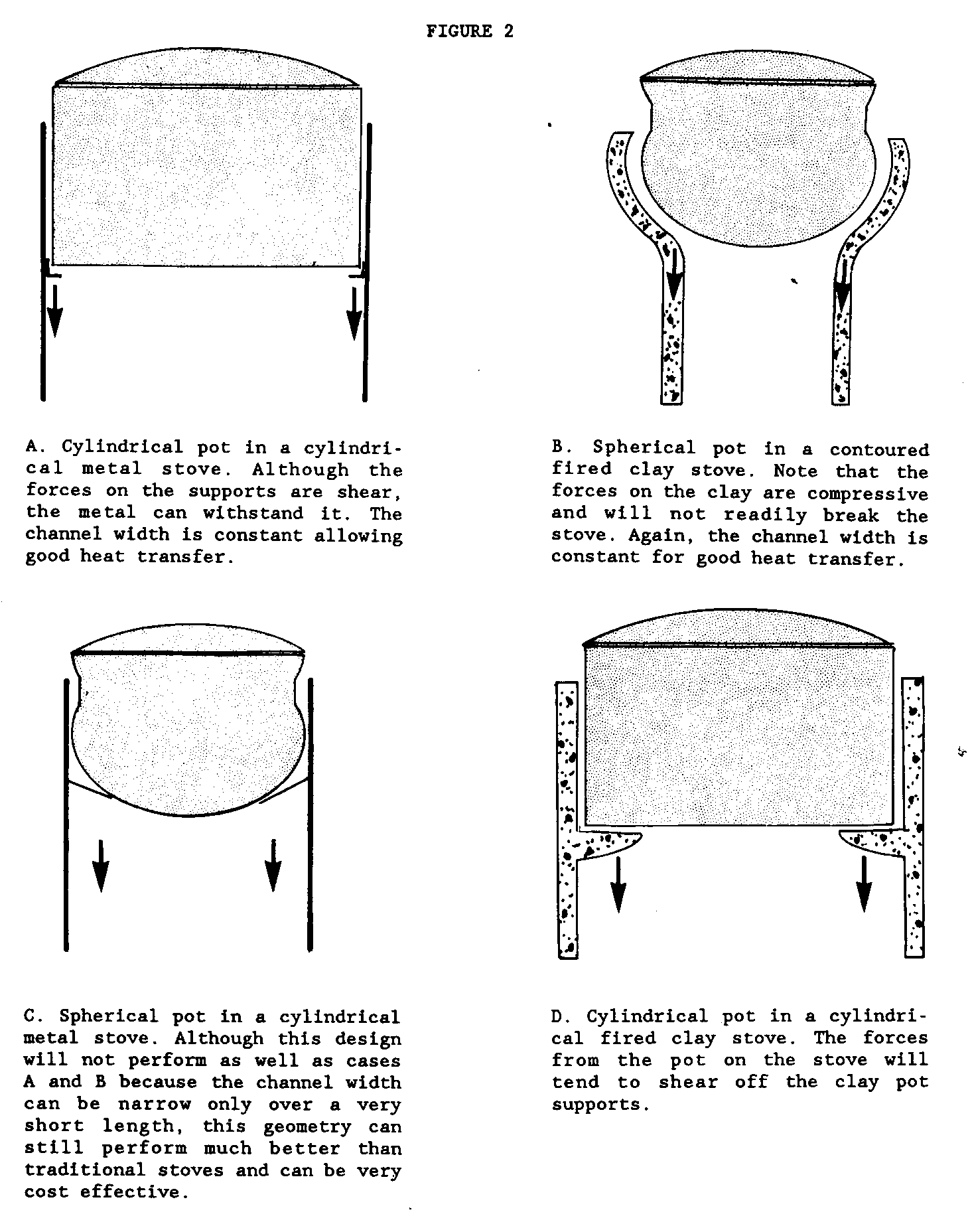
(Figure 2) and
can be formed rapidly.
In contrast,
forming a contoured stove from sheet metal, though possible,
requires
expensive spinning or stamping equipment and dies.
The increase
in
performance, even over a spherical pot in a cylindrical metal stove,
may not be
worth the increased cost and production difficulty (Figure 2).
In
considering a spherical pot in a cylindrical stove it should be noted
that the
channel gap varies continuously, and that its narrow portion,
where the
greatest heat transfer takes place, is very short.
Such a short
section can
give high efficiency if very narrow, but this strongly limits
the fire
power and total heat flux to the pot.
Lengthening the channel is
ineffective
as the gap becomes increasingly large.
High efficiencies at
reasonable
firepowers have been achieved with this combination of pot and
stove shape
nonetheless (Table V-1).
Another
important factor in construction is that the stove must be truly
round and the
pot properly centered. In places where
the channel is wider
than average,
such as a deformed ceramic wall or where a metal wall is
welded or
folded together, excessive heat can flow out, lowering the
efficiency.
Figure III-9 and Table B-4 demonstrate this
point in detail.
One should
therefore pay particular attention to the manner and the
precision
with which the wall is formed and to use tabs to center the pot.
Supports that
rest against the wall of a metal stove may also push the
wall outwards
under the weight of a heavy pot, deforming the wall and
bse3x700.gif (600x600)

allowing excessive
heat loss at these points (Figure 3).
To reduce
smoke levels and improve cleanliness in the kitchen, chimneys
bse4x71.gif (486x486)

are an option
that should always be considered and encouraged.
The same
design
principles apply as before, with the important addition of a gas
manifold at
the top of the stove to allow gas to flow freely around the
pot before
exiting out the chimney. In addition,
the chimney should have
a break in it
and be open to room air at a point somewhat above the stove.
This will
prevent the chimney from drawing too much draft through the
stove
following a reduction in the fire power while the chimney is still
hot.
It is also important that the design include
provision for cleaning
the
chimney. Cleaning must be done
periodically to prevent creosote and
soot build-up
inside the chimney from creating a fire hazard.
Cooks often
prefer spherical pots as there are no corners for food to get
stuck in and
the lip helps curl the food back in when mixing.
Stoves with
chimneys,
however, may need a very wide top rim on such pots for them to
fit on the
stove and not fall in. Traditional
green sand casting techniques
are usually
unable to cast such a wide flat surface and thus
present a
bottleneck for their introduction with chimney designs.
Accessories
Other
possibilities to improve the usefulness of a stove include clamps to
hold the pot
or stove more rigidly when mixing foods.
This might take the
form of bars
or a forked stick placed through the pot handles and held
down by a
foot to fix the pot and stove together into place.
For use on
sandy soils,
the stove can be given a wider base to help stabilize it or
to prevent it
from sinking into the ground. A hole at
the center will
allow the
ashes to fall out so that the stove is cleaned automatically
when
moved. Alternatively, a removable ash
tray could be placed below the
grate.
Handles are also often useful additions,
particularly for stoves
that run hot
such as those with single bare metal walls.
Numerous other
options are,
of course, possible and are limited only by the ingenuity of
the designer
and their utility to the user.
TEMPLATE
DESIGN: CYLINDRICAL STOVES
Template
design for a cylindrical, open firebox, channel type metal stove
is
straightforward. Such stoves are best
used with cylindrical pots, but
have also
been used with spherical pots with good results.
Dimensions
listed below
are nominal and need to be optimized through laboratory
testing.
Laboratory and controlled cooking test data
for this type of
stove are
given in Tables V-1 and V-2.
1.
The width of the cylindrical stove template
is given by
bse72.gif (486x486)

W = C + 2[pi]G + [O.sub.s] + [pi]S
<see figure 1>
where C is
the measurement of the pot around its widest circumference.
G
is the
desired pot-to-wall channel gap. For a
gap of 4 mm, 2[pi]G=2.5 cm; for
6 mm,
2[pi]G=3.8 cm; for 8 mm, 2[pi]G=5.0 cm, and so on.
[O.sub.s] is determined by
the amount of
overlap in the seam. It is preferable
to weld the stove
together end
to end (thus [O.sub.s]=) to prevent the creation of a small
vertical
channel by which the heat can bypass the pot.
If the seam is
crosswelded
or folded, typical values for [O.sub.s] will be 1 cm. S is the
thickness of
the metal used. One typically uses 1 mm
([pi]S=0.3 cm) or 1.5
mm
([pi]S=0.47 cm) thick metal. Thus, for
a 90-cm-circumference pot, a 6-mm-channel
gap, an end
to end welded seam, and 1-mm-thick metal:
W = 90 +
2[pi](0.6) + [pi](0.1) = 90 + 3.8 + 0.3 = 94.1 cm
2.
The template height H is determined by the
sum of the airhole height A,
the grate-to-pot
height P (measured from the top of the grate), and the
channel
length L or, for spherical pots, the amount necessary to extend a
few
centimeters above the pot's maximum circumference.
For cylindrical
bse73a.gif (437x437)

pots, L is
determined by the desired channel length (chapter III) <see figure 2>
H = A + P + L
Typical
values for A are 3 to 5 cm and for P, 0.4 of the pot diameter.
For small
cylindrical pots the height L is typically 5 to 10 cm.
Larger
institutional
or industrial stoves may
have channel
lengths L of 50 cm and
more.
The best height L is determined
more
precisely by comparing the
increased
efficiency and reduced fuel
use caused by
the additional height
versus the
increased cost of the extra
metal.
Additional height can also be
provided at
the top and bottom of the
template,
typically 1 cm each, to allow
the edge to
be folded over to protect
against cuts
on the sharp edges and to
increase the
stove's rigidity and
bse73b.gif (393x393)

strength.
<see figure 3>
3.
Stoves should have a total
air inlet of
at least half the
area of the
pot to wall channel
gap.
For the above stove 94 cm
in
circumference and with a gap
of 6 mm this
is 56 [cm.sup.2]. A
convenient
size, then, is to
have four
airholes, about 3 cm
by 4 cm each
(A=3 cm) or 48 [cm.sup.2]
in area,
spaced symmetrically
around the
stove, but far
enough away
from the door and
the seams to
avoid weakening
the
wall. The airholes are cut
on two sides
only so that when bent upward and inward they can act as
supports for
the grate. Larger airholes may be
necessary if large
pots are used
or if the stove is used on soft soil where the stove
will sink
into the ground and block the airholes.
Alternatively, for
soft soil
conditions a ring-shaped platform can be cut and attached
bse73c.gif (353x353)

to the stove.
<see figure 4>
A fifth
airhole (tab) can be cut opposite the door and bent to be above
the
grate. This will prevent the grate from
tipping upwards when wood is
pressing down
too heavily at the doorway.
4.
Pot supports are similarly spaced evenly
around the stove, but offset
from the door
and edges so as not to weaken the wall.
The height P for
the pot
supports above the top of the airholes (where the grate will rest)
is given
roughly by
P = 0.4C/[pi] = 0.4D
where D is
the pot diameter. The best distance
will vary somewhat with
the size of
wood used locally, its moisture content, and other factors. <see figure
5>
bse74.gif (317x486)

Pot supports
should support the pot stably, yet be small in area so as not
to shield the
pot from the hot gases -- reducing heat transfer.
Pot
supports
should not cause the stove wall to bend when heavily loaded as
this can
change the effective channel width and reduce performance.
5.
The size of the door is somewhat arbitrary
and is determined in part by
the locally
available wood size. Typical door sizes
for use with a 90-cm-circumference
pot are 12 cm
wide by 9 cm high. The bottom of the
door is
placed at the
grate position -- the top of the airholes.
The top of the
door is made
several centimeters below the bottom of the pot so that the
hot gases are
guided up around the pot rather than out the door.
If
necessary,
the door height can be decreased to ensure that it is below the
bottom of the
pot.
6.
The grate is a circle of sheet metal cut to
fit snugly into the
finished
cylinder. Recuperated scrap metal is
often used. The center
half diameter
is punched with a 30% hole density of 1 cm holes.
Grates
should not
have any holes much larger than 1 cm in diameter, since large
holes in the
grate will allow the charcoal to fall through and burn below
the stove,
reducing efficiency. Holes
of too small
a diameter will easily
clog and
reduce air flow into the
bse75a.gif (256x256)
charcoal bed.
<see figure 6>
In some cases
it may be useful to form
a conical
grate. This will both better
localize the
fuel to improve combustion
and provide
an insulating dead air
bse75b.gif (230x230)

space along
the stove wall. <see figure 7>
7.
Spacers, used to center the pot
evenly, are
also often needed. <see figure 8>
bse75c.gif (256x256)

Templates for
tapered pots can be developed geometrically from conic
sections.
Dimensions are developed in the same manner
as above. Other
features such
as double walls, insulation, chimneys, or others can be
included as
desired. Attachments might include
handles for carrying the
stove or
clamps for holding the pot firmly in place while stirring thick
porridges.
METAL STOVE
PRODUCTION
Production
test data for this type of stove, including production rates
and costs,
are given in Tables V-3 and V-4. The
general procedure used is
the
following, with specific tasks divided among different workers.
1.
The template is traced out on the
bse76a.gif (437x437)

metal sheet
as shown in Figure 1 and
cut out in
outline. The door and pot
support holes
are cut out, and the
strips for
the airholes and to support
the grate are
cut.
2.
The metal is rolled into a cylinder -- it
should be as smooth, round,
and straight
as possible. If a sheet metal roller is
used, the top and
bottom can be
folded over before rolling. If bent by
hand, they can be
folded after
rolling. This provides additional
rigidity and prevents the
bse76b.gif (393x393)
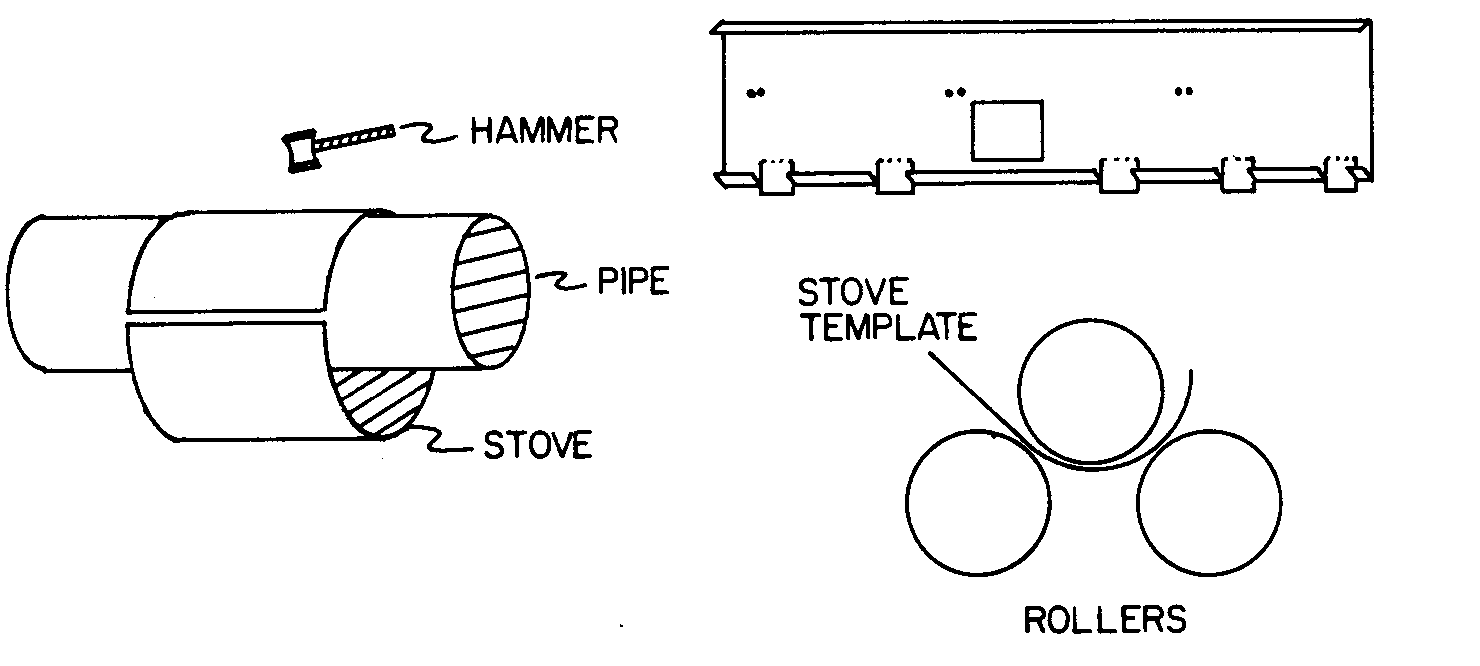
user from
being cut on sharp edges. <see figure 2>
3.
Other components such
as the pot
supports and
the grate are
cut out
and the holes
punched in
bse77a.gif (317x317)

the grate.
<see figure 3>
4.
The stove is welded together and pot
supports are
welded into place. Alternatively,
the stove
walls can be locked
bse77b.gif (256x437)

together by
folding. <see figure 4>
5.
The grate is placed in the stove, and the
tabs for the
airholes are bent inward and
upward to
support the grate. Pot supports are
slid and
folded or welded into place.
6.
The stove is given the desired surface
finish (electroplating, painting
with heat
resistant paint, etc.) to improve its rust resistance and market
bse74.gif (317x437)

appeal, and
to reduce its heat loss by lowering its emissivity. <see figure 5>
bse77c.gif (285x393)

FIRED CLAY
STOVE PRODUCTION
Artisanal
production techniques can produce durable, highly efficient, and
very low cost
fired clay stoves at a rapid rate. To
do so, however,
requires very
careful attention to and painstaking quality control at each
step of the
production process. The optimal mix of
clays must be chosen
to ensure
durability and to provide a high level of mechanical and thermal
shock
resistance. Preparation of the clay
(grinding, pounding) and the
proportion of
water added must be standardized to ensure a uniform
product.
Templates must be carefully sized to take
into account the
shrinkage of
the clay during drying and firing while maintaining the
desired pot
to wall gap, etc. (Shrinkage is most
easily determined by
rolling long
rods of clay; measuring their length when wet, dry, and
fired; and
calculating the percentage change).
Finally, the optimum
firing
techniques and temperatures must be determined.
Each of these
steps requires careful testing and optimization.
The
overall
effort required usually limits production to centralized large-scale
facilities;
only the most highly skilled potters could potentially
produce
quality fired clay stoves on their own.
Within these constraints,
however,
fired clay stoves may be an important alternative for potters who
are losing
their traditional markets.
The
production steps using traditional West African pot production
techniques
are described below. Typical production
costs are given in
Table
V-5. Alternatively, casting, throwing
(on a potter's wheel) or
other techniques
could be used instead. In particular,
the use of
internal
molds (which are interlocking and can be disassembled internally)
and potter's
wheels have been used with some success in Thailand (2).
Flywheel
presses (3) or hydraulic presses used with internal molds may be
even better
(2).
1.
Clays are mined, prepared, mixed, etc.,
according to the need for
durability,
firing, thermal shock resistance, and other factors.
Grog
(finely
ground pottery shards), rice husk, or other materials are often
added to
improve durability. These inclusions
prevent cracks from
propagating
in the finished product.
bse78.gif (285x285)

2.
The clay is kneaded, rolled, and
flattened. <see figure 1> Dried,
powdered clay can
be used to
reduce the surface stickiness of the wet clay.
As the clay is
worked, air
pockets are lanced and bled out.
Flattened, the clay should
be a uniform
thickness, perhaps 2 to 3 cm thick or as needed for durability,
etc.
A template is used to cut out a rectangle of
clay that is
then rolled
into a cylinder and the ends melded together.
This cylinder
forms the
combustion chamber of the stove and its dimensions must be
chosen
accordingly, taking into account such factors as the desired grate
to pot height
of 0.4(pot diameter), and the need to place the combustion
chamber walls
directly under the pot so that the walls are under compressive
rather than
expansive forces, yet without the wall obscuring too much
bse79a.gif (285x285)

of the pot
from direct radiant heat transfer from the firebed. <see figure 2>
3.
More clay is kneaded, rolled into a
ball, and
somewhat flattened into a
circle.
This is then placed in an
appropriately
sized spherical mold and
continuously
turned (using lots of
dried,
powdered clay) and worked to
form the
upper part of the stove. The
dimensions
are checked frequently with
bse79b.gif (317x317)

a template to
ensure accuracy. <see figure 3>
4.
The spherical
section is
placed
on the
cylinder,
the center of
the
spherical
section
is cut out,
and the
two are
melded
bse79c.gif (256x256)

together.
<see figure 4>
5.
Small pot supports, 6-8 mm thick or as
desired and 2-3 cm square, are
placed in
line with the cylinder so as to direct the pot weight downward.
Such supports
are most easily melded to the stove by lightly scratching
and
moistening the mating surfaces.
6.
Supports for a metal grate are added
at the bottom
of the stove.
7.
The doorway is cut out.
Holes for
air flow
under the grate are cut out.
Cuts should
be rounded; sharp corners
tend to
generate greater stress and
bse80a.gif (285x486)

more frequent
breakage. <see figure 5>
8.
All the surfaces of the stove, especially
those cut, are lightly
bse80b.gif (317x317)

moistened and
smoothed to reduce cracking. <see figure 6>
9.
The stove is placed in a cool location and
allowed to dry slowly over a
several week
period. Finally, the stove is fired in
a kiln.
10.
A metal grate is fitted to the stove.
CHAPTER V
STOVE TESTING
In this
chapter laboratory, controlled cooking, production, field, and
marketing
tests are described in detail.
Techniques for financial and
statistical
analysis of the data are presented in Appendixes F and G.
In
areas where
surveys or other analysis have demonstrated the need for safer
and more
efficient biomass burning stoves, tests such as those described
here are
essential for their development.
In brief, the
total testing program recommended is this:
o
Laboratory and controlled cooking tests are
used to select particularly
promising stove prototypes and to optimize
their dimensions.
o
From these tests standard templates are
developed that conform to the
local pot sizes and shapes.
o
A production test is run with these templates
producing 50-100 or more
stoves for each of the most popular pot
sizes. During this production
test a detailed analysis is performed of
the costs, problems encountered
and potential improvements in the
production method.
o
Some of these stoves are then distributed on
a short-term, temporary
basis to selected families for field
testing to determine both their
acceptability and their actual measured
performance in day to day use.
Another portion of these stoves is put on
display in local commercial
outlets and sold on a commission
basis. Such simultaneous marketing
allows some indirect feedback on how
neighbors of the selected families
perceive the stove's potential.
o
On the basis of the production and field
testing results, modifications
can be made to the templates and production
system as needed and the
process repeated.
A similar laboratory, production, field, and market
testing effort can be used for commercial
or industrial applications.
o
When a suitable model has been developed and
fully tested in the field,
larger-scale dissemination can begin.
Various marketing techniques
such as radio and newspaper advertising,
public demonstrations at
social centers, and others can be done.
o
As interest develops, the stove promoter can
gradually withdraw from
the role of commissioning both production
and sales, leaving the stove
producer in direct contact with the various
commercial outlets.
Increasing
the fuel efficiency and safety of a stove may require the
concession of
some of the advantages of traditional stoves, particularly
their lower
initial cost, their flexibility to fit different pots, and the
lighting they
provide. As fuel costs rise, however,
improved stoves will
become
increasingly attractive. Detailed
testing, as described below,
permits the
determination the performance and attractiveness of a particular
stove at any
particular time in any given area.
Further, such
testing
provides a means to launch rudimentary mass production, marketing,
and
dissemination.
The testing
of improved stoves, however, is not an end in itself.
It is
only a means
to developing stoves that save users time, money, and labor,
and protect
their health and safety.
LABORATORY
TESTS
In recent
years a variety of laboratory testing methods have been used.
All of these
methods simulate the high power (to bring to a boil)/low
power (to
simmer) process of cooking while using water to simulate food.
The stove's
performance is measured by its Percent Heat Utilized, PHU, or
by its
Specific Consumption, SC. The PHU of a
stove is the percentage of
heat released
by the fire that is absorbed by the water in the pot.
The
SC is the
total quantity of wood used for the simulated cooking process
divided by
the amount of water "cooked."
Results from different tests of
this general
type are similar but not always precisely comparable.
The
Provisional Draft International Standards developed in December 1982
standardize
this type of method (1). The procedure,
as updated since, is
listed below
(2) and a discussion of useful laboratory equipment is given
in Appendix
H. A more detailed discussion of the
relative merits of
different
testing methods is given in Note (2).
Lab Testing
Procedure
1.
The test conditions are recorded including
air temperature, wind, and
relative humidity.
The stove and pot(s)(1) are described and
sketched in
detail including careful measurements of
their relevant dimensions.
These dimensions should include the grate
to pot and pot to wall
distances when the pot is in place on the
stove.
----------------------------
(1) The (s) in pot(s) and (first) pot in
point 5 refer to the testing
of multipot
stoves.
2. A quantity
of wood no more than twice the estimated amount needed for
the test is weighed, the weight recorded,
and the wood set aside. The
moisture content and calorific value of the
wood should be known.
Testing standards for measuring the
specific gravity, moisture content,
ash, volatiles, and calorific values of
wood or related materials are
given elsewhere (22).
If possible, the wood should be of the same
species and relatively uniform in
size. Buying sufficient wood of the
same species for all the tests and then
storing it in the same well
protected location will aid in maintaining
the moisture content at the
same value.
Periodic rechecks will still be necessary.
3. The pots
should be scrubbed clean both inside and out, and thoroughly
dried before each test.
The pots must be identical in shape and size
for all the tests to prevent these factors
from skewing the test
results.
The dry pot(s) and thermometer(s) are weighed together.
Then
a fixed amount of water is added to the pot(s)
that is roughly equal to
two-thirds of the pot(s)'s capacity but
exactly the same for each test
for all the stoves, i.e., 5.000 kg.
The pot(s) with water and thermometer
is weighed.
The water temperature should be within a few
degrees of ambient air temperature.
Lids should not be used at any
time (Note 2).
4. High Power
Phase: The stove must be at room
temperature. Then, the
fire is lit in a reproducible manner (i.e.,
by using a measured amount
[5 ml] of kerosene), the pot(s) is quickly
placed on the stove, and the
(first) pot is brought to a boil as rapidly
as possible without being
excessively wasteful of heat.
Water temperatures are recorded every
five minutes.
Actions to control or relight the fire, observations of
excessive smoke, high wind, or any others
should also be recorded.
5. When the
(first) pot comes to a full boil the water temperatures and
time are recorded.
Then the following are done rapidly:
o The wood is removed from the stove, any
charcoal is knocked off, and
all of the wood is weighed.
o The charcoal is weighed.
With a large capacity balance and a
lightweight
stove, it is often easier to weigh the
stove empty before the
test, and then weigh the stove with the
charcoal in it to determine
the charcoal weight.
This speeds the process and reduces the
disruption
of the fire.
o The pot(s) with water and thermometer(s)
is weighed.
6. Low Power
Phase: The charcoal, wood, and pot(s)
are returned to the
stove and the fire relit.
The fire is then maintained for 30 minutes
at the lowest power possible that is
sufficient to keep the water
preferably within 2[degrees]C (and not more
than 5[degrees]C) of boiling yet not
boiling excessively.
Water temperatures are again recorded every
five
minutes along with any actions to control
the fire or observations. As
before, no lids are used at any time.
7. At the end
of this 30-minute period of simmering, the wood, charcoal
(or stove and charcoal together), and
pot(s) with water are again
weighed and the values recorded.
8. Finally,
the following indices of stove performance are calculated.
Firepower = P = [M.sub.w] [C.sub.w] -
[M.sub.c] [C.sub.c]
-----------------------------------------
(kilowatts)
60I
where [M.sub.w] is the mass of dry wood
burned, [C.sub.w] is the calorific value of
the dry wood in kJ/kg. [M.sub.c] is the net
increase or decrease in charcoal
and [C.sub.c] its calorific value in
kJ/kg. I is the length of time in
minutes.
The specific consumption is given by
[M.sub.w] - 1.5[M.sub.c]
SC = ------------------------
[W.sub./f]
where [W.sub.f] is
the mass of the water remaining at the end
of the period.
It is often more convenient to express this
as grams wood equivalent
consumed/kilograms water cooked rather than
kg wood/kg water (3).
If there is a large variation in starting
water temperature from day to
day, the SC can be normalized by water
temperature (23). That is,
SCN =
[M.sub.w] - 1.5[M.sub.c]
------------------------------------
[W.sub.f][([T.sub.f] -
[T.sub.i])/75]
Finally, the PHU can be calculated using
4.186[W.sub.i]([T.sub.f]-[T.sub.i])+2260([W.sub.i]-[W.sub.f])
PHU =
--------------------------------------------------------------
[M.sub.w][C.sub.w]-[M.sub.c][C.sub.c]
where [W.sub.i] is the mass of the water in
kilograms at the start, ([T.sub.f]-[T.sub.i]) is
the temperature change of the water in
degrees celsius during that
period, and ([W.sub.i]-[W.sub.f]) is the
mass of the water evaporated. The factor
4.186 kJ/kg[degrees]C is the specific heat
of water, and the factor 2260 kJ/kg
is the latent heat of vaporization of
water. Additional terms are
added as needed for multipot stoves.
Typically, a
minimum of four tests per stove will be necessary.
The test
procedure
should then be repeated as needed to provide statistically
significant
data as discussed in Appendix G.
Laboratory
Test Precautions
In performing
laboratory tests there are a number of cautions:
o
Considerable time and effort must be spent with the people doing the
testing to ensure that the procedure is
followed correctly and consistently,
and that the data are accurately
recorded. It is frequently
useful to design double checks into the
procedure in order to catch
common errors such as misweighing the wood
or incorrectly recording the
values.
As an example, under "remarks" on the sample laboratory test
data sheet, all weights of the individual
pieces of wood added to the
fire can be recorded.
These values can be compared with the totals
to
ensure no wood was lost and no weight
misrecorded. If there is doubt
about a measurement it should be discarded.
o In varying
one parameter, it is vital that there be no other differences.
Thus, in testing the effect of the channel
length on performance,
the different stoves must have identical
diameters, grates, and
doors, etc.
This is crucial.
o Testing
should be done in an enclosed or well protected area to reduce
the effect of the wind.
Even small amounts of wind can appreciably
affect the results -- particularly for open
fires and traditional
stoves.
o If there is
more than one tester, each person should test each stove
the same number of times to eliminate any
bias.
o The order
of testing the stoves should be completely random.
Otherwise,
for example, there will be a tendency to
consistently test stove
A in the late morning when the air is calm
and stove C in the late
afternoon when the wind is blowing strongly
or to do all the tests of
stove A first during a dry period and all
tests of stove C later when
the rainy season begins.
Using a random testing order will reduce
such
potential biases.
o High
altitudes will have a small effect on water boiling tests, and
will have a large effect on field tests due
to the longer cooking times
at the lower boiling temperatures due to
lower atmospheric pressure.
Design
Parameters to be Tested
A number of
parameters that should be investigated in performing lab
bsex870.gif (600x600)

tests,
including the following: <see worksheet 1>
o The channel
gap, length, and shape, and the manner of its fabrication,
such as overlapped or butt-welded
joints. These affect convective heat
transfer.
o The
grate-to-pot height. These affect
radiant heat transfer and
combustion quality.
o The hole
density (the fraction of open space) in the grate, the shape
of the grate (conical to center coals and
fuel, holes only toward the
center, etc.), and the type of material used
for the grate. The hole
density affects the possible firepower and
the thermal mass and insulation
of the grate partially control the heating
rate and efficiency.
o The type of
insulation and how it is placed (over the entire outside,
inside the combustion chamber only, etc.),
or the use of double walls.
These are important in determining both the
overall heat loss through
the walls and, to a lesser extent, the
radiant transfer to the pot and
the combustion quality.
The size, shape, and insulation of the
combustion chamber are also important
considerations. A smaller chamber
may allow higher average temperatures and a
higher chamber may allow a
longer residence time -- both assisting more
complete combustion.
o The control
of primary or secondary air. These may
affect the combustion
quality in some cases.
o The size
and shape of the doorway, or the use of a closeable door or
flapper for air control.
These will help determine the ease of use of
a
stove, e.g., ease of loading, monitoring the
fire, etc.
o The type,
size, and shape of pot supports. Large
pot supports will tend
to screen the pot from the fire but may
support the pot more stably.
o The use of
various types (heights, widths, contours, etc.) of baffles
to improve convective heat transfer or to
cause recirculation in the
combustion zone to improve combustion.
o The use of
various heights, diameters, and materials for the chimney.
o The pot
shape and material.
o The
performance of the system with scale changes (e.g., doubling of the
pot and stove size).
In planning a
series of lab tests, it is often useful to do a few dozen
preliminary
tests in order to determine the actual situation and the
desirable
range of the parameters to be tested.
Once the parameter range
is determined
the testing can begin. Testing is most
often done by
varying one
parameter, such as the channel gap, at a time.
In rare cases,
carefully
controlled factorial type experimental designs can be followed
which allow
several variables to be varied simultaneously.
An example of
such an
experimental design would be to vary the channel gap and length
simultaneously,
as discussed in Appendix G.
Data Analysis
To analyze
the data, the averages, standard deviations, and confidence
limits are
calculated for each type of stove or variation.
The t-test is
used to
differentiate between stoves. Finally,
regressions are used to
determine the
influence of any particular parameter being varied.
Following
extensive laboratory testing, several models are selected for
controlled
cooking tests. The models chosen,
however, should not just be
those with
the lowest SC or highest PHU. In some
cases, these performance
indices may
not correspond to the actual cooking process or may be
misleading.
Thus, stove models covering the entire range
of performance
are selected
foor both controlled cooking tests and field tests.
With
those
additional results the usefulness of the laboratory indices, PHU and
SC, can be
determined and modified as needed.
Similarly, the laboratory
procedure
itself can be modified to better correspond to actual cooking.
Both the PHU
and SC appear to be fairly reliable laboratory indicators of
a woodstove's
field performance (5,6).
TABLE 1
Laboratory Tests of Woodstoves
PHU
PHU
PHU PHU
# of
Stove
POT 1
POT 2
POT 3 Total
Tests
Traditional
Stoves (one pot):
Three Stone
Fire 17.0
17.0[- or +]1.0
9
Metal
"Malgache" 18.2
18.2[- or +]1.3
9
Metal "
" with grate 24.7
24.7[- or +]1.7
6
One-Pot
Massive Stove with Chimney:
Nouna 31
16.9
16.9[- or +]1.0
10
Two-Pot
Massive Stoves with Chimneys:
AIDR 2
15.8
5.8
21.6[- or +]1.0
10
CATRU
14.3
6.1
20.4[- or +]5.3
8
Kaya 2
13.6
6.2
19.8[- or +]1.9
10
Nouna 2
15.2
6.9
22.1[- or +]1.5
10
Nouna
3/2 16.3
5.1
21.4[- or +]1.0
10
Titao
11.2
4.2
15.4[- or +]0.9
10
Three-Pot
Massive Stoves with Chimneys:
AIDR 3
14.8
4.5
2.5 21.8[- or +]0.8
10
Kaya 3
10.2
5.9
4.0 20.1[- or +]1.6
10
One-Pot
Massive Chimneyless Stove:
Louga
19.0
19.0
n.a.
Two Pot
Massive Chimneyless Stove:
Banfora
18.8
7.9
26.7[- or +]1.3
10
One-Pot
Lightweight Chimneyless Channel Stoves:
Metallic(*)
29.1
29.1[- or +]:1.3
10
Ceramic(**)
31.9
31.9[- or +]2.2 10
Ceramic(**)long
channel 36.1 36.1[-
or +]1.9 14
Insulated
Metal(*) 42.6
42.6
n.a.
References
(5,7,8,9). Note that values here are
recalculated from
reference (5)
and include charcoal. All pots were
spherical.
(*)
cylindrical stove. (**)spherical stove.
Examples of
laboratory test data are given in Table I.
In particular, the
relatively
low performance of the massive and multipot stoves compared to
the
lightweight channel stoves should be noted.
This corresponds to the
theoretical
analysis presented in Chapter III.
Additional preliminary
test data
showing the influence of channel gap and of insulation on the
performance
of lightweight channel type woodstoves are given in (9).
Although not
discussed here, the measurement of stove emissions is as
important as
the measurement of efficiency. Readers
are strongly urged to
contact the
East-West Center in Honolulu, Hawaii, for information on
emission
testing methods.
CONTROLLED
COOKING TESTS
Controlled
cooking tests (CCTs) are useful in demonstrating that the model
stoves are
easy to use and perform well in actual cooking.
In addition,
they help
verify that laboratory tests are measuring parameters relevant
to actual
cooking. Although they are more
difficult to conduct than
laboratory
tests, they are an important intermediate step before production
and field
testing are begun.
The general
steps for performing controlled cooking tests follow.
1. A standard
meal, typical for the area, is chosen and several tests are
performed in order to standardize precisely
the type and quantity of
each ingredient.
Standardizing quantities prevents the occasional need
for excessive boiling to eliminate extra
water that might have been
added by mistake or perhaps consistently by
just one of the cooks.
Standardizing quantities also reduces the
effects of scale that
otherwise might skew the test results.
Wood is chosen to ensure that it is of a
consistent type and moisture
content, and its calorific value and
moisture content are measured.
All other factors, including pots, lids,
and cooking equipment, are
standardized to the extent possible.
If there is to be more than one
cook, each cook should test each stove the
same number of times to
eliminate any possible bias due to
different cooking habits.
2. Test
conditions are recorded, the stove and pot(s) are described in
detail, the stoves are cleaned of ash, and
the wood is weighed and
recorded.
Pot lids are used if done so typically in the region.
If
used, they are weighed with the pot.
The food is prepared for cooking.
Food is precisely weighed out as indicated
in the sample CCT test sheet
bsex94.gif (600x600)

shown in Worksheet 2.
3. The fire
is lit and the cooking begun. The cook
does the cooking in
the usual manner and decides when the food
is done. Cooking times and
any relevant observations are recorded,
including comments by the cook
on difficulties encountered in using the
stove or other observations
such as excessive heat, smoke, or
instability.
4. The
charcoal and remaining wood are weighed and the cooked food is
weighed.
The specific consumption is calculated by:
SC =
[M.sub.w] - 1.5[M.sub.c]
--------------------------
(Total Food Cooked)
where [M.sub.w] and [M.sub.c] are as
previously defined. If desired, this
can also be
normalized to ambient temperature as for
the laboratory test.
If the wood and charcoal species, moisture
contents, and calorific
values are known, they should be reported
so as to allow standardization
of the SC.
5. The tests
are repeated at least three times or as needed to get sufficiently
precise statistics to make reliable
distinctions between the
various stoves.
The average, standard deviation, and
confidence limits are calculated
for each stove from its test results.
Stoves are then distinguished by
use of the t-test.
If a particular parameter has been varied,
linear
regression can be done between that
parameter (or its square, cube,
etc., if it has a nonlinear influence) and
the SC. Many of the other
cautions cited above for laboratory tests
are also applicable for
cooking tests and should be reviewed.
An example of
CCT data is shown in Table 2. The high
fuel economy of the
lightweight
channel type metal stove relative to both the traditional
stoves and to
these particular massive multipot stoves is quite striking.
It is also
important to note that even though the laboratory PHUs of the
multipot
stoves were significantly higher than that of the traditional
open fire,
their CCT fuel economies were only marginally better and
sometimes
worse. The reason for this is that the
additional heat recuperated
by the second
and subsequent pots increases the laboratory PHU, but
is
ineffective in actually cooking food because it is too low in temperature
and because
it cannot be easily controlled. An
analysis of the data
in Table 2 and
those for other stoves has shown that the performance of
multipot
stoves in actual cooking of food is better predicted by their
first pot PHU
than by their total PRU (5). This
strongly supports the
discussion in
Chapters III and IV concerning the poor control efficiency
of multipot
stoves.
On the basis
of the results from the laboratory and controlled cooking
tests, models
must be selected for production and field testing.
The
choice should
not be made solely on their relative fuel efficiency,
however.
Instead, it must be based on the entire
range of factors that
will
eventually determine the consumer's choice.
High cost, for example,
may be a far
more significant barrier to the rural dweller than the urban
dweller.
The smoke from a high efficiency chimneyless
stove may be far
more annoying
to the user of a stove with a chimney, though perhaps an
inefficient
one, than for the user of an open fire.
Quantifying
the subjective factors that determine stove acceptability
bsex950.gif (600x600)
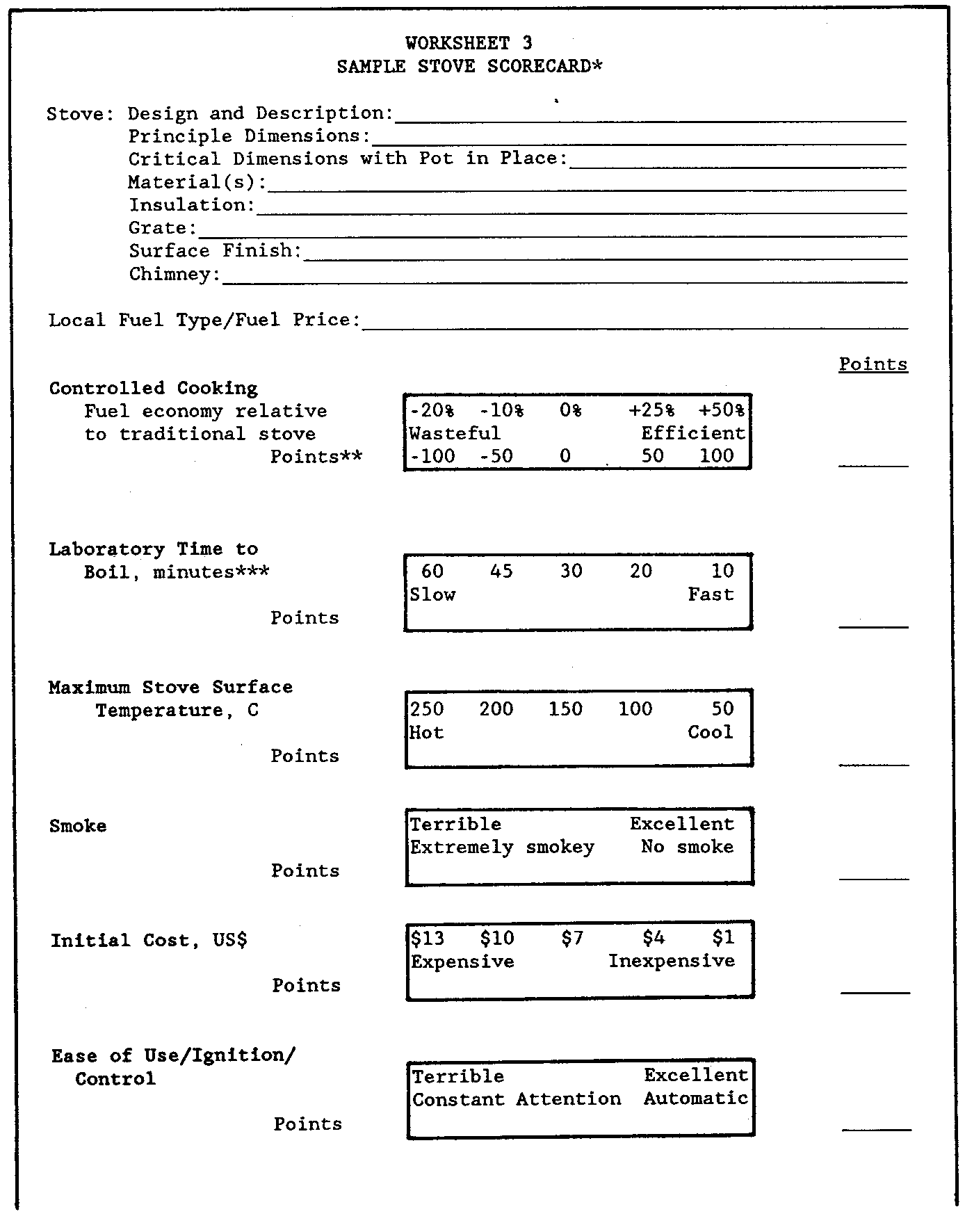
through the
use of a scorecard is difficult, but may help indicate the
acceptablity
of a stove in the field. Of greater
importance is that the
scorecard
reminds the stove developer to pay attention to more than just
fuel
efficiency.
TABLE 2
Controlled Cooking Test Results for Woodstoves
BURKINA FASO,
1983 Laboratory
Controlled Cooking
(Table 1)
Specific
PHU
PHU
# of Consumption
# of
Economy
STOVE
Pot 1
Total
tests grams wood
tests
Traditional
Stoves
Three Stone Fire
17.0 17.0
9
268[- or +]21 4
0
Massive
Multipot Stoves
Nouna 2
15.2
22.1 10
244[- or +]19
5 +9
AIDR 3
14.8
21.8 10
304[- or +]29
4 -13
Banfora
18.8
26.7 10
213[- or +]29
6 +14
Lightweight
Channel Stoves
Metallic
29.1
29.1 9
161[- or +]5
3 +40
NICER,
1983 PHU Total
(High Power)
Traditional
Stoves
Metal Malgache
21.5[- or +]1.76
6 392[- or +]129
4
0
Lightweight
Channel Stoves
Metallic
31.2[- or +]4.3
14 228[- or +]57
4
42
References:
(5,6)
PRODUCTION
TESTS
After stove
prototypes are optimized in laboratory tests and their fuel
saving
potential is verified in controlled cooking tests, the next step is
to distribute
such stoves to a large group of families in the field to
observe the
stoves' performance, acceptability, lifetime, and other
characteristics
in day-to-day use. At this point a
production test can be
run to
construct the stoves necessary for field tests as well as to
provide
valuable information as to their ease of production, production
costs,
quality control, and other factors.
A production
test is done simply by producing a large number of standard
sized stoves
as rapidly as possible while timing the various steps,
evaluating
the cost of all the inputs, observing the quality of the stoves
produced, and
determining possible ways to improve the process in terms of
cost,
quality, rapidity, or other factors. Additionally, local technical,
managerial,
and extension abilities and needs should be evaluated.
The procedure
will vary depending on the type of stove as well as the
material
used. Ceramic stoves will require
extensive material preparation,
molding on
standard forms, drying, and firing, each of which are
distinct steps
requiring separate evaluations.
Described briefly below
are the steps
used in a production test of metal channel type stoves.
1. The most
popular pot sizes and shapes are determined through surveys of
local pot makers, merchants, and
households. The pots made by different
pot producers are precisely measured to
determine if they are standardized.
If the pots vary sufficiently in size to
affect performance
significantly when used on a standard sized
stove, it may be necessary
to sell stoves designed for each specific
pot at the site of the
producer, i.e., stove-pot packages. For
example, if the comparable 0.3-m
pots of two producers differ by 8 mm in
diameter, then from
Figure III-11, the performance of a stove
designed to have a channel gap of 8
mm (by 10 cm long) with the larger pot and
a fuel savings of roughly
43% would decrease to a 20% savings with
the smaller pot. This is a
drop in expected fuel savings of over
one-half, a significant decrease.
Alternatively, a stove designed for the
smaller pot would be too tight
and not function with the larger.
2. Once
optimum stove dimensions are determined through laboratory and
controlled cooking tests, and once stove
sizes are chosen based on the
results of the pot surveys, templates are
prepared on paper and then
transferred to sheet metal to provide a
permanent copy. (To prevent the
template's loss through use itself for a
stove, metal bars can be
welded across it to prevent rolling it into
a cylinder.) An example of
template design for cylindrical or
spherical pots was given in Chapter
IV.
Dimensions there were nominal and will have to be adjusted based
on laboratory data and the pot size.
Dimensions may also have to be
adjusted to minimize material costs.
For example, the height of the
template might be adjusted to squeeze one
additional stove out of a
standard sheet of metal.
The question then is what is the loss in
performance with the lower stove wall
versus the decrease in material
costs.
Whether the lowered cost is locally perceived to be worthwhile
is often very hard to determine. In some
cases the purely psychological
advantage of, for example, keeping the
finished stove price under an
even amount, e.g., $5.00, will make the
adjustment worthwhile in terms
of increased public interest and sales.
3. When the
template has been developed, various metal shops are contacted
and commissioned to make several stoves
each. One or two shops are
chosen for the production test based on
their construction quality,
price, and other desirable factors. A
minimum of 50-100 stoves in each
of the chosen pot sizes should be ordered
from each shop. Production
is then run along the general format
indicated in Chapter IV.
4. Finally,
the production process is analyzed to determine how it might
be improved. Among the factors to be
evaluated are:
o The production rate as a function of each
step in the production line
as well as the total process and how to
optimize this rate. The
example in Table 3 shows that cutting the
stove form out of sheet
metal and then later welding it and the
pot supports into place were
by far the slowest steps in the
production process. The addition of
better or additional metal cutting and welding equipment and jigs
may
then offer an opportunity to increase
shop productivity considerably.
o The costs of production as a function of
material, labor, electricity,
rent, amortization of equipment, profit,
etc., and how to
minimize this cost.
Examples are given in Tables 4-6.
As seen in
Table 4, the
cost of metal accounts for over half the total stove
cost.
The use of lower cost alternatives such as recuperated scrap
or lighter gauge metal may therefore
offer a significant opportunity
to reduce costs. It should also be noted
that labor is a very small
component of the total costs; increasing
shop productivity by
purchasing better metal cutting and
welding equipment may then be a
less important consideration in this
case. In contrast, the very
large labor and transportation costs of
producing massive stoves on
site should be noted in Table 6.
o The quality of the finished product in
terms of respect for dimensions,
roundness, professional finish, etc., and
how to monitor and
regulate quality control.
o The possibility of introducing a
professional finish for these stoves
such as heat resistant paint,
electroplating, electropolishing, or
others to improve the stove's lifetime,
performance, and saleability.
Options might
include modifying the form of the stove away from its
thermal
performance optimum, as already discussed, in order to reduce
material
costs; simplifying the curves of the conical template in order to
maximize
production rates; or substituting recuperated metal or lighter
weight metal
to minimize the material costs and/or improve the stove's
cost/benefit,
marketability, or lifetime.
TABLE 3
Production Times for Metal Stoves,
Burkina Faso, 1983(*)
Production Step
Time (minutes)
for 8 stoves
1.
Tracing stove from template
10
2.
Cutting stove
49
3.
Bending/hammering into cylinder
15
4.
Cutting pot clamps and pot supports
18
5.
Cutting and/or punching grate
12
6.
Bending the air holes
14
7.
Welding
64
8.
Painting
30
TOTAL
212 minutes
Per Stove
26.5 minutes
(*) The
design was a single wall, chimneyless channel type stove as described
in Chapter
IV; Template Design: Cylindrical Stoves and Metal
Stove
Production.
References
(11,12). See also reference (6) for similar data from Niger
TABLE 4
Lightweight Metal Stove(*) Production
Costs, Burkina Faso, 1983
Material costs per stove
US$
metal sheet
1.41
pot supports and clamps
0.24
grate
0.19
welding
0.08
paint
0.11
Subtotal
2.03
Labor costs per stove
(four employees)
0.14
Operating costs per stove
rent of hut
0.03
electricity
0.02
transport to market
0.03
Subtotal
0.08
Total Production Costs
2.25
profit: owner
0.37
profit: project
0.13
Sale price by project
2.65
(*) The
design is as described in Table 3.
References
(11,12). See also reference (6) for similar data from Niger
TABLE 5
Lightweight Fired Clay Stove(*)
Production Costs
Burkina Faso,
1983
US$
Labor costs per stove(**)
0.13
Firing
0.06
Metal grate
0.25
Transport to market
0.13
Total production costs
0.57
Profit
0.93
Sale price
1.50
(*) The
design was a single wall, chimneyless channel type stove as
described in
Chapter IV; Fired Clay Stove Production.
(**) Material
costs per stove are included under labor for digging clay.
Reference
(13)
TABLE 6
Massive Multipot Stove
Production Costs
Burkina Faso,
1983
Material costs per stove
US$
Bricks
1.20
Cement
2.88
Chimney
1.01
Sand and gravel
0.63
Subtotal
5.72
Labor costs per stove
8.86
Transport costs to site
7.92
Total production costs
22.50
Subsidy by project
11.25
Sale price by project
11.25
(*) 400 CFA - US$ 1
References (11, 12)
FIELD TESTS
Field tests,
or kitchen performance tests, of improved stoves are critical
to
determining how well stoves perform in actual use and how acceptable
they are to
local cooks. In designing the tests and
choosing participants,
it is
important to consider a wide range of socioeconomic data and
other factors
(14-16). A particularly useful review
of rural energy
surveys and
techniques is given in (14) and additional information is
given in
(15,16). Examples of sociological
surveys are given in (17,18).
In recent
years greater attention has been focused on the interconnections
between
energy use in households, smallholder agriculture and farm
animals, and
informal commerce and industry, among others.
Such surveys
are proving
crucial to the understanding of the dynamics of rural economies;
relevant
studies are cited in Note (24).
Researchers
examining hazardous smoke emissions from stoves may want to
include
medical questions such as the incidence of eye and lung disease,
i.e., eye
irritation, coughing, etc. Relevant
information can be obtained
from the
East-West Center (Appendix J).
While a
detailed review of survey techniques as applied to traditional
energy in
developing countries is far beyond the scope of the presentation
here, there
are a number of useful questions that should be asked.
Some
of these are
listed below:
o
Who cuts the
wood and how? Who produces
charcoal and how? What are
the labor and transport techniques and
costs for these fuels? Are fuels
carried only in backhaul that would
otherwise be empty cargo space? Is
this activity the domain of a particular
ethnic group, economic class,
sex, or age?
Are these activities considered socially demeaning?
Is
it a social activity?
Do children collect fuel? -- and does this
encourage larger families or deprive
children of their education? Is
the use of dung considered socially
demeaning?
How do all these factors change with the
shift from subsistence
foraging to commercial production and
marketing?
o
What fuels are used and at what time during
the year -- crop residues
following harvest, dung, wood, etc.?
What are the competing uses for
the fuels -- fuel, fodder, fertilizer,
construction-material, artisanal
uses, industrial heating, domestic
heating? Are the higher quality
fuels sold to urban areas leaving lower
quality fuels for rural use?
Is wood green or thoroughly air dried
before use?
o
Where is the fuel taken from? Who owns the
land -- government, wealthy
absentee landlord, peasant, community?
Who gathers the fuel from this
land?
Are permits required? How are
they obtained? What are the
competing uses for that land -- trees or
fuel crops, food crops,
fodder?
Are trees killed when fuel is taken or are only branches
pruned? Are trees replaced?
o
What is the history of the region -- the
trends in its population
density and distribution, farming
techniques and intensity, forest
density, building of roads, development of
commercial timber harvesting,
etc.?
What is the nature of the local community -- its size,
sources of income, growth rate?
In performing
surveys a few potential biases must be kept in mind as well.
These
include:
o
Cultural perceptions of time, distances, and
other factors can vary
dramatically. Direct observation is needed.
o
Field research should include all seasons --
not just the dry season,
nor just the "academic" season.
o
Respondents often exaggerate their personal
situation or say what they
think the interviewer wants to hear.
To avoid this, questions should
focus on specific past actions, for
example, "Have you ever used a type
X woodstove?."
Alternatively, questions might be posed in a
negative
or leading manner to offset a respondent's
tendency to answer affirmatively.
Whether or not this is useful will depend
strongly on the
local culture.
Negative or leading questions must be used with great
care to prevent them from introducing a
bias in their own right.
o
Some questions should be left open-ended so
that the respondent can
provide some direction or provide types of
information not initially
anticipated.
Otherwise the results will tend to reflect the preconceived
notions of the person writing the
questionnaire. As an example,
one could ask an open-ended question such
as "what did your household
like (dislike) about the stove?"
o
People near rural roads, the most frequently
visited, tend to be
wealthier, more experienced, and more
integrated into the market
economy than those with less access to
roads.
o
Key informants are unusual people and often
do not represent the norm.
o
People reporting on social behavior often
cite the ideal and not the
norm. Their comments are useful but must be
independently checked.
Given these
general questions and considerations, the following are
specific
proposals for determining the acceptability and performance of
improved
stoves. Countless variations of these
are possible and should be
developed in
order to respond well to local conditions.
For any survey
method,
however, a preliminary test should be run to determine if it is an
effective
approach before beginning a full-scale effort.
The families
involved should not, under most conditions, be given the
stove free of
charge on a permanent basis as this will bias potential
buyers to
wait for the next giveaway. Instead,
for the acceptability and
wood
consumption surveys, the stoves can be distributed on a trial basis,
at the end of
which either the user buys the stove at a slightly reduced
rate
consonant with the degree to which they were disrupted during the
survey, or
they return the stove and are in turn themselves paid for their
trouble in
assisting during the survey. This also
indicates somewhat the
value they
place on the improved stoves. For
families that do not buy the
stove there
should be a follow-up a few days later to observe how they are
adapting to
the traditional stove.
Finally, when
conducting surveys generally, it is important to be highly
suspicious of
any and all data. Frequent, independent
verification of
results by
varying the questions and the survey technique is an important
component of
a field program.
Acceptability
Surveys
Acceptability
surveys normally consist of:
o
A background sociological, economic, and
cultural survey with questions
bsexws70.gif (600x600)

such as those indicated in Worksheets 4, 5,
and 7.
o
Distribution of stoves (produced in a
production test) on a trial basis
to perhaps 100 families for a three- to
six-month period, or longer;
o
Visits every week or two to determine the
condition and status of the
stoves and what difficulties users of the
stoves have. Typical
bsexws50.gif (600x600)

questions are given in Worksheets 5 and
7. It is particularly important
to note whether or not the stove is in fact
used. For this,
visits at mealtimes are useful; the stove
can be inspected to see if it
is warm or not, or if the ashes are fresh
or not. If still in doubt, a
piece of straw or other material can be
covertly placed in the stove to
indicate later whether or not the stove was
used during the interim.
Additionally, it is important to estimate
the lifetime of the stoves by
monitoring their condition over a long
period.
o
A final questionnaire, like those in
Worksheets 5 and 7, to determine
the general user response to the stove and
why. With care, the
questions may be posed in a leading or
negative manner as necessary.
Wood Economy
Surveys
Wood economy
surveys normally consist of all the components of an acceptability
survey and,
additionally, include regular (i.e., daily) weighing
of the fuel
used by a family to determine fuel consumption using both
traditional
and improved stoves. The financial impacts, among others, on
a family
using an improved stove can also be determined.
Typically, a
wood economy
survey will require monitoring the fuel use of at least 40
families or
as needed to generate statistically significant results.
Because wood
economy surveys attempt to be quantitative, they are much
more
complicated than acceptability surveys.
A number of errors are
possible that
reduce the usefulness of the data.
Typical errors include
the
following: The loss of fuelwood by loaning or trading it to neighbors
or carrying
it off elsewhere for other uses (such unexpected and diverse
uses could
include hitting goats to drive them out of the garden).
The
addition of
unweighed fuel to the kitchen pile. The
family giving the
same response
each day regardless of the real situation (for example
saying the
number of people eating at a meal is the same when it is known
to
vary). The seasons changing during the
course of testing (e.g., the
winter
heating season or the rainy season beginning or ending), or
religious
holidays taking place. The family being
wealthy and not
worrying
about reducing wood consumption or the families compared being
from markedly
different economic levels. Simply the act of weighing the
wood daily
may sensitize the user and tend to cause the amount used to
decrease
(19). In addition, in many cases the
family will not use the
improved
stove part or all of the time, giving a wood economy that is a
corresponding
fraction of the true potential of the stove.
Several
different approaches are possible that reduce these problems.
For
all surveys
generally, an attempt is made to test the same family with
both the
traditional and the improved stove, to instruct families carefully
on the
importance of using weighed wood for cooking only and to
cook only
with weighed wood. Additionally,
families are chosen that are
reasonably
homogeneous in economic level, size, living situation, etc.
Beyond that
are the following options, among others:
o
The tester can remain with the same family
for the entire day observing
all fuel uses and manners of use.
The stove tested can be varied as
desired.
Such rigid control eliminates many of the problems listed
above, but is an exceedingly tedious method
of gathering very few data.
Such an effort is recommended once or twice
in any survey, but is too
expensive and time consuming for
large-scale surveys.
o
For the same family, the tester can weigh
fuel on a meal by meal basis.
In some regions where fuel is gathered
before every meal, this is
unavoidable.
This is somewhat less tedious than the method above and
it still allows reasonably good control
over both fuel and stove use.
The stove tested can be varied as desired.
Stoves can be switched
(i.e., traditional stove to improved stove
and back) on a weekly or a
daily basis.
Frequent switching of stoves (i.e., daily, or even meal
by meal [20]), however, can seriously
disrupt a household. In areas
where extra food is prepared for guests who
may come later, data from
daily or meal by meal switching of stoves
can also be skewed by the
amount of leftovers.
Finally, with any stove there is a certain
natural learning time before the optimum
use is achieved. Switching
stoves too frequently will tend to reduce
use below optimum.
o
The stoves can be switched back and forth
with the same family on a
weekly basis.
A few days to a week are provided between weighings to
give the user time to readjust to each type
of stove. This procedure
is listed in Table 7.
Of these
methods, switching stoves back and forth with the same family on
a weekly
basis is preferred. Such a procedure is
particularly valuable
because it
eliminates potential biases created by comparing different
families.
Additionally, it compensates for the
automatic reductions in
consumption
regardless of stove as the stove user becomes sensitized to
daily wood
use by the act of daily weighing. The
major difficulty is
ensuring that
a particular stove and only that stove is used during its
proper week.
If there is
difficulty in getting a family to switch back and forth
between
stoves, other families can serve as a control group for those
receiving the
improved stove. These data can then be used to subtract the
effect of the
act of measuring itself on fuel consumption or the effects
of seasonal
change, etc. In this case the procedure
might be as shown in
Table 8.
Whatever the
precise methodology chosen, the steps in the process are then
to:
o
Interview the families who may participate
to obtain background data as
bsexws40.gif (600x600)

shown in Worksheet 4.
Families should be chosen in order to be as
homogenous as possible -- similar income
level, family size, etc.
o
Weigh the wood in participating households
on a daily basis as in
bsexws6.gif (600x600)

Worksheet 6.
The tester should arrive at roughly the same time each
morning at a particular house, weigh the
amount of fuel left from the
day before, and weigh the amount of fuel to
be added to the kitchen
pile for that day. It is helpful if the
"kitchen" pile is no more than
twice the daily fuel consumption.
The fuel in the kitchen pile must
not be used for any purpose other than
cooking in that kitchen with the
stove being evaluated.
If it is used with a variety of stoves, then
the final numbers will be some average of
the performance of the
various stoves used.
The number of people eating at each meal the
previous day is determined and from this
the number of adult equivalents
is calculated using Worksheet 6. Other
questions can be asked as
desired as indicated at the end of
Worksheet 6.
o
Follow (daily fuel use) data collection with
summary questionnaires as
bsexws50.gif (600x600)

illustrated in Worksheet 5.
Results should be shared with each family
at the end of the testing and families
should be thanked. Final disposition
of the stoves -- sold at a reduced price to
the family or
returned -- should be done and tabulated.
A number of
sample biomass stove survey forms and questions are included
below.
In many cases it may also be useful to
conduct surveys of the
fuelwood and
charcoal producers and sellers as discussed in reference
(21).
Before beginning a full-scale survey, each
question and each survey
form should
be pretested to ensure that it is useful for that region, and
that it gives
reliable responses. If desired,
questionnaires can be
numbered for
computer tabulation (this will not be worthwhile except in
the largest
of studies).
TABLE 7
Preferred
Methodology
Alternating Stoves Used By
Each Family Weekly
Time
Activity/Stove
Week
1 Daily wood weighings
with stove A
Week
2 No wood weighings,
learning to use stove B
Week
3 Daily wood weighings
with stove B
Week
4 No wood weighings,
relearning to use stove A
Week
5 Daily wood weighings
with stove A
Week
6 No wood weighings,
relearning to use stove B
Week
7 Daily wood weighings
with stove B
Etc., as desired
TABLE 8
Using Control Groups While
Alternating Stoves
Time
Period
Group A
Group B
(Control Group for A)
Week 1:
Daily wood
weighing. On the stove currently
On the stove currently
used by the
family. used by the family.
Week 2:
Sensitizing
the Provide the family
Family continues to
family on the
need with the new stove
use current stove.
to reduce
wood use to be evaluated;
and how to do
it; teach them how to
no daily
weighings. use it.
Week 3:
Daily wood
weighing. On new stove.
On current stove.
Week 4:
Sensitizing
as in No further work
Provide the family
week 2
with this family.
with the new stove;
teach them how to
use it.
Week 5:
Daily wood
weighing - - - -
On new stove.
MARKETING
TESTS
Marketing
tests follow the successful completion of field tests.
A major
component of
marketing is promotion and among promotional possibilities
are radio and
newspaper advertising, billboards, printed fabrics and
buttons,
songs and sound trucks; public demonstrations at social centers,
schools,
religious centers, and other public places; and stove sales by
commission at
various commercial outlets. A
particularly effective
technique for
public demonstrations is to provide enough wood to complete
the cooking
when using the improved stove but not enough when using the
traditional
stove. When public demonstrations are made it is important to
have stocks
of improved stoves available for immediate sale; otherwise
potential
customers can become frustrated. In
areas with relatively small
markets and a
well-established traditional stove, rapid marketing can be
done by
commissioning all traditional stove producers and commercial
outlets to
make and sell only the improved version during a trial period.
Much of the
focus of any marketing effort must be to train users how to
select the
best stove for their purpose. Such
factors as recognizing the
importance of
the channel gap and how wide it should be are crucial.
Additionally,
it may be necessary to provide independent quality control
of stove
production, providing an easily and (by educating the user)
widely
recognizable stamp of certification or warranty for stoves that
meet the
requirements.
Users must
similarly be taught how to use the stove correctly.
This was
discussed in
Chapter III under Control Efficiency.
Failure to train users
how to
minimize fuel consumption can greatly reduce the potential savings
of any stove.
Initial
marketing efforts are best directed at urban areas where there is
already a
cash economy and where fuel costs are highest.
Once an urban
stove market
is established, the stove may then spread more easily to
rural areas,
driven in part by the prestige of being a modern (urban)
stove.
The general problem of stove dissemination
in rural areas is,
however, a
particularly difficult one (25) and much additional study is
needed.
Marketing
efforts should also attempt, to the extent possible, to use
existing
avenues to disseminate the improved stove.
Traditional metal
artisans or
potters should be included at every step of the design and
development
effort. Market vendors should be used
to sell the improved
stove.
Finally, existing neighborhood organizations
should be included in
the
dissemination effort, particularly for user training.
In all of these
cases, as
much responsibility as possible should be given to individuals
to promote
stoves in their area.
Studies
should be done of the stoves' cost/benefit ratio based on production
and field
tests and the local fuel costs.
Marketing efforts may
point out the
need for changes in the form of the stove such as putting a
professional
finish (electropolishing, electroplating, heat resistant
paint) on the
stove to increase consumer appeal, or reducing the cost
through use
of lighter components even at the expense of decreased stove
life. Different
approaches can be tried in different areas such as using
social
centers for sales in one area, commercal outlets in another, and
the results
compared. In all these cases, a record
should be kept of the
date, client,
address, family income, stove cost, stove size, etc. , so
that followup
can be done later and to provide an understanding of the
dynamics of
selling the stoves. For example, sales
at social centers
might prove
to be to women who require an emphasis on speed and ease of
use, while
sales at commercial outlets may be more frequently to men who
are more
concerned about the potential financial savings.
Finally, the
reader is once again urged to examine closely and use
regularly the
financial and statistical techniques presented in Appendixes
F and G for
the analysis of stove testing data.
CHAPTER VI
CHARCOAL
FUELED SYSTEMS
In this
chapter, the design and testing of fuel efficient charcoal stoves
and foundries
are discussed in general terms. No
prototypes are presented,
only guidelines
for their development. Charcoal stoves
have been
the focus of
intense research, development, and dissemination efforts in
Kenya (1-5)
and Thailand (6-8). Detailed
performance and production data
for Kenya,
including breakdowns of manufacturing costs, are given in (3).
In Kenya,
sales of improved charcoal stoves have grown rapidly and are far
above the
original project goals. By mid-1985,
nearly 100,000 improved
charcoal
stoves had been disseminated (3). Those
who are considering
working on
charcoal stoves are strongly urged to contact KREDP or KENGO,
ITDG, E/DI,
or the Thai group (6) (Appendix J) for design, testing, and
dissemination
data.
CHARCOAL
STOVES
Design
Considerations
Charcoal
stoves should be lightweight to minimize their absorption and
storage of
heat. Designs that thermally isolate
tbe combustion chamber
from the rest
of the stove may further reduce this stored heat.
Convective
heat transfer can be optimized in charcoal stoves by fitting
the stove to
the pot with an optimized pot to wall channel gap through
which the hot
gases must flow. The higher average
combustion temperatures,
however,
reduce the relative importance of convective compared to
radiative
heat transfer. Further, in Kenya
channel designs have met
consumer
resistance and most development and dissemination work has
focused on
insulating the combustion chamber with durable fired clay or
cement/vermiculite
linings (4).
Radiative
heat transfer is much more important in charcoal stoves than in
wood stoves
due to the higher combustion temperatures.
Further, burning
the volatiles
given off by wood requires a large combustion volume.
In
contrast,
because there are few volatiles in charcoal, radiative transfer
can be
maximized by setting the pot as close to the fire as possible with
little
concern about interfering with the combustion of volatiles.
Charcoal
beds, however, have one complication not found when burning wood.
Wood
volatiles burn above the fuel bed and the wood thus tends to burn
from the top
down. Radiative transfer is then
directly from the flames to
the pot. In
contrast, the charcoal fuel bed tends to burn from the bottom
and center
upwards, as this is the area with greatest oxygen flow and is
the best
insulated from the outside world, achieving the highest temperatures
for
combustion. Burning charcoal thus tends
to radiate heat away
from the pot
toward the stove bottom, and the charcoal next to the pot
tends to
insulate the pot from both radiative and convective heat transfer.
bse1x117.gif (600x600)

This is
illustrated in Figure 1.
To reduce
this effect and to allow the hot gas to flow freely along the
pot bottom,
it may help to support the pot slightly (2-3 cm) above the
f ire
bed. An insulated grate, insulated
combustion chamber wall, and
insulated
stove bottom or radiation shield may help reduce radiation loss
toward the
bottom and sides of the stove.
Insulating linings have been
generally
well received in Kenya (4). Fired clay
grates in particular,
however, tend
to crack in just 2-3 months. And
because of their insulating
ability it is
more difficult to light the charcoal by burning paper
or straw
below the grate (4).
Finally,
additional controls are needed despite the fact that burning
charcoal
tends to self regulate its rate of combustion by forming a layer
of ash that
slows the flow of oxygen to its burning interface.
A tightly
fitting door
to regulate the flow of oxygen into the stove is desirable.
Contrast this
with wood stoves where the firepower is best controlled by
removing the
wood and extinguishing it directly.
Each of these
factors will need to be carefully tested when developing a
practical
charcoal stove.
Laboratory
Testing Procedure
A number of
slightly different lab testing methodologies have been
proposed for
testing charcoal stoves of which several are reviewed in (9).
The testing
procedure described below is almost identical to that for
woodburning
stoves in Chapter V. The two primary
differences are that the
initial
quantity of charcoal must be standardized and that lids are used
to better define
the low power capability of the stove (10).
Controlled
cooking and
field testing procedures are the same as for wood stoves.
1. Test
conditions are recorded and the stove and pot are described in
detail.
The stove and pot are thoroughly cleaned and dried.
The
bsexws10.gif (600x600)

testing area should be well protected from
the wind. <see worksheet 1>
2. A standard
amount of charcoal, for example 0.500 kg, is weighed out for
each test.
The moisture content and calorific value should be known and
sufficient charcoal for the entire series
of tests should be available,
all of the same type, and stored in the
same place so as to have a
uniform moisture content.
If possible, the stove is weighed when empty
and then with the charcoal.
This will prevent the loss of charcoal
that could occur when transferring from the
stove to the balance pan.
This also reduces the disruption of the
fire.
It is important that the initial mass of
charcoal be the same for each
test in every stove.
Tests have shown that the calorific value of
charcoal increases as it is burned in a
stove - - probably due to the
removal of low energy volatiles (9).
3. The pot,
lid, and thermometer are weighed, and then a fixed amount of
water is added, roughly equal to two-thirds
the pot capacity but
exactly the same for each test and all the
stoves, (i.e., 5.000 kg).
The lids should close snugly and the
thermometers should sit well
immersed in the water.
4. A measured
amount of kerosene (i.e. 15 ml) is added to the charcoal,
the fire is lit, and the pot put in place
the moment that the kerosene
itself goes out.
A delay in placing the pot on the stove to allow the
fire to establish itself better can cause a
large and varying amount of
charcoal to burn during this period,
increasing the scatter of the
data.
Timing begins when the pot is put on the stove.
The fire is
fanned as needed.
The door is left open throughout the high power
phase.
5. The
temperature of the water and any actions to control the fire are
recorded every five minutes.
6. The moment
that the pot comes to a vigorous boil, the pot with lid and
thermometer and the stove with the charcoal
are each weighed and their
weights recorded.
If the balance capacity is insufficient to weigh the
stove with the charcoal, the charcoal must
be removed and weighed
alone.
This, however, is more difficult and also disrupts the fire.
7. As quickly
as possible the pot is put back on the stove, the door is
closed for the low power phase, and
temperatures are again recorded
every five minutes.
If the temperature drops more than
5[degrees]C below
the boiling point, the coals should be
stirred to improve their burning
and/or the door should be opened a crack to
increase air flow.
8. After
thirty minutes the stove and charcoal, and the pot and water are
again weighed and the values recorded.
In analyzing
the data, three parameters are calculated for each phase:
the firepower
P, the percent heat utilized PHU, and the specific consumption
SC.
The firepower
is given by:
[M.sub.c][C.sub.c]
P = -------------------- (kilowatts)
6OI
where
[C.sub.c] is the calorific value of the charcoal in kJ/kg, [M.sub.c] is the
amount
of charcoal
consumed during that phase of the test in kg, and I is the
elapsed time
in minutes. Again, it should be noted as in point 2 of the
procedure
above, that the calorific value of charcoal increases upon
burning.
This often causes serious discrepancies, for
example, between
the high
power and low power phases of the test.
In this case, the low
power phase
has a calculated PHU that is unreasonably high.
The percent
heat utilized PHU is calculated by:
4.186[W.sub.1]([T.sub.f]-[T.sub.i]) +
2260([W.sub.i]-[W.sub.f])
PHU =
--------------------------------------------------------------- x (100%)
[M.sub.c]
[C.sub.c]
where
[W.sub.i] and [W.sub.f] are the masses of the water at the beginning and end of
that phase in
kg, ([T.sub.f] - [T.sub.i]) is the temperature change of the water during
that phase in
[degrees]C. The constant 4.186 kJ/kg is the specific heat of water
and the
constant 2260 kJ/kg is its latent heat of vaporization.
The specific
consumption is given by (11):
[M.sub.c]
SC = ---------
[W.sub.f]
where
[M.sub.c] and [W.sub.f] are the same as above.
For convenience, the specific
consumption
defined here can be expressed in terms of grams of charcoal
consumed per
kilogram of water "cooked."
Alternatively,
a specific consumption that does not penalize the stove for
evaporating
water can be used. Its definition uses
instead the initial
water
quantity:
[M.sub.c]
[SC.sub.2] = ---------
[W.sub.i]
Finally, if
there is a large variation in starting water temperatures from
day to day,
the water temperature can be normalized, giving an SCN, as
done in
Chapter V.
The best
measure for the stove's performance, PHU, SC, or [SC.sub.2], must be
determined by
comparing laboratory data to controlled cooking and field
testing
data. At present, such data are not
generally available.
Design
Parameters To Be Tested
A number of
different parameters affecting stove performance should be
examined.
Among these are the following.
o
pot to wall channel gap;
o
pot to wall channel length;
o
use and placement of insulation;
o
use of an insulated stove bottom or
radiation shield below the grate;
o
hole density of the grate;
o
mass of the grate and the possible thermal
isolation of the grate from
the rest of the stove;
o
use of low cost bellows to achieve high fire
powers quickly;
o
grate-to-pot height (leaving a small space
for free airflow between the
charcoal and the pot);
o
form of the grate -- conical, flat, etc.;
and
o
injection of secondary air to reduce of
carbon monoxide. Tests of a
west african charcoal stove have shown that
secondary air could reduce
CO emissions by 25% (11).
Sample Data
Tables 1-5
summarize test data from (9) and are presented here as examples
of the type
of data that are generated by the charcoal testing procedure.
These data
are particularly useful in demonstrating differences between
wood and
charcoal stoves. Additionally, these
data illustrate aspects of
both test
methodology and data analysis that may mislead the unwary.
Four tests
were done for each combination of channel gap, length, and the
use of
insulation. The coefficient of
variation (Appendix G) was typically
0.1 or
less. Several comments can be made
about these data:
o
There is a dramatic increase in the PHU
between the high and low power
phases.
This is due to both thermal inertia and a varying calorific
value of the charcoal in the stove.
The energy needed to warm the
stove during the initial high power phase
(the stove is cold at the
start) will lower the PHU compared to the
later, low power phase.
Further, the charcoal burns its lower
energy volatiles at the start of
the test.
Using an average calorific value will then cause the
calculated PHU to be overstated during the
high power phase and
understated during the low power phase.
o
The observed PHU during the high power phase
is independent of the
channel gap and length and the use of
insulation. This suggests that
the dominant factor here is the thermal
inertia of the stove.
o
Large increases in PHU occur during the low
power phase with the use of
insulation and longer and narrower
channels. This is expected from
consideration of conductive and convective
heat transfer processes. A
multiple linear regression on this data is
presented in Appendix G.
These efficiency increases, however, have
little effect on the overall
PHU because little energy is used during
the second phase.
o
The total PHU increases weakly with
increasing channel gap, channel
length, and use of insulation.
The rather odd result that a wider
channel gap should give a higher PHU is in
fact due to that stove
burning a large amount of charcoal during
the second phase and thus
more heavily weighting that higher
efficiency phase in the total. In
other words, the stove with the wide
channel gap burned too much fuel,
but the PHU showed this not as a loss, but
as a gain. The PHU is,
then, a poor indicator of the fuel
efficiency of a charcoal stove.
o
The specific consumption shows no effect for
varying channel length or
insulation; only the channel gap reduces
consumption, and the 3-mm gap
has a significant savings over the stoves
with 5- or 8-mm gaps or the
traditional malgache stove.
o
The SC shows little change over [SC.sub.2]
for the 3-mm gap but a significant
increase in consumption for the 5-mm and
8-mm gaps. This indicates, as
did the PHU, that, for whatever reason, the
control of air flow through
these latter stoves is much less efficient
than for the 3-mm stove.
That is, the larger channel gap results in
much greater firepowers and
excess evaporation.
This also indicates that SC is a more
sensitive
measure of stove performance than
[SC.sub.2]. The importance of air
supply on
the high and low power performance of
charcoal stoves has also been
noted in (12) with regard to testing of the
Umeme stove.
TABLE 1
Charcoal Stove(*) Tests,
Senegal 1983-84
High Power Phase:
Summary of PHUs
Channel
Length
No Insulation
With Insulation
Channel
5 cm 10 cm
15 cm
5 cm 10 cm
15 cm
Gap
3 mm
25.9 27.0
26.0
26.0
26.2 26.9
5 mm
25.0 23.8
25.7
24.2
25.2 24.5
8 mm
24.7
25.1
25.1 25.9
24.9
25.6
Traditional West African
"Malgache" Stove: 23.0
TABLE 2
Charcoal Stove(*) Tests,
Senegal 1983-84
Low Power Phase: Summary
of PHUs
Channel
Length
No Insulation
With Insulation
Channel
5 cm 10 cm
15 cm
5 cm 10
cm 15 cm
Gap
3 mm
41.4 36.5
62.2
57.5
68.6 78.4
5 mm
36.9 43.9
47.7
50.2
71.9 77.3
8 mm
39.1 46.1
54.3
48.8
61.7 64.9
Traditional West African
"Malgache" Stove: 24.0
TABLE 3
Charcoal Stove(*) Tests,
Senegal 1983-84
Both Phases: Summary of
PHUs
Channel Length
No Insulation
With Insulation
Channel
5 cm 10 cm
15 cm
5 cm 10 cm
15 cm
Gap
3 mm
27.4
28.0 29.0
28.8
30.3 31.3
5 mm
27.3
26.7 28.9
29.5
32.6 31.9
8
mm 28.1
29.9
32.6 31.3
33.3
35.5
Traditional West African
"Malgache" Stove: 23.4
TABLE 4
Charcoal Stove(*) Tests,
Senegal 1983-84
Summary of Specific
Consumption SC(**)
Channel
Length
No Insulation
With Insulation
Channel
5 cm 10 cm
15 cm
5 cm 10 cm
15 cm
Gap
3 mm
66.7
65.0
65.4 66.0
66.0
65.1
5 mm
79.0 76.7
72.6
84.5 76.6
77.0
8 mm
85.2 86.9
89.3
82.8 88.1
89.5
Traditional West African
"Malgache" Stove: 95.8
TABLE 5
Charcoal Stove(*) Tests,
Senegal 1983-84
Summary of Specific
Consumption [SC.sub.2](**)
Channel
Length
No Insulation
With Insulation
Channel
5 cm 10 cm
15 cm
5 cm 10 cm
15 cm
Gap
3 mm
64.7 63.2
63.0
63.7 63.1
62.1
5 mm
74.5 72.8
68.7
77.8 70.3
71.2
8
mm 79.0
79.3 79.8
75.7
78.4 78.2
Traditional
West African "Malgache" Stove: 23.0
(*)Tests are
based on a conical type charcoal stove with a constant pot-to-wall
channel gap;
an operable door; a grate with a 30% hole density; and a
pot-to-grate
distance of approximately 5 cm.
(**)Calculations presented
here are
normalized with respect to initial water temperatures (13).
These results
contrast sharply with the case for woodstoves.
The PHU for
woodstoves
was found to be a reliable indicator of their cooking performance
in tests in
West Africa (14). Further, tests there
found the
performance
of channel type woodstoves to be highly dependent on the
channel
dimensions and the use of insulation, as discussed in Chapter III
(15).
These differences between charcoal stove and
woodstove performance
are due
primarily to differences in the combustion characteristics of
these
fuels. In particular, heat transfer in
charcoal stoves is due
primarily to
radiation; convection is predominant in woodstoves.
Control
of a charcoal
stove is a function of the airtightness of the door and
other factors
within the stove itself, while woodstoves are controlled
simply by
removing the wood.
HIGH
TEMPERATURE FURNACES
A large
amount of charcoal is used by artisans in fabricating metal
objects such
as aluminum pots. In the region of San,
Mali, for example,
preliminary
estimates by the Mali Solar Energy Laboratory (16) are 155,000
kg of wood
used for cooking and other purposes and 31,000 kg of charcoal
used for
blacksmithing work each year. If the
conversion efficiency of
wood to
charcoal is assumed to be 20%, then 155,000 kilograms of wood were
used to
produce this charcoal.
Traditional
forges are flexible and easy to make and maintain but they are
inefficient.
By shielding against radiant heat loss and
by using counterflow
heat
exchangers to recuperate waste heat, such forges could be made
much more
efficient.
A typical
traditional foundry for aluminum pot production consists of a
metal barrel
sunk into the ground for insulation and lined on the inside
bse2x126.gif (480x480)

with a banco
mixture to protect the metal from corrosion (Figure 2).
Leaving a
space below for the plenum chamber (air entry and ash collection),
heavy iron
rebar is laid horizontally to act as a grate.
The top
of an old
barrel is laid over the entire system to reduce radiant heat
losses.
The forge is activated by a small hand
driven blower forcing air
through a
5-cm-diameter pipe into the plenum chamber below the grate and
then into the
charcoal bed.
The use of an
air-to-air heat exchanger design may significantly improve
the
efficiency of these foundries. An
example design consists of two
bse3x126.gif (540x540)

dependent
parts (Figure 3): a tightly fitting insulated lid to reduce
radiant heat
loss and to seal the top of the furnace from air leaks, thus
forcing the
hot gases to go through the heat exchanger; and a counterflow
heat
exchanger to recuperate waste heat by capturing it in the incoming
combustion
air. The lid can be made of metal and
whatever high temperature
insulation is
available. However, the lid and the top
of the heat
exchanger
must be carefully matched so that they seal and prevent the
combustion
gases leaving the furnace from bypassing the heat exchanger.
Banco could
be used to improve the matching of the cover and the top of
the heat
exchanger in sealing. Additionally,
allowance must be made for
thermal
expansion of the metal, parts and easy access to the interior so
that fouling
residues can be removed. Details of the
mathematical analysis
bse4x127.gif (600x600)

are given in
Appendix E and results are shown in Figure 4.
As an example,
a 2-m long
heat exchanger with an 8-mm gap can potentially recuperate 68%
of the energy
of the fire, or 6.8 KW in this case, at the cost of 3.7 W in
additional
effort needed to operate the fan. That
is a return of nearly
2000 to 1.
Such heat
exchangers may also be useful in improving the efficiency of
ovens, crop
dryers, and other such devices. For
example, the use of heat
exchangers in
tobacco curing sheds in Malawi reduced fuel use by 27% and
drying time
by 20% (17). Additional references on
the technical aspects
of heat
exchanger design and development are listed in Appendix E.
APPENDIX A:
CONDUCTION
For heat
conduction in isotropic materials, assuming no heat generation
bsexeq1.gif (101x528)

within the
material itself, the differential equation is: <see equation 1>
where T is
the interior temperature distribution, t is the time, and
[alpha]=k/[[rho]c.sub.p]
is called the thermal diffusivity where k is the
thermal
conductivity, [rho] is the density, and [c.sub.p] is the specific
heat (1,2).
The operator
[Laplacian operator] is given in various coordinate systems
by: <see
equations below>
bsexeq2.gif (200x600)

Heat Flow
Through An Infinite Slab
Consider an
infinite (in y and z directions) slab with thickness s in the
x direction
and temperatures [T.sub.1] and [T.sub.2] on its two faces.
In the steady
state the
heat conduction equation for this system becomes <see equation 5>
bsexeq5.gif (84x600)

bsexeq6.gif (60x600)

This has
solutions of the form <see equation 6>
Applying the
boundary conditions <see equations below>
bsexeq7.gif (145x600)

The Fourier
conduction law gives <see figure 9> <see figure 1 to 4>
bsexeq9.gif (84x600)

bsex130.gif (600x600)

where n is
the surface normal. Thus, in this case <see equation 10>
bsexeq10.gif (75x600)

where (s/ka)
is a thermal resistance.
Now consider
the case of an infinite slab with a hot gas on one side and a
cold gas on
the other.
Beginning
again with <see equation 5>
bsexeq5a.gif (94x600)

there are
solutions of the form <see equation 6>
bsexeq6a.gif (84x600)

Now the
boundary conditions for convective heat transfer, discussed in
Appendix B,
are applied: <see equation 11>
bsexeq11.gif (84x600)

where
[h.sub.1] and [h.sub.2] are the surface convective heat loss coefficients
(Appendix
B) and the
equations are to be evaluated at x=0 and x=s, as indicated.
The
difference in sign between the two surfaces is determined by whether
heat flow is
in the direction of or opposite to the surface normal.
Applying
(dT/dx)=a from equation (6) and evaluating T-ax+b at x=0, x=s <see equation
12 and 13>
bsexeq12.gif (145x600)

Applying the
Fourier conduction law <see equation 14>
bsexeq14.gif (117x600)

where q is
the heat flux. Typical values for the surface heat loss
coefficient h
for low temperature differences are 5 W/[m.sup.2][degrees]C in still air to
over 15
W/[m.sub.2][degrees]C in a more moderate 3 m/s wind (3). Thus for values of k
of
roughly 1.0
W/mK and values of [h.sub.1] and [h.sub.2] of 5 W/[m.sub.2][degrees]C, the
surface heat
loss
coefficient plays a major, if not dominant, role for thicknesses s up
to 0.50 m and
more. However, for this geometry, increasing s reduces heat
loss over the
entire range of values, unlike other geometries presented
below.
TABLE 1
Typical Property Values at
20[degrees]C
k
[rho]
[C.sub.p]
Material
W/mk
kg/[m.sup.3] J/LGK
Metals
aluminum alloys
110-200
2600-2800 850-900
steel alloys
12-70
7700-8000 450-480
average 35
Nonmetallic Solids
brick
0.38-0.52
1760-1810 840
clay
1.28
1460
880
cement
0.8-1.4
1900-2300 880
hardwood (ash)
0.17-0.21
609-800 2390
sandstone
1.6-2.1
2160-2300 710
Insulators
cardboard
0.064
-- --
(corrugated)
charcoal
0.05
0.3-0.5
670
cotton
0.059
80
1300
fiber board
(insulating)
0.048
237 --
glass wool
0.04
200 670
wood felt
0.05
330
--
Liquids
water
0.597
1000 4180
Gases
air
0.0262
1.177
1005.7
Reference (1)
Two other
brief points. First, it should be noted that, comparing
equations
(10) and (14), thermal resistances can be added generally in the
manner
<see equation below>
bsex132.gif (97x285)

Where
[delta]T is the temperature difference.
Secondly, the
small surface heat loss coefficient h and its extreme
sensitivity
to the wind are both features of it being determined by a
surface
boundary layer of still air with thermal conductivity k=.026 W/mK.
Heat Flow
through the Walls of a Cylindrical Combustion Chamber
Equations (1)
and (3) give for the steady state of an infinite cylinder: <see equation
15>
bsexeq15.gif (67x600)

which has
solutions of the form <see equation 16>
bsexeq16.gif (84x600)

Where 1n is
the natural logarithm.
For inner and
outer wall temperatures of [T.sub.1] and [T.sub.2]
respectively,
then <see equation 17>
bsexeq17.gif (94x600)

where L is
the length of the portion of the cylinder considered and the
cylinder is
assumed to be infinitely long (no end losses).
For the case
where there is a gas at temperature [T.sub.1] inside the cylinder
and one at
[T.sub.2] outside, with surface heat loss coefficients of [h.sub.1] and
[h.sub.2],
and
T=a1n(r)+b <see equation below>
bsexeq18.gif (145x600)

with
solutions: <see equation 19>
bsexeq19.gif (200x600)

The heat loss
from this cylindrical combustion chamber per unit length and
temperature
difference is given by: <see equation 21>
bsexeq21.gif (94x600)

Assuming that
[h.sub.1] = 15 W/[m.sup.2][degrees]C; [r.sub.1]=0.1 m; [h.sub.2]=5
W/[m.sup.2][degrees]C; k=1.0 W/n[degrees]C then
equation (21)
gives the values shown in Table 2.
It is
interesting to note (Table 2) that the heat loss Q actually increases
for 0.12<r<0.30
m and does not fall below its value at [r.sub.2]=0.12
until
[r.sub.2][nearly equal to]0.37 or a 27 cm thick wall. However, to reach this
steady state
condition
itself requires a tremendous amount of heat, an amount increasing
with wall
thickness. Thus, as shown in more detail below, it is
preferable to
keep such walls thin.
One can
similarly look at the functional dependence of Q on other parameters:
for [h.sub.1]
= 15 W/[m.sup.2][degrees]C; [r.sub.1] = 0.12 m; [h.sub.2] = 5
W/[m.sup.2][degrees]C, equation (21) gives the
values shown
in Table 3.
Thus, to
significantly reduce the heat loss by the wall, the conductivity
of the
material in the wall must be made quite low, i.e., k<[near equal to]0.1
W/m[degrees]C.
TABLE 2
Values For Equation (21)
Q
[r.sub.2]
--------------
2[pi]L[delta]T
(m)
(W/m[degrees]C)
0.12
.398
0.14
.411
0.16
.419
0.18
.423
0.20
.424
0.25
.420
0.30
.411
0.35
.401
0.40
.392
0.45
.382
0.50
.374
0.60
.358
0.70
.345
0.80
.334
1.00
.315
TABLE 3
Values For Equation (21)
k
Q
-------------
2[pi]L[delta]T
(W/m[degrees]C)
(W/m[degrees]C)
0.1
.241
0.5
.371
1.0
.398
5.0
.422
10.0
.425
50.0
.428
Spherical
Geometry
A similar set
of calculations can be done for a closed sphere (i.e., a
closed
massive stove with a proportionately small pot).
In this case
<see equation 22>
bsexeq22.gif (84x600)

and has
solutions of the form <see equation below>
bsex134.gif (87x317)

Using the
same boundary conditions as (11) above, this gives solutions of
the form
<see equation below>
bsexeq23.gif (200x393)

With
[h.sub.1] = 15 W/[m.sub.2][degrees]C; [h.sub.2]=5 W/[m.sub.2][degrees]C;
[r.sub.1]=0.1 m;
k = 1.0
W/m[degrees]C as parameters, equation (24)
gives the
values shown in Table 4.
In this case,
the heat loss with increasing
radius is
even more severe than in the case
of the
cylinder above. The reason is that
the surface
heat loss is now increasing at
a rate of [r.sup.2]
[sub.2] for the sphere compared to a
rate of
[r.sub.2] for the cylinder. Further, the
insulating
value of the wall <see equation below>
bsexeq24.gif (84x256)

is increasing
only very slowly compared to the cylinder's insulating
value:
<see equation below>
bsex135.gif (108x150)

Knowing the
temperature distribution the energy required to reach that
steady state
level can also be calculated.
The change in
heat stored in a body is generally given by: <see equation 25>
bsexeq25.gif (84x600)

where dV is a
volume element and [T.sub.2] is the initial temperature of the
volume
element.
For a typical
metal stove, for example, one might find: <see equation below>
bsexeq26.gif (145x600)

TABLE 4
Heat Loss From a Sphere
As a Function of Radius
[r.sub.2]
Q
-------------------
[T.sub.1]-[T.sub.2]
0.12
0.565
0.14
0.638
0.16
0.689
0.18
0.723
0.20
0.754
0.25
0.793
0.30
0.808
0.35
0.814
0.40
0.815
0.45
0.814
0.50
0.813
....
.....
0.70
0.804
....
.....
1.00
0.793
Wood has roughly
18,000 kJ/kg of energy in it so this is the equivalent of
22.5 gm of
wood in energy to heat the stove to its steady state condition.
In contrast,
for a typical cylindrical massive stove one might find <see equation
below>
bsexeq27.gif (105x393)

Again using
L=0.3 m; [rho]=2000 kg/[m.sup.3]; [c.sub.p]=0.880 J/kgK; one finds dE-22 MJ
or the
equivalent of 1.22 kg of wood in energy.
Transient
Heat Loss Calculations
The above
calculations for beat loss were based on the steady state
condition
which for massive walls can only be achieved after several hours
of operation.
The time to reach this steady state condition can be easily
estimated in
the special case of the metal cylinder where there are no
thermal
gradients of significance. In this case
the temperature rise of
the metal
cylinder can be calculated by comparing its specific heat to the
total heat
gain -- the heat flux in minus the heat flux out. Thus <see equation
below>
bsexeq28.gif (94x353)

where V is
the volume of metal in the stove with a density [rho] and a
specific heat
of [c.sub.p], and [A.sub.1] and [A.sub.2] are the inner and outer surface
areas,
[A.sub.1][nearly
equal to][A.sub.2]; [T.sub.1] and [T.sub.2] are the interior and exterior gas
temperatures with
surface
convective heat loss coefficients of [h.sub.1] and [h.sub.2]. Solving for T
gives <see
equation 29>
bsexeq29.gif (67x600)
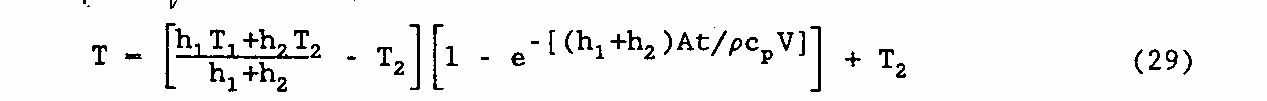
Where e is
the base for natural logarithms, e=2.71828.
The
characteristic time for this system, the time for it to reach (1- 1/e)
of its steady
state value, is given by the inverse of the exponent of (29) <see equation
below>
bsexeq30.gif (94x600)

For the same
stoves as in Table 5 with [h.sub.2]=5 W/[m.sup.2][degrees]C;
[[rho].sub.massive]=2000 kg/[m.sub.3];
[c.sub.massive]=0.880
J/kg[degrees]C; [rho].sub.metal]=8000 kg/[m.sup.3]; [c.sub.metal]=450
J/kg[degrees]C.
[t.sub.c] = 6 minutes
metal stove
[t.sub.c] = 4.9 hours
massive stove
Certainly,
this approach is not correct for the massive stove as there are
significant
temperature gradients within its walls, but it does indicate
the rough
order of time needed to reach steady state in a massive stove.
A more
general calculation which takes into account the thermal gradients
in the
massive stove walls is given below.
Numerical
Techniques
Consider now
the more general case of transient heat loss where the
temperature
gradients in the wall are included. Returning, <see equation below>
bsex137.gif (121x600)

where
[T.sub.g] is the temperature of the hot gas and [T.sub.a] is ambient
temperature.
Such
equations and non-homogenous boundary conditions are straight forward
to solve
using integral transform techniques. Reference (4) gives their
general
solution in several different coordinate systems. However, these
solutions are
generally transcendental equations and it is easier to
simply
generate a numerical solution directly from equations (1) and (11).
The numerical
analysis is begun by dividing a cylindrical wall into small
concentric
sections. The cross section of the wall is shown in Figure 4.
bse4x130.gif (437x600)

Ignoring end
effects, the heat conduction equation for this cylindrically
symmetric
geometry becomes <see equation 31>
bsexeq31.gif (105x600)

Standard
numerical procedures (4) give for the temperature [mm] at point i
(figure 4
indicates how i is determined) and time n <see equation below>
bsexeq32.gif (200x600)

Where
[omicron]() is the order of the truncation error resulting from terminating
the series
expansion.
Using these
<see equations 35> equations, for points inside the wall
bsexeq35.gif (105x600)

where the
value [r.sub.i] is given by i[delta]r or, equivalently, <see equation 36>
bsexeq36.gif (60x600)

At the
surface the boundary conditions, equation (11), are, <see equation below>
bsex138.gif (167x437)

to get at the
inner surface, i=[i.sub.1] <see equation 37>
bsexeq37.gif (75x600)

and at the
outer surface i-[i.sub.2] <see equation 38>
bsexeq38.gif (75x600)

rather than
equation (36).
Several
simple modifications of this are possible to more accurately
reflect the
conditions within a stove.
First, at
both the inner and outer surfaces the convective heat transfer
boundary
conditions can be modified to include radiant heat transfer.
Modifying
equation C-12, this can be written as <see equation 39a>
bsexeq39.gif (75x600)

where
i=[i.sub.1], that is, i is the inner surface; and <see equation below>
bsexeq40.gif (84x437)

for
i=[i.sub.2], the outer wall. In these equations, [sigma] is the
Stefan-Boltzmann
constant, A
is the area of the pot bottom and firebed, and [F.sub.fw] is the view
factor
between the firebed and the combustion chamber wall. The factor [beta]
reduces the
effective size of the fire as it does not generally cover the
entire
firebed but more usually only the center half diameter. [T.sub.f] is the
temperature
at which the firebed radiates and [T.sub.p] is the pot temperature.
In the second
equation, [[epsilon].sub.w] is the emissivity and A is the area of the
wall. The
emissivity is missing in the first equation because it is
assumed equal
to 1. This is reasonable as the interior will be blackened
and further
this assumption avoids the complications of multiple reflections
on the inside
surfaces. The view factor F is missing in the second
equation
because it is equal to 1.0 -- the stove is radiating uniformly
out in all
directions. Finally, it should be noted that the temperatures
and heat
losses predicted by this program are for the combustion chamber
only and only
for a single stove power -- usually high. To predict the
values for an
entire stove the exterior area and interior area exposed to
the hot gases
must be increased appropriately while keeping the interior
area exposed
to the radiant heat of the fire the same.
The second
modification accounts for the increasing heat loss from the
exterior
surface as it warms due to increasing convective heat transfer.
Warm air
rises. The hotter the exterior wall the more it warms the
adjacent
ambient air and the faster it rises, increasing the convective
heat transfer
to it even more. Correlations for this factor, natural convection
by a heated
vertical plate or cylinder, are given in most basic
texts and are
listed in Appendix B. The form used here for the exterior
convective
heat transfer coefficient is from reference (5): <see equation below>
bsex139.gif (108x393)

where
i=[i.sub.2], and L is the height of the plate, or in this case, the combustion
chamber.
The
performance of the bare metal stove, in particular, will be affected
by this
variable exterior heat transfer coefficient due to its generally
higher
temperatures. Similarly, the performance of the bare metal stove
will be more
strongly affected by the wind than will the performance of
insulated
metal, fired clay, or concrete stoves. However, as cooking is
almost always
done in protected locations this is not expected to be an
important
consideration.
To reduce the
heat loss of the bare metal wall, double wall geometries
with a dead
air space can be considered. For this case the same equations
as above
apply for each wall separately, but the boundary conditions
between the
two walls must be modified. In particular, the effective heat
transfer
coefficient across a dead air space is given empirically by
reference
(5). <see equation 41>
bsexeq41.gif (117x600)

where [delta]
is the space between the two walls, CH is the combustion chamber
height, and
[T.sub.1] and [T.sub.2] are the surface temperatures of the two facing
walls.
Alternatively,
lightweight insulants can be used. Again the above equations
are used
twice, first to calculate the heat conduction through the
first wall,
then through the insulation. In this case, the boundary
condition
between the walls and insulant is given by setting their facing
surfaces at
the same temperature (removing the radiative and convective
heat transfer
terms), and setting their heat fluxes equal at the surface
between the
two walls; <see equation 42>
bsexeq42.gif (94x600)

where
[k.sub.1], [T.sub.1] and [k.sub.2], [T.sub.2] are the thermal conductivities
and temperatures of
the wall and
insulant at the point of contact.
Computer
programs in Microsoft basic for the Apple Macintosh are listed
below along
with a table (Table 5) of the parameters used. The output is
bsextab5.gif (600x600)

presented in
the figures in the text, chapter III, and discussed there.
In addition,
to the graphs of computer output presented in Chapter III,
other data of
interest that has been generated by this numerical routine
include: The
integrated wall loss as a function of time; The wall loss
as a function
of different levels of interior wall convective or radiative
heat loads;
and radiant transfer from the wall to the pot (Appendix C).
The numerical
routine discussed above is stable (4) if <see equation 43>
bsexeq43.gif (84x600)

The numerical
routine was also tested to ensure that it converged to exact
steady-state
analytical solutions and did so independently of the size of
the time
step, t, or node size, r. Convergence was excellent in all cases
tested. The
primary drawback of this numerical routine, however, was the
very small
time steps necessary when [alpha] was large -- such as for metal
stoves. This
led to run times of several hours in such cases. Among the
methods
available for speeding up this calculation in such cases are using
"compiled"
rather than "interpreted basic" and by careful optimisation of
the computer
code itself. These tasks are left to the interested reader.
COMPUTER
PROGRAMS FOR COMBUSTION CHAMBER WALL LOSS
Program 1:
1 REM THIS PROGRAM CALCULATES THE HEAT
LOSS FROM A SINGLE WALL CYLINDRICAL COMBUSTION CHAMBER
5 CLS: BEEP
7 CLEAR
50 OPEN "LPT1:" FOR OUTPUT AS #1
89 PRINT "ENTER THE NUMBER OF NODAL
POINTS FOR THE TEMPERATURE TO BE CALCULATED AT IN THE WALL"
90 INPUT "ENTER NUMBER OF STEPS S IN
X, S)=2, S="; S
91 PRINT #1, "THE NUMBER OF
TEMPERATURE NODAL POINTS IS "; S
92 REM FOR A CONCRETE STOVE S IS TYPICALLY
1 PER CM; FOR A METAL STOVE 1 PER MM.
99 REM THE TWO MATRICES TT(I) AND TN(I)
ARE THE VALUES OF THE TEMPERATURE AT THE CURRENT TIME,
TT, AND THE NEXT TIME, TN
100 DIM TT(S), TN(S)
150 PRINT "ENTER INNER AND OUTER
RADIUS AND HEIGHT OF THE COMBUSTION CHAMBER"
151 INPUT "ENTER RA, RZ, CH";
RA, RZ, CH
152 PRINT #1, "THE COMBUSTION CHAMBER
DIMENSIONS ARE"
153 PRINT #1, "RA="; RA,
"RZ="; RZ, "CH="; CH
154 REM FOR A CONCRETE STOVE TYPICAL
VALUES ARE RA=.15, RZ=.25, AND CH=.15
199 PRINT "ENTER INNER CONVECTIVE
HEAT TRANSFER COEFFICIENT AND EXTERNAL EMISSIVITY OF STOVE"
200 INPUT "ENTER HA, EE"; HA, EE
201 PRINT #1, "THE INNER CONVECTIVE
HEAT TRANSFER COEFFICIENT AND EXTERNAL EMISSIVITY ARE"
202 PRINT #1, "HA="; HA,
"EE="; EE
203 REM THE EMISSIVITIES OF THE INTERIOR
WALL, THE FIRE, AND AMBIENT ARE ASSUMED TO BE 1.0
204 REM HA IS TYPICALLY 10 AND EE IS .1 TO
1.
209 PRINT "ENTER THE HEAT CAPACITY,
DENSITY, AND THERMAL CONDUCTIVITY OF THE STOVE WALL"
210 INPUT "ENTER HC, HD, HK";
HC, HD, HK
211 PRINT #1, "THE HEAT CAPACITY,
DENSITY, AND THERMAL CONDUCTIVITY OF THE WALL ARE"
212 PRINT #1, "HC="; HC,
"HD="; HD, "HK="; HK
213 REM FOR A CONCRETE STOVE TYPICAL
VALUES ARE HC=880, HD=2000, AND HK=1.
219 PRINT "ENTER TIME INCREMENT,
TOTAL NUMBER OF TIME INCREMENTS TO BE CALCULATED THROUGH, AND
THE P'th TIME INTERVAL TO BE
PRINTED"
220 INPUT "ENTER DT, NT, PT";
DT, NT, PT
221 PRINT #1, "THE TIME INCREMENT,
THE TOTAL NUMBER OF INCREMENTS, AND THE PRINT TIMES ARE"
222 PRINT #1, "DT="; DT,
"NT="; NT, "PT="; PT
223 REM TYPICAL VALUES FOR A CONCRETE
STOVE ARE DT=60, NT=600, AND PT =20. FOR METAL STOVES DT
IN PARTICULAR MUST BE DRASTICALLY
REDUCED TO ROUGHLY .04
400 DR=(RZ-RA)/S 'THIS IS THE INCREMENT IN
THE RADIUS BETWEEN NODES
420 I1=RA/DR 'THIS IS THE VALUE OF THE
FIRST NODE, MEASURING FROM THE ORIGIN IN UNITS OF DR
430 AA=HK/(HD*HC) 'THIS IS THE THERMAL
DIFFUSIVITY
500 BB=AA*DT/DR^2 'His IS THE STABILITY
FACTOR FOR THE DIFFERENCE EQUATIONS BELOW
510 PRINT #1, "THE STABILITY FACTOR
IS", USING "##.### ^^^^"; BB
511 REM THE STABILITY FACTOR MUST BE LESS
THAN 0.5
520 IF BB)=.5 6070 220
529 PRINT "SET THE AMBIENT, GAS, AND
FIRE TEMPERATURES"
530 INPUT "ENTER TA, TG, TF";
TA, TG, TF
531 PRINT #1, "THE AMBIENT, GAS, AND
FIRE TEMPERATURES ARE"
532 PRINT #1, "TA=";TA,
"TG="; TG, "TF="; TF
533 REM TYPICAL VALUES ARE TA=300, TG=700,
AND TF=1000
550 SGM=.000000056697# 'THE
STEFAN-BOLTZMANN CONSTANT 5.6697D-08
551 TP=373 'THE POT TEMPERATURE IN DEGREES
KELVIN
552 FV1=(CH/RA)^2+2!
553
FV--RA*(1!-.5*(FV1-(FV1^2-4!)^.5))/(2*CH) 'THE RADIANT VIEWFACTOR BETWEEEN THE
FIREBED AND ST
OVE WALL
554 PRINT #1, "THE VIEWFACTOR IS
"; FV
560 FOR I=0 TO S STEP 1 'SET THE TEMPERATURES
TO AMBIENT
561 TT(I)=TA
562 TN(I)=TA
563 NEXT I
600 BA=2!*DR*HA/HK 'THIS FACTOR IS FOR THE
INTERIOR SURFACE CONVECTIVE HEAT TRANSFER
630 P=1! 'P IS A TALLY SO THAT VALUES ARE
PRINTED WHEN EACH PT-th VALUE IS REACHED
640 TOTQ--0 'THIS IS THE INTEGRATED HEAT
LOSS
650 PRINT #1, " TIME "; 'A
COLUMN HEADING
651 FOR JS=O TO S STEP I 'COLUMN HEADINGS
652 PRINT #1, "TEMP";JS;
653 NEXT JS
654 PRINT #1, " HEAT LOSS";
'COLUMN HEADING
655 PRINT #1, " TOTAL " 'COLUMN
HEADING
700 FOR W-1 TO NT STEP 1 'ITERATE THROUGH
THE VALUES OF TIME
705 REM CALCULATE THE INTERIOR WALL
SURFACE TEMPERATURE
708 REM THE FACTOR .5 TIMES TF IS USED TO
ACCOUNT FOR FIRE BEING LIMITED TO CENTER HALF DIA
METER OF STOVE, ITS SELF SHIELDING,
AND OTHER FACTORS REDUCING ITS RADIANT FLUX TOWARD
WALL. THE SAME VIEWFACTOR HAS BEEN
USED REGARDLESS.
709
BAR=2!*DR*SGM*FV*(.5*TF^4+TP^4-2!*TT(0)^4)/HK 'INTERIOR RADIATIVE HEAT TRANSFER
710 TN(0)=BB*((1-1/(2*11))*(TT(1)+BAR+BA*(TG-TT(0)))-2*TT(0)+(1+1/(2*I1))*TT(1))+TT(0)
740 SM=S-1
750 FOR I=1 TO SM STEP 1 'CALCULATE THE
TEMPERATURES FOR THE NODES INSIDE THE WALL SUCCESSIVELY
755 I2=I1+I 'NOTE THAT MATRIX VALUES TT(I)
START FOR I=O WHILE THE WALL POSITION STARTS AT I1+I
760
TN(I)=BB*((1-1/(2*I2))*TT(I-1)-2*TT(I)+(1+1/(2*I2))*TT(I+1))+TT(I)
765 NEXT I
790 19=I1+S
791 REM CALCULATE THE EXTERIOR WALL
SURFACE TEMPERATURE
792
BZ=2!*DR*1.42*(TT(S)-TA)^.25/(HK*CH^.25) 'EXTERIOR CONVECTIVE HEAT TRANSFER
COEFFICIENT
793 REM THE VIEWFACTOR TO AMBIENT IS 1.0
794 BZR=2!*DR*EE*SGM*(TT(S)^4-TA^4)/HK
'EXTERIOR RADIATIVE HEAT TRANSFER
795
TN(S)=BB*((1-1/(2*I9))*TT(SM)-2*TT(S)+(1+1/(2*I9))*(TT(SM)-BZR+BZ*(TA-TT(S))))+TT(S)
799 REM CALCULATE THE HEAT LOSS INTO THE
INNER WALL OF THE COMBUSTION CHAMBER.
800
QQ=-CH*HK*RA*6.283185#*(TN(1)-TN(0))/DR
801 TOTQ=TOTQ+QQ*DT
900 X=P*PT
910 IF N<X GOTO 1000 'CHECK TO SEE IF
VALUE OF PT IS CROSSED AND WHETHER OR NOT TO PRINT NODE
TEMPERATURES
920 QT=N*DT/60 'THE TIME IN MINUTES
925 PRINT #1, USING "####.##";
QT;
930 FOR IZ=0 TO S STEP 1
936 PRINT #1, USING "#####.#";
TN(IZ);
937 NEXT IZ
938 PRINT #1, USING
"#######.##"; QQ;
940 PRINT #1, USING "########.#";
TOTQ
950 P=P+1 'SET P TO PICK OUT NEXT VALUE PT
FOR PRINTING
1000 FOR 1=0 TO S STEP 1
1010 TT(I)=TN(I) 'SET TEMPERATURES, TT,
FOR CURRENT TIME EQUAL TO THOSE, TN, FOR FUTURE TIME IN
PREPARATION FOR NEXT ITERATION
1020 NEXT I
1100 NEXT N
1499 BEEP
1500 END
Program 2:
1 REM THIS PROGRAM CALCULATES HEAT LOSS
FROM A DOUBLE WALL CYLINDRICAL COMBUSTION CHAMBER
5 CLS
7 CLEAR
50 OPEN "LPT1:" FOR OUTPUT AS #1
55 PRINT "ALL UNITS ARE IN KILOGRAMS,
METERS, AND SECONDS"
89 PRINT "ENTER NUMBER OF NODES FOR
TEMPERATURE TO BE CALCULATED AT IN WALLS"
90 INPUT "ENTER NUMBER OF NODES,
>=2, IN WALL 1, S, WALL 2, ZS"; S, ZS
91 PRINT #1, "THE NUMBER OF
TEMPERATURE NODES IN THE WALLS ARE "; S, ZS
92
REM FOR A MASSIVE STOVE, S IS TYPICALLY 1 PER CM; FOR A METAL STOVE 1 PER MM.
99 REM THE MATRICES TT(I), TN(I), ZTT(ZI),
AND ZTN(ZI) ARE THE VALUES OF THE TEMPERATURE AT THE
CURRENT TIME, TT& ZTT, AND THE NEXT
TIME, TN & ZTN
100 DIM TT(S), TN(S), ZTT(ZS), ZTN(ZS)
150 PRINT "ENTER INNER AND OUTER
RADIUS OF INNER WALL"
151 INPUT "ENTER RA, RZ"; RA, RZ
152 PRINT #1, "INNER WALL RADII ARE
";
153 PRINT #1, "R4="; RA,
"RZ="; RZ
155 PRINT "ENTER INNER AND OUTER
RADIUS OF OUTER WALL"
156 INPUT "ENTER ZRA, ZRZ"; ZRA,
ZRZ
157 PRINT #1, "OUTER WALL RADII ARE
";
158 PRINT #1, "ZRA="; ZRA,
"ZRZ="; ZRZ
160 PRINT "ENTER COMBUSTION CHAMBER
HEIGHT"
161 INPUT "ENTER CH"; CH
162 PRINT #1, "COMBUSTION CHAMBER
HEIGHT IS ; CH
170 PRINT "ENTER INNER CONVECTIVE
HEAT TRANSFER COEFFICIENT"
171 INPUT "ENTER HA"; HA
172 PRINT #1, "THE INNER CONVECTIVE
HEAT TRANSFER COEFFICIENT IS "; HA
175 PRINT "ENTER EFFECTIVE EMISSIVITY
BETWEEN THE WALLS AND THE OUTER WALL EXTERNAL EMISSIVITY"
176 INPUT "ENTER EE, ZEE"; EE,
ZEE
177 PRINT #1, "RADIATIVE COUPLING
BETWEEN WALLS, AND EXTERIOR EMISSIVITY ARE"
178 PRINT #1, "EE="; EE,
"ZEE="; ZEE
179 REM THE EMISSIVITIES OF INTERIOR
SURFACE, FIRE AND AMBIENT ARE ASSUMED TO BE 1.0
180 PRINT "ENTER HEAT CAPACITY,
DENSITY, AND THERMAL CONDUCTIVITY OF INNER WALL"
181 INPUT "ENTER HC, HD, HK";
HC, HD, HK
182 PRINT #1, "THE HEAT CAPACITY,
DENSITY AND THERMAL CONDUCTIVITY OF THE INNER WALL ARE"
183 PRINT #1, "HC="; HC,
"HD="; HD, "HK="; HK
190 PRINT "ENTER HEAT CAPACITY,
DENSITY, AND THERMAL CONDUCTIVITY OF OUTER WALL"
191 INPUT "ENTER ZHC, ZHD, ZHK";
ZHC, ZHD, ZHK
192 PRINT #1, "THE HEAT CAPACITY,
DENSITY AND THERMAL CONDUCTIVITY OF THE OUTER WALL ARE"
193 PRINT #1, "ZHC="; ZHC,
"ZHD="; ZHD, "ZHK="; ZHK
200 PRINT "ENTER THE AMBIENT, GAS,
AND FIRE TEMPERATURES"
201 INPUT "ENTER TA, TG, TF";
TA, TS, TF
202 PRINT #1, "THE AMBIENT, GAS, AND
FIRE TEMPERATURES ARE"
203 PRINT #1, "TA="; TA,
"TG="; TG, "TF="; TF
210 PRINT "ENTER TIME INCREMENT,
TOTAL NUMBER OF TIME INCREMENTS TO BE CALCULATED THROUGH, AND
THE P'th TIME INTERVAL TO BE
PRINTED"
211 INPUT "ENTER DT, NT, PT";
DT, NT, PT
212 PRINT #1, "THE TIME INCREMENT,
THE TOTAL NUMBER OF INCREMENTS, AND THE PRINT TIMES
213 PRINT #1, "DT="; DT,
"NT="; NT, "PT="; PT
300 TOTQ=O! 'THIS IS THE INTEGRATED HEAT
LOSS
400 DR=(RZ-RA)/S : ZDR=(ZRZ-ZRA)/ZS 'THIS
IS THE INCREMENT IN THE RADIUS BETWEEN NODES
420 I1=RA/DR : ZI1=ZRA/ZDR 'VALUE OF FIRST
NODE, MEASURING FROM ORIGIN IN UNITS OF DR
421 QI1P=1+1/(2*I1) : ZQI1P=1+1/(2*ZI1)
422 GI1M=1-1/(2*I1) : ZQI1M=1-1/(2*ZI1)
423 GI2P=1+1/(2*(I1+S)) :
ZQI2P=1+1/(2*(ZI1+ZS))
424 QI2M-1-1/(2*(I1+S)) : ZQI2M=1-1/(2*(2I1+ZS))
426 SM=S-1 : ZSM-ZS-1
430 AA=HK/(HD*HC) : ZAA=ZHK/(ZHD*ZHC)
'THIS IS THE THERMAL DIFFUSIVITY
500 BB=AA*DT/DR^2 : ZBB--ZAA*DT/ZDR^2
'STABILITY FACTORS FOR DIFFERENCE EQUATIONS BELOW
510 PRINT #1, "THE STABILITY FACTOR
IS"; BB, ZBB
511 REM THE STABILITY FACTOR MUST BE LESS
THAN 0.5
520 IF BB>=.5 GOTO 211
521 IF ZBB>=.5 GOTO 211
550 SGM=.000000056697# 'THE
STEFAN-BOLTZMANN CONSTANT 5.6697D-08
551 TP=373 'THE POT TEMPERATURE IN DEGREES
KELVIN
552 FV1=(CH/RA)^2+2!
553
FV-RA*(1!-.5*(FV1-(FV1^2-4!)^.5))/(2!*CH) 'THE RADIANT VIEWFACTOR BETWEEEN THE
FIREBED AND S
TOVE WALL
554 PRINT #1, "THE VIEWFACTOR IS
"; FV
560 FOR I-0 TO S STEP 1 'SET THE
TEMPERATURES TO AMBIENT
561 TT(I)=TA
562
Tn(I) =TA
563
NEXT I
570
FOR ZI=O TO ZS STEP 1
571
ZTT(ZI)=TA : ZTN(ZI)=TA
572
NEXT ZI
600
BA=2!*DR*HA/HK 'THIS FACTOR IS FOR THE
INTERIOR SURFACE CONVECTIVE HEAT TRANSFER
630
P=1! 'P IS A TALLY SO THAT VALUES ARE
PRINTED WHEN EACH PT-th VALUE IS REACHED
649
SZS=S + ZS + 1
650
PRINT #1, " TIME
";'COLUMN HEADING
651
FOR JS=O TO SZS STEP 1 'COLUMN HEADINGS
652
PRINT #1, "TEMP";JS;
653
NEXT JS
654
PRINT #1, "
HEAT LOSS"; 'COLUMN HEADING
655
PRINT #1, "
TOTAL " 'COLUMN HEADING
700
FOR N-1 TO NT STEP 1 'ITERATE THROUGH THE
VALUES OF TIME
705
REM CALCULATE THE INTERIOR WALL SURFACE
TEMPERATURE
708
REM THE FACTOR .5*TF USED 70 ACCOUNT FOR
FIRE BEING LIMITED TO CENTER HALF DIAMETER OF
STOVE, ITS SELF SHIELDING, AND OTHER
FACTORS REDUCING ITS RADIANT FLUX TOWARD THE WALL. THE
SAME VIEWFACTOR HAS BEEN USED REGARDLESS.
709
BAR=2!*DR*SGM*FV*(.5*TF^4+TP^4-2!*TT(0)^4)/HK 'INTERIOR RADIATIVE HEAT
TRANSFER
710
TN(0)=BB*(QIIM*(TT(1)+BAR+BA*(TG-TT(0)))-2*TT(0)+Q11P*TT(1))+TT(0)
740
SM=S-1
750
FOR 1=1 TO SM STEP 1 'CALCULATE THE
TEMPERATURES FOR THE NODES INSIDE THE WALL SUCCESSIVELY
755
12=1/(2*(I1+I))
760
TN(I)=BB*((1-12)*TT(I-1)-2*TT(I)+(I+I2)*TT(I+1))+TT(I)
765
NEXT I
791
REM CALCULATE THE EXTERIOR WALL SURFACE
TEMPERATURE
792
BZ=(2!*DR/HK)*3.93*(ZRA-RZ)^-.1389*CH^-.1111*(TT(S)-ZTT(0))^.25/(TT(S)+ZTT(0))^.3171
'EXTERIOR CONVECTIVE HEAT TRANSFER
COEFFICIENT
793
REM THE VIEWFACTOR TO THE OUTER WALL IS 1.0
794
BZR=2!*DR*EE*SGM*(TT(S)^4-ZTT(0)^4)/HK
'EXTERIOR RADIATIVE HEAT TRANSFER
795
TN(S)=BB*(QI2M*TT(SM)-2*TT(S)+QI2P*(TT(SM)-BZR+BZ*(ZTT(0)-TT(S))))*TT(S)
809
ZBAR=2!*ZDR*EE*SGM*(TT(S)^4-ZTT(0)^4)/ZHK
'INTERIOR RADIATIVE HEAT TRANSFER
810
ZTN(0)=ZBB*(ZQI1M*(ZTT(1)+ZBAR+BZ*(TT(S)-ZTT(0)))-2*ZTT(0)+ZQI1P*ZTT(1))+ZTT(0)
850
FOR ZI=1 TO ZSM STEP 1 'CALCULATE
TEMPERATURES FOR NODES INSIDE WALL SUCCESSIVELY
855
Z12--1/(2*(ZII+I))
860
ZTN(ZI)=ZBB*((I-ZI2)*ZTT(2I-1)-2*ZTT(ZI)+(1+Z12)*ZTT(ZI+1))+ZTT(ZI)
865
NEXT ZI
891
REM CALCULATE THE EXTERIOR WALL SURFACE
TEMPERATURE
892
ZBZ=2!*ZDR*1.42*(ZTT(ZS)-TA)^.25/(ZHK*CH^.25)
'EXTERIOR CONVECTIVE HEAT TRANSFER COEFFICIEN
T
893
REM THE VIEWFACTOR TO AMBIENT IS 1.0
894
ZBZR=2!*ZDR*ZEE*SGM*(ZTT(ZS)^4-TA^4)/ZHK
'EXTERIOR RADIATIVE HEAT TRANSFER
895
ZTN(ZS)=ZBB*(2Q12M*ZTT(ZSM)-2*ZTT(ZS)+ZQI2P*(ZTT(ZSM)-ZBZR+ZBZ*(TA-ZTT(ZS))))+ZTT(ZS)
900
REM CALCULATE THE HEAT LOSS INTO THE INNER
WALL OF THE COMBUSTION CHAMBER.
901
QQ=-CH*HK*RA*6.283185#*(TN(1)-TN(0))/DR
902
TOTQ=TOTQ+QQ*DT
905
X=P*PT
910
IF N<X GOTO 1000 'CHECK IF VALUE OF PT IS
CROSSED AND WHETHER TO PRINT NODE TEMPERATURES
920
QT-N*DT/60 'THE TIME IN MINUTES
925
PRINT #1, USING "####.##" ; QT;
930
FOR IZ=O TO S STEP 1
936
PRINT #1, USING "#####.#" ;
TN(IZ);
937
NEXT IZ
938
FOR ZI=O TO ZS STEP 1
939
PRINT #1, USING "#####.#" ;
ZTN(ZI);
940
NEXT ZI
948
PRINT #1, USING "#######.##"; QQ;
949
PRINT #1, USING "#######.#"; TOTQ
950
P=P+1 'SET P TO PICK OUT NEXT VALUE PT FOR
PRINTING
1000
FOR I=O TO S STEP 1
1010
TT(I)=TN(I) 'SET TEMPERATURES FOR NEXT
ITERATION
1020
NEXT I
1030
FOR ZI-0 TO ZS STEP 1
1032
ZTT(ZI)=ZTN(ZI)
1034
NEXT ZI
1100
NEXT N
1499
BEEP
1500
END
Program 3:
1 REM THIS
PROGRAM CALCULATES HEAT LOSS FROM A SINGLE COMPOSITE WALL COMBUSTION CHAMBER
5 CLS
7 CLEAR
50 OPEN
"LPT1:" FOR OUTPUT AS #1
55 PRINT
"ALL UNITS ARE IN KILOGRAMS, METERS, AND SECONDS"
89 PRINT
"ENTER NUMBER OF NODES FOR TEMPERATURE TO BE CALCULATED AT IN WALLS"
90 INPUT
"ENTER NUMBER OF NODES, >=2, IN WALL 1, S, WALL 2, ZS" S, ZS
91 PRINT #1,
"THE NUMBER OF TEMPERATURE NODES IN THE WALLS ARE "; S, ZS
92 REM FOR A
MASSIVE STOVE, S IS TYPICALLY 1 PER CM; FOR A METAL STOVE 1 PER MM.
99 REM THE
MATRICES TT(I), TN(I), ZTT(ZI), AND ZTN(ZI) ARE THE VALUES OF THE TEMPERATURE
AT THE
CURRENT TIME, TT& ZTT, AND THE NEXT
TIME, TN & ZTN
100
DIM TT(S), TN(S), ZTT(ZS), ZTN(ZS)
150
PRINT "ENTER INNER AND OUTER RADIUS OF
INNER WALL"
151
INPUT "ENTER RA, RZ"; RA, RZ
152
PRINT #1, "INNER WALL RADII ARE";
153
PRINT #1, "RA="; RA,
"RZ="; RZ
155
PRINT "ENTER INNER AND OUTER RADIUS OF
OUTER WALL"
156
INPUT "ENTER ZRA, ZRZ"; ZRA, ZRZ
157
PRINT #1, "OUTER WALL RADII ARE";
158
PRINT #1, "ZRA="; ZRA,
"ZRZ="; ZRZ
160
PRINT "ENTER COMBUSTION CHAMBER
HEIGHT"
161
INPUT "ENTER CH"; CH
162
PRINT #1, "COMBUSTION CHAMBER HEIGHT IS
"; CH
170
PRINT "ENTER INNER CONVECTIVE HEAT
TRANSFER COEFFICIENT"
171
INPUT "ENTER HA"; HA
172
PRINT #1, "THE INNER CONVECTIVE HEAT
TRANSFER COEFFICIENT IS "; HA
175
PRINT 'ENTER THE OUTER WALL EXTERNAL
EMISSIVITY"
176
INPUT "ENTER ZEE"; ZEE
177
PRINT #1, "EXTERIOR EMSSIVITY IS"
178
PRINT #1, "ZEE="; ZEE
179
REM THE EMISSIVITIES OF INTERIOR SURFACE,
FIRE AND AMB1ENT ARE ASSUMED TO BE 1.0
180
PRINT "ENTER HEAT CAPACITY, DENSITY,
AND THERMAL CONDUCTIVITY OF INNER WALL"
181
INPUT "ENTER HC, HD, HK"; HC, HD,
HK
182
PRINT #1, "THE HEAT CAPACITY, DENSITY
AND THERMAL CONDUCTIVITY OF THE INNER WALL ARE"
183
PRINT #1, "HC="; HC,
"HD="; HD, "HK="; HK
190
PRINT "ENTER HEAT CAPACITY, DENSITY,
AND THERMAL CONDUCTIVITY OF OUTER WALL"
191
INPUT "ENTER ZHC, ZHD, ZHK"; ZHC,
ZHD, ZHK
192
PRINT #1, "THE HEAT CAPACITY, DENSITY
AND THERMAL CONDUCTIVITY OF THE OUTER WALL ARE"
193
PRINT #1, "ZHC="; ZHC,
"ZHD="; ZHD, "ZHK='; ZHK
200
PRINT "ENTER THE AMBIENT, GAS, AND FIRE
TEMPERATURES"
201
INPUT "ENTER TA, TG, TF"; TA, TO,
TF
202
PRINT #1, "THE AMBIENT, GAS, AND FIRE
TEMPERATURES ARE"
203
PRINT #1, "TA="; TA, "TG=';
TG, "TF="; TF
210
PRINT "ENTER TIME INCREMENT, TOTAL
NUMBER OF TIME INCREMENTS TO BE CALCULATED THROUGH, AND
THE P' th TIME INTERVAL TO BE
PRINTED"
211
INPUT "ENTER DT, NT, PT"; DT, NT,
PT
212
PRINT #1, "THE TIME INCREMENT, THE
TOTAL NUMBER OF INCREMENTS, AND THE PRINT TIMES"
213
PRINT #1, "DT="; DT,
"NT="; NT, "PT="; PT
300
TOTQ=O! 'THIS IS THE INTEGRATED HEAT LOSS
400
DR=(RZ-RA)/S : ZDR=(ZRZ-ZRA)/ZS 'THIS IS THE
INCREMENT IN THE RADIUS BETWEEN NODES
420
I1=RA/DR : ZII=ZRA/ZDR 'VALUE OF FIRST NODE,
MEASURING FROM ORIGIN IN UNITS OF DR
421
QI1P--1+1/(2*11) ; ZQI1P=1+1/(2*ZI1)
422
QI1M=1-1/(2*I1) ; ZQIIM=I-I/(2*ZLL)
423
GI2P=1+1/(2*(I1+S)) : ZQ12P-1+1/(2*(ZII+ZS))
424
Q12M=1-1/(2*(I1+S)) : ZQ12M-1-1/(2*(ZII+ZS))
426
SM=S-1 : ZSM=ZS-1
430
AA=HK/(HD*HC) : ZAA=ZHK/(ZHD*ZHC) 'THIS IS
THE THERMAL DIFFUSIVITY
500
BB=AA*DT/DR^2 : ZBB=ZAA*DT/ZDR^2 'STABILITY
FACTORS FOR DIFFERENCE EQUATIONS BELOW
510
PRINT #1, "THE STABILITY FACTOR
IS"; BB, ZBB
511
REM THE STABILITY FACTOR MUST BE LESS THAN
0.5
520
IF BB)=.5 GOTO 1499
521
IF ZBB)=.5 GOTO 1499
550
SGM.000000056697# 'THE STEFAN-BOLTZMANN
CONSTANT 5.6697D-08
551
TP=373 'THE POT TEMPERATURE IN DEGREES
KELVIN
552
FVI=(CR/RA)^2+2!
553
FV=RA*(1!-.5*(FV1-(FV1^2-4!) ^.5))/(2*CH)
'THE RADIANT VIEWFACTOR BETWEEEN THE FIREBED AND ST
OVE
WALL
554
PRINT #1, 'THE VIEWFACTOR IS "; FV
560
FOR I=0 TO S STEP 1 'SET THE TEMPERATURES TO
AMBIENT
561
TT(I)=TA
562
TN(1) =TA
563
NEXT I
570
FOR ZI=O TO ZS STEP 1
571
ZTT(ZI)=TA : ZTN(ZI)=TA
572
NEXT ZI
600
BA=2!*DR*HA/HK 'THIS FACTOR IS FOR THE
INTERIOR SURFACE CONVECTIVE HEAT TRANSFER
630
P=1! 'P IS A TALLY SO THAT VALUES ARE
PRINTED WHEN EACH PT-th VALUE IS REACHED
649
SZS=S + ZS + 1
650
PRINT #1, " TIME
"; 'A COLUMN HEADING
651
FOR JS=0 TO SZS STEP 1 'COLUMN HEADINGS
652
PRINT #1, "TEMP";JS;
653
NEXT JS
654
PRINT #1, " HEAT LOSS"; 'COLUMN
HEADING
655
PRINT #1, "
TOTAL " 'COLUMN HEADING
700
FOR N=1 TO NT STEP 1 'ITERATE THROUGH THE
VALUES OF TIME
705
REM CALCULATE THE INTERIOR WALL SURFACE
TEMPERATURE
708
REM THE FACTOR .5*TF USED TO ACCOUNT FOR
FIRE BEING LIMITED TO CENTER HALF DIAMETER OF
STOVE, ITS SELF SHIELDING, AND OTHER
FACTORS REDUCING ITS RADIANT FLUX TOWARD THE WALL. THE
SAME VIEWFACTOR HAS BEEN USED REGARDLESS.
709
BAR=2!*DR*SGM*FV*(.5*TF^4+TP^4-2!*TT(0)^4)/HK 'INTERIOR RADIATIVE HEAT TRANSFER
710
TN(0)=88*(QI1M*(TT(1)+BAR+BA*(TG-TT(0)))-2*TT(0)+QI1P*TT(1))+TT(0)
750 FOR I=1
TO SM STEP 1 'CALCULATE THE TEMPERATURES FOR THE NODES INSIDE THE WALL
SUCCESSIVELY
755
12=I/(2*(I1+I))
760
TN(I)=BB*((1-I2)*TT(I-1)-2*TT(I)+(1+I2)*TT(I+1))+TT(I)
765
NEXT I
791
REM CALCULATE THE EXTERIOR WALL SURFACE
TEMPERATURE
795
TN(S)=BB*(Q12M*TT(SM)-2*TT(S)+QI2P*(TT(SM)+DR*ZHK*(ZTT(1)-TT(SM))/(ZDR*HK)))+TT(S)
800
ZTN(0)=TN(S)
850
FOR ZI=1 TO ZSM STEP 1 'CALCULATE
TEMPERATURES FOR NODES INSIDE WALL SUCCESSIVELY
855
ZI2=1/(2*(ZII+I))
860
ZTN(ZI)=ZBB*((1-Z12)*ZTT(ZI-1)-2*ZTT(ZI)+(1+ZI2)*ZTT(ZL+1))+ZTT(ZI)
865
NEXT ZI
891
REM CALCULATE THE EXTERIOR WALL SURFACE
TEMPERATURE
892
ZBZ=2!*ZDR*1.42*(ZTT(ZS0-TA)^.25/(ZHK*CH^.25) 'EXTERIOR CONVECTIVE HEAT
TRANSFER COEFFICIENT
893
REM THE VIEWFACTOR TO AMBIENT IS 1.0
894
ZBZR=2!*ZDR*ZEE*SGM*(ZTT(ZS)^4-TA^4)/ZHK
'EXTERIOR RADIATIVE HEAT TRANSFER
895
ZTN(ZS)=ZBB*(ZGI2M*ZTT(ZSM)-2*ZTT(ZS)+ZQI2P*(ZTT(ZSM)-ZBZR+ZBZ*(TA-ZTT(ZS))))+ZTT(ZS)
900
REM CALCULATE THE HEAT LOSS INTO THE INNER
WALL OF THE COMBUSTION CHAMBER.
901
QQ=-CH*HK*RA*6.283185#*(TN(I)-TN(0))/DR
902
TOTQ=TOTQ+QQ*DT
905
X=P*PT
910
IF N<X GOTO 1000 'CHECK IF VALUE OF PT IS
CROSSED AND WHETHER TO PRINT NODE TEMPERATURES
920
QT=N*DT/60 'THE TIME IN MINUTES
925
PRINT #1, USING "####.##"; QT;
930
FOR IZ=O TO S STEP 1
936
PRINT #1, USING "#####."# TN(IZ);
937
NEXT IZ
938
FOR ZI-0 TO ZS STEP 1
939
PRINT #1, USING "#####.#" ;
ZTN(ZI);
940
NEXT ZI
948
PRINT #1,USING "#######.##" QQ;
949
PRINT #1, USING "#########.#" ;
TOTQ
950
P=P+1 'SET P TO PICK OUT NEXT VALUE PT FOR
PRINTING
1000
FOR I=O TO S STEP 1
1010
TT(I)=TN(I) 'SET TEMPERATURES FOR NEXT
ITERATION
1020
NEXT 1
1030
FOR ZI=O TO ZS STEP 1
1032
ZTT(ZI)-ZTN(ZI)
1034
NEXT ZI
1100
NEXT N
1499
BEEP
1500
END
APPENDIX B:
CONVECTION
There are
numerous texts, such as those listed as References (1-5), which
discuss
convective heat transfer in detail.
As described
in Chapter III, convective heat transfer occurs when a liquid
or gas flows,
carrying heat from one point to another followed by conductive
heat transfer
between the newly arrived gas or liquid and the materials
previously
there. Contrast this with conductive
heat transfer which
is due to
direct interaction between individual particles only.
Analyzing
convective
heat transfer is therefore much more difficult than analyzing
conductive
heat transfer because both the motion of the fluid itself and
the energy
transfer processes must be studied simultaneously.
Analysis of
convective heat transfer begins by deriving the continuity,
and the
momentum and energy conservation equations for the fluid.
Due to
the
complexity of the resulting set of equations, they are usually
simplified to
the "boundary layer" equations, so called because the
simplification
is based on the observation that most of the resistance to
heat transfer
between a fluid and a solid is concentrated in a thin
"boundary
layer" next to the solid. The
velocity of the fluid varies
dramatically
across this layer, from zero at the wall to the mainstream
value at its
outer edge. This is shown in Figure
III-7. Within this
boundary
layer, heat transfer is by a complex interaction of heat conduction
and energy
transport by the moving fluid. Once
across this boundary
layer the
heat is rapidly carried away by the solid, or alternatively by
the
mainstream flow of the fluid.
With these
simplifications, <see equations below> for two-dimensional boundary
bsex149.gif (207x600)

layer natural
convective heat transfer become (1-5):
where u and v
are the velocities of the gas in the x and y directions; T
is the
temperature of the gas and p is its density -- [rho][infinity] is the ambient
density; [mu]
is the dynamic viscosity of the gas; k is the conductivity of
the gas; [p]
is the pressure and g is the acceleration due to gravity.
The
geometry is
shown in Figure 1.
bse1x152.gif (437x540)

Boundary
conditions in the case with one bounding
surface are typically:
u(at)
wall)=0 u(at
[infinity])=0
(4a)
v(at)
wall)=0 v(at
[infinity])=0
(4b)
T(at
wall)=[T.sub.wall] T(at
[infinity])=[T.sub.ambient]
(4c)
Initial
conditions are used to set the average initial temperature and
velocity of
the gas entering the region being analyzed.
Even in the
above simplified form, these equations are difficult to solve
and
particularly so in the case of natural convection dominated flows.
In
natural
convection, the case of interest for improved stoves, the force
driving the
flow of the hot gas is its higher temperature and resulting
lower density
compared to its surroundings. In short,
hot air rises. But
as it rises,
it gives up some of its energy to its surroundings, such as
the pot or
stove wall. As its temperature thus
decreases, so does the
force
propelling it upwards. As its velocity
then decreases, so does the
rate at which
it gives up heat to its surroundings, and so on.
It is this
coupled
nature of natural convection flows -- the gas temperature determining
its flow and
heat transfer rates which in turn determine its
temperature
-- that make such systems so difficult to solve analytically
or
numerically. For these reasons,
empirical correlations developed from
experimental
observations are extensively used to analyze and predict the
behavior of
natural convection systems. These will
be discussed before
returning to
analytical and numerical techniques of analysis.
A variety of
parameters and correlations are used regularly in describing
convective
heat transfer. Some of these are listed
in Table 1. Empirical
correlations
for a variety of different situations are listed in Table 2.
Complete
tables of such correlations are given in (9-10).
In improved
stoves, flow regimes of interest include:
o
The plume of hot gas rising from the fire;
o
The stagnation point where the hot gas first
encounters the pot;
o
The wall jet where the hot gas flows
outwards and upwards along the pan
bottom; and
o
The duct flow where the hot gas is channeled
through a narrow gap
between the pot and stove wall before
leaving the stove.
These
different flows are illustrated in Figure 2.
bse2x152.gif (486x486)

The first
three of these, the plume, stagnation point, and wall jet, may
be the basis
for part of the efficiency improvements found in nozzle type
stoves (See
Figure III-8). The fourth, duct flow,
is a primary factor in
the
efficiency improvements found in all three types -- multipot, channel,
and nozzle stoves.
o
For the interested reader, fire plumes are
discussed extensively in
(3,5,11-13,16).
The velocity of the gas in the plume initially increases
with height within the flame but then
decreases slowly above
the flames.
The heat transfer at the stagnation point and along the
pan bottom then increases somewhat with
increasing pot height above the
fire; reaching a maximum just when the
flame tip touches the pot (11).
This partially compensates the reduction in
radiant heat transfer from
the firebed to the pot that occurs with
increasing pot height. Experimentally,
it has been found for channel and multipot
stoves that the
radiative heat transfer is more important
and that better heat transfer
is achieved by placing the pot close to the
fire (17,18). This may,
however, increase dangerous smoke
emissions.
In contrast, nozzle type stoves combine
increasing gas velocity within
the fire plume with reduced stove diameter
(Figure III-8) in order to
sufficiently augment gas velocity and
convective heat transfer on the
pot bottom that it compensates for reduced
radiative heat transfer.
o
Stagnation point heat transfer is discussed
in (3,5,11,12,19). Analytical
solutions have been developed for
nonreacting flows and are found
in most textbooks as well as in Table
1. When combustion is taking
place simultaneously, the situation is
greatly complicated. Dissociated
and intermediate chemical species are
present and have a strong temperature
dependence.
Significant heat transfer can take place due to
diffusion-recombination processes leading
to heat transfer rates much
higher than that predicted in the case of
nonreacting flows (12). The
structure of the flames (turbulent or
laminar, etc.) can also strongly
influence heat transfer rates (19).
Finally, the shape of the pan
bottom influences the heat transfer
somewhat (Table 2).
o
Wall jets, the free flow of hot gas over a
wall with no other bounding
surfaces, are discussed in (1-5,11,14).
Again, analytic solutions are
readily available but must be used with
caution in the present case of
high temperatures, large temperature
differences, and a reacting flow.
In principle at least, adding fins or other
devices to the pan bottom
could also increase the heat transfer.
In practice, such devices would
quickly soot and probably result in lower
overall heat transfer rates.
o
Duct or channel flow heat transfer is
discussed extensively in Chapter
III.
An empirical model for convective heat transfer in multipot
stoves is presented in reference (21) and
gives results generally
similar to those found for channel type
stoves. A simple empirical
model for convective heat transfer in
channel type stoves follows.
Empirical
Analysis of Convective Heat Transfer In Channel Stoves
The
convective heat transfer is given by
Q - hA([T.sub.1]-[T.sub.2])
(4)
where h is
the heat transfer coefficient; A is the surface area of contact
between the
hot gas and the object being heated, and ([T.sub.1]-[T.sub.2] is the
temperature
difference between the hot gas and the object -- in this case
the pot or
stove wall.
The parameter
h is determined either experimentally or, in special cases,
theoretically.
Here the relation
Nu = hG/k
(5)
will be used,
where Nu is the Nusselt number, k is the conductivity of air
and G is the
width of the channel gap through which the hot gas is
flowing.
For low velocity natural convection in a
vertical channel,
reference (8)
uses Nu=1.0. Forced convection heat
transfer results show
Nu=7.541
(3.77 per wall) for fully developed flow between constant
temperature
walls and Nu=4.861 when one wall is perfectly insulated (Table 2).
In the
entrance region of a duct the value of Nu is higher still
(1,2,4,9,10)
but such entrance region effects will be ignored here as the
flow
velocities are low and the channel is narrow ([Re.sub.G]Pr(G)l is small (4).
Now consider
the case of a one pot chimneyless stove as shown in Figure 3.
bse3x152.gif (600x600)

Gas at
temperature [T.sub.a] leaves the fire
and enters the space between the pot
and the stove
wall. This annular space will be
treated as planar in the
model.
The high temperature of the gas and thus low
density give it a
tendency to
rise and a certain pressure is generated.
At the same time,
friction
between the gas and stove wall and pot will counter this tendency
to rise with
a corresponding pressure drop. The gas
velocity will
increase or
decrease till these two competing pressures exactly balance.
In flowing
past the pot and stove walls, a certain amount of heat will be
transferred
from the hot gas -- thus changing the pressure drops, velocities,
and
convective heat transfer, which again changes how much heat is
lost from the
gas, how much its temperature changes, etc.
Consider now
a very small segment of the cylinder, [X.sub.i], with entering gas
temperatures
of [T.sub.h] and exiting gas temperatures of [T.sub.j].
A pressure drop is
generated in
this segment due to friction of the gas with the walls over
the length
[X.sub.i]. Assuming a gas velocity
[U.sub.i] and assuming a kinematic
viscosity
[v.sub.i], and density [[rho].sub.i], which are determined by the average
temperature
in that
segment
[T.sub.i] =
[[T.sub.h]+[T.sub.j]/2
(6)
The pressure
drop is then given by (Table 2 and references 4,9) <see equation 7>
bsetab20.gif (600x600)

bsex153a.gif (77x660)

Corrections
due to entrance region effects will again be ignored for [delta][P.sub.i]
as they were
for the value of the Nusselt number.
This pressure
drop is balanced by the pressure generated due to the
density
difference of the hot gas, [[rho].sub.i], compared to gas at ambient, or
<see equation 8>
bsex153b.gif (69x660)

where g is
the gravitational acceleration, g=9.8 m/[s.sup.2], and [rho][infinity] is the
density of
ambient air.
The heat loss
of the gas to the pot and stove walls is <see equation 9>
bsex153c.gif (165x660)
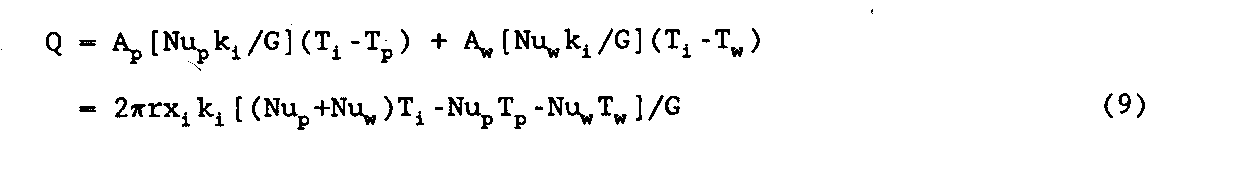
where it has
been assumed that G<<[r.sub.p][perspective to][r.sub.w] [perspective
to]r.
Finally, the
heat lost to the walls per unit time is the same as the heat
lost by the
flowing hot gas which determines its temperature change.
Thus <see equation 10>
bsexx.gif (78x600)
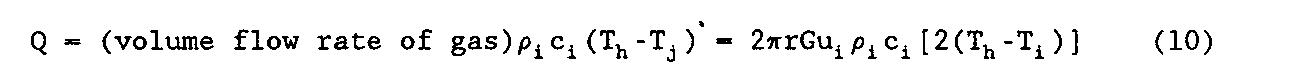
where
[c.sub.i] is the specific heat of the gas at temperature [T.sub.i] in this
section
of the duct.
The unknowns
in the above equations can now be solved for.
Setting the
equations for
pressure drop equal and for heat transfer equal, and using <see equation
below>
bsex154.gif (600x600)

Should one
wish to account for entrance region
effects, the values of
[beta](fRe),
[Nu.sub.p] , and [Nu.sub.w] can be appropriately adjusted.
The thermal
conductivity, k, kinematic viscosity, m, and v, specific heat,
[c.sub.p] of
air are temperature dependent as shown in Table 3.
Fitting an
bsextab3.gif (600x600)

exponential
to this data around T-800K gives <see equation below>
bsex16a.gif (348x660)

Inserting
this into (15) gives <see equation 17>
bsexxvii.gif (181x726)

For a gas
temperature, [T.sub.h], entering a segment [x.sub.i], the average temperature
[T.sub.i] and
hence the exiting temperature [T.sub. ]can now be determined by selecting
the
physically reasonable roots of equation (17).
Determining the heat
transfer for
an entire duct is now simply a process of iterating over each
of the
[x.sub.i] to determine the entrance conditions ([T.sub.h])i+1 for the next
section
[x.sub.i+1]. From these temperatures,
one can calculate the average gas
velocities,
temperatures, heat transfers, etc.,
over the entire length of
the
stove. A useful check on the solution
is that the flow of mass <see equation 18>
bsex18.gif (106x660)

is constant
for the entire length of the duct.
Considerable care must also
be taken to
choose the physically reasonable root [T.sub.i] of equation (17).
The above
model determines the flow rates and heat transfers in the
channel
assuming an initial gas temperature at the channel entrance.
In
turn, the gas
temperature and flow rates determine the combined fire power
and excess
air factor. For example, if it is
assumed that a third of the
energy
released by the fire is in the hot gases as they enter the channel,
the excess
air factor, [lambda], can be determined by solving <see equation 19>
bsex19.gif (104x726)

Here, a third
of the energy released by burning 1 kg of dry wood has been
set equal to
the mass of the hot gases times their specific heat and
temperature
above ambient. The factor 5 comes from
the volume of air
needed for
stoichiometric combustion with 1 kg of wood.
With the calculated
flow rates
and the above excess air factor, the fire power is <see equation below>
bsex20.gif (118x660)

A simple
computer program that solves this system is attached and the
output data
is shown in the text (see note 20). Due
to the lack of
precision in
the correlations used and to the excessive simplification of
the model
itself, there tend to be some deviations from the requirement
that the mass
flow be constant, particularly for very narrow channels
where the
heat transfer is most abrupt. These
variations are usually less
than
10%. For very narrow channels,
typically 3 mm or less, there are
also often
problems in finding the physically reasonable roots [T.sub.i] of
equation
(17). Finally, these same
simplifications and approximations
caused the
model to approach the efficiency limit suddenly rather than
asymptotically
(Figure III-9A). Practically, these are
of little interest.
The baseline
parameters for this model were [Nu.sub.p]=4.86; [Nu.sub.w]=0; fRe=24; and
[T.sub.g]
=900 K and output for these parameters is shown in Chapter III.
That
the model is
generally robust was verified by varying convective heat
transfer
coefficients for the pot and the wall, inlet gas temperatures,
numerical
step size, and a variety of other factors.
In all cases the
behavior of
the model remained generally the same.
For example, changing
the Nusselt
number for the pot from 1.0 to 8.0 had essentially no effect
on the form
of the curve, e.g. , Figure III-9A, but the channel gap for a
50% channel
efficiency varied from 4.3 mm ([Nu.sub.p]=1) to 7.2 mm ([Nu.sub.p]=8).
Both of these
are quite close to the channel gap of 6.4 mm for the case of
[Nu.sub.]p=4.86
(L=5 cm, [T.sub.g]=900 K). Similarly,
increasing the inlet gas temperature
from 700 K to
1300 K did not change the general shape of the curve
(Figure
III-9A); but only shifted its position.
For example, the channel
gap for 50%
channel efficiency changed from 7.0 mm (700 K) to 8.9 mm (1300
K) for a 10
cm long channel.
The above
model assumes a constant channel gap.
In practice, the pot will
not be
perfectly centered nor the stove perfectly round.
As discussed in
Chapter III,
this can strongly reduce the heat transfer as the slightly
wider
sections tend to lose very large amounts of heat.
The reason for
this is the
large variation in pressure drop with channel gap (equation
7).
A wedge of the duct with a slightly larger
gap will suffer much
smaller
pressure drops, 1/[G.sup.2], so that the hot gases will flow out of the
stove much
easier at that point. Table 4 lists
these points in detail.
bsextab4.gif (600x600)

A related
calculation has been done for the convective heat transfer to
the second
and subsequent pots of a multipot stove and is described in
detail in
(21). In general, however, multipot
designs are not recommended
even when
their total thermal efficiency is high because it is very
difficult to
effectively control the heat input to each of the pots
individually
from one fire.
Although the
above empirical model is useful in describing the expected
trends in the
performance of the duct with dimensional changes, gas
temperatures,
and other factors, it is not expected to be an accurate
predictor of
performance. To more accurately do
that, numerical analysis
of the
boundary layer equations (1-3) is necessary.
References (3,22-25)
are
particularly useful reviews of this.
For low
temperature differences, the Boussinesq approximation, which sets
[rho],
[micro], k, and [c.sub.p] constant everywhere except the term
g([rho][infinity][lambda]-[rho]) is used.
Numerical
solutions in this case for particular geometries are given by
(26-27), and
with time dependence by (33). For
improved stoves, temperature
differences
of several hundred degrees are found over distances of a
few
millimeters. Under these conditions,
the Boussinesq approximation is
less accurate
(6) and other techniques are necessary, as described in
(3,14,28-29).
In addition,
flows in improved stoves are driven by buoyancy forces which
presents
additional difficulties in obtaining stable numerical solutions.
Various
techniques used to handle these difficulties are described in
references
(3,23-25,28,30-32).
In
particular, for duct flows only the duct geometry is known and the
pressure in
equation (2) above is a variable. This
requires an addition
to equations
(1-3) for there to be a solution and is usually done by
requiring the
mass flow in the duct to be constant (3). <see equation 21>
bsexe21.gif (102x798)

References
(26-27) then solve the system of difference equations generated
from
equations (2,3,21) and use the results in equation (1) to determine
the velocity
v. Such a procedure is not fully self
consistent. In
contrast,
references (3,31-32) solve equations (1-3) and vary p iteratively
until
equation (21) is satisfied. For the
interested reader,
detailed
computer programs solving these equations are given in (3).
Finally, it
is useful to note from the above analysis that there are a
number of
"scale" factors which enter into stove design.
Some of these
are listed in
Table 5. As an example, consider what
happens when a stove
and pot and
all the associated dimensions are changed in scale by a factor
of two --
that is, they are all doubled (or halved) in size.
In that case,
the energy
needed to heat the pot increases by its volume or [D.sup.3]=[2.sup.3]=8 times
where D is
the pot diameter, but the energy available from the fire only
increases by
its surface area or [D.sup.2]=4 times.
This is a result of the heat
required
being determined by the volume of the pot while the heat supplied
is determined
roughly by the area of the fire. The
effect on various other
aspects of
stove performance can be similarly estimated from Table 5.
TABLE 1
Correlations,
Definitions, and Parameters in Convective Heat Transfer
Characteristic
length--the primary dimension determining system behavior:
For a flowing fluid bounded on only one
side, the characteristic length
of the system would be the distance from
the leading edge of the
bounding wall; for flow between two walls
it would be the distance
between them; and for flow in a pipe it
would be the inner diameter.
Developed
flow: When the fluid first enters the
duct, there are rapidly
changing fluid velocities very close to the
duct wall, and a relatively
constant unperturbed flow velocity at the
center of the duct. This is
known as the entrance region and heat
transfer coefficients are somewhat
higher than further downstream.
With distance into the duct, these
surface boundary layers of fluid (with
rapidly changing velocity
according to the distance from the duct
wall) grow thicker until they
merge at the center of the duct.
That is, the flow across the entire
duct has been perturbed by the friction
with the wall. This point on
is known as the developed region.
In this region the flow velocity has
a parabolic profile.
More precisely, a duct flow is said to be
fully
developed when the relative flow velocities
across the channel width
are no longer changing along the length of
the duct.
Grashof
number, Gr: Gr-g[beta]([T.sub.w]-[T.sub.[infinity])[x.sup.3]/[v.sup.2] where g
is the acceleration due
to gravity, [T.sub.w] is the wall
temperature, and [T.sub.[infinity] is the fluid temperature
far from the wall, and x is the
characteristic dimension of the system.
Gr gives the magnitude of the buoyant force
relative to the viscous
force.
Buoyant forces are generally only important in natural convection
flows.
Ideal Gas
Law: PV-nRT where P is the pressure, V is the volume, and T is
the-temperature of n, moles of the gas. R
is the universal gas constant
R=8.314 J/[degrees]Kmole.
Kinematic
Viscosity, v: v=[mu]/[rho] where [rho] is the fluid density. v gives the
rate at which momentum diffuses through a
fluid due to molecular motion
Laminar
flow: A flow is termed laminar when its
layers of flow, or
streamlines, are smooth, even, well
ordered, etc. This condition
normally occurs for relatively low fluid
velocities.
Newtonian
Fluid: [tau]=[mu]u(du/dy) by definition of a newtonian fluid where [tau] is
the shear stress or force per unit area on
a bounding fluid layer or
surface and is in the direction of fluid
flow; u is the velocity in the
direction of fluid flow, x, Figure 1; and
[mu] is the dynamic viscosity.
Nusselt
number, Nu: Nu(x)=[h.sub.x]/k where [h.sub.x] is the local convective heat
transfer coefficient, x is the
characteristic length of the system, and
k is the thermal conductivity of the
fluid. Because h is approximately
given by k/[delta] where [delta] is the
thickness of the local thermal boundary
layer, the Nusselt number is x/[delta] or
the ratio of the characteristic
length of the system to the local thermal
boundary layer thickness.
Peclet
number, Pe: Pe-RePr The Peclet number
is a measure of the
relative importance of convection versus
conduction mechanisms within
the fluid.
Prandtl
number, Pr: Pr=v/[alpha] Pr is a
measure of the fluid's ability to
diffuse momentum, v, compared to its
ability to diffuse heat, [alpha]. For
gases, the Prandtl number is nearly
constant with temperature and is
about .68 for air.
Rayleigh
number, Ra: Ra=GrPr
Reynolds
number, Re(x): Re(x)=[u.sub.[infinity]x/v] where [u.sub.[infinity] is the free
stream velocity
of the fluid and x is the characteristic
length of the system. The
Reynolds number is the ratio of inertial
forces in the fluid to the
viscous forces.
The transition from laminar to turbulent flow is
described by a critical value of
Re(x). For flow along a single wall
this critical value is typically
Re=5x[10.sup.5]; for flow in a pipe it is
typically Re-2300.
Stanton
number, St:
St=h/[[rho]c.sub.p][u.sub.[infinity]=[Nu/Pe gives the ratio of convected
heat
transfer to that virtually transferable if
temperatures were equalized.
Thermal
Diffusivity, [alpha]: [alpha]-k/[rho]c
where k is the thermal conductivity, [rho] is
the density, and c is the specific heat of
the fluid. [alpha] gives the rate
at which heat can diffuse through a
substance.
Turbulent
flow: A flow is termed turbulent when
its streamlines are
randomly intermixed and disordered.
This condition normally occurs for
relatively higher fluid velocities.
Volume
Coefficient of Expansion, <see equation>
bsex158.gif (135x230)

For ideal
gases [beta]=1/T.
TABLE 5
Some Scale Factors in
Stove Design
Pot diameter/fire diameter
D/D
Pot to stove wall channel
gap/length G/L
FACTOR
SCALES AS
Energy needed to heat a pot to
boiling [D.sup.3]
Energy rate available from the
fire [D.sup.2]
Maximum fire size (limited by gas
escape) D
Heat transfer within channel
DL/G
Pressure drop in channel
L/[G.sup.3]
COMPUTER
PROGRAM FOR EMPIRICAL MODEL OF CONVECTIVE HEAT TRANSFER
5 CLS :BEEP
10 CLEAR
15 OPEN
"LPT1:" FOR OUTPUT AS #1
16 PRINT
"ALL UNITS ARE IN KILOGRAMS, METERS, SECONDS, DEGREES KELVIN AND
WATTS"
17 INPUT
"ENTER CHANNEL LENGTH, L, AND WIDTH, LL"; L, LL
20 S=200*L
25 DIM QQ(S),
VV(S), TT(S)
30 INPUT
"ENTER GAS TEMPERATURE, TG"; TG
110 D=.3
`diameter of pot
112 TW=373 :
TP=373 : TA=300 `temperatures of wall, pot, and ambient
115 REM SET
NUSSELT NUMBERS AND FRICTION FACTOR AS DESIRED
120 NUP=4.86
: NUW=O! : FR=24! `NUW=O corresponds to a perfectly insulated wall
130 DA=1.1774
`ambient air density
200 TB=TG
'sets temperature at bottom of first segment equal to entering gas temperature
300 XI=L/S
`length of segment
310
B=39.2*DA*LL'4/(FR*XI)
400 FOR J=1
TO S STEP 1
500 Y=10
`increments temperature by 10 degrees in search for root
510 T1=TB
520
F1=1.78E-15*(NUP+NUW)*T1'4.2-1.78E-15*(NUP*TP+NUW*TW)*T1'3.2+B*T1'2-B*<TB+TA)*T1+B*TB*TA
600 FOR 1=1
TO 60 STEP 1
610 T2=T1-Y*I
620
F2=1.78E-15*(NUP+NUW)*T2'4.2-1.78E-15*(NUP*TP+NUW*TW)*T2'3.2+B*T2'2-B*(TB+TA)*T2+B*TB*TA
640 G=F1*F2
650 IF
G<=0 GOTO 700 'check to see if have crossed root, F=0, between F1 and F2
660 F1=F2
'sets up for next check to determine crossover
670 NEXT 1
700 IF
Y<=1 GOTO 750
710 Y=1
'iterates by one degree increments
720 T1=T2+10
'raises temperature to that at crossover of root
730 GOTO 520
750
T2=T2+ABS(F2)/(ABS(F1)+ABS(F2)) 'linear interpolation of T2 root from function
values
810
VI=.0000823*(T2/800)'1.626
820
KI=.05779*(T2/800)'.746
900
QI=3.14*D*XI*KI*NUP*(T2-TP)/LL 'average heat flux in section
910
UI=19.6*LL'2*(T2-TA)/(FR*VI*TA) 'average velocity in section
1000 QQ(J)=QI
: VV(J)=UI : TT(J)=T2
1100
TB=2*T2-TB 'calculates temperature at top of current section and bottom of next
section
1200 NEXT J
1290 SQ=O :
SM=O
1400 PRINT
#1, "L="; L, "LL="; LL, "D="; D
1410 PRINT
#1, "TG="; TG, "NUP="; NUP, "NUW="; NUW,
"FR="; FR
1450 REM
PRINT #1, " TEMP " ; "
HEAT "; "
VEL
"; " MASS "
1500 FOR IP=1
TO S STEP 1
1510
MF=3.14*D*LL*VV(IP)*DA*TA/TT(IP) 'mass flow in each section
1520 GOTO 1530
'this bypasses the step by step printout
1521 PRINT
#1, USING "#######.##"; TT(IP);
1522 PRINT
#1, USING "######.###"; QQ(IP);
1523 PRINT
#1, USING "#####.####"; VV(IP);
1524 PRINT
#1, USING "####.######"; MF
1530
SQ=SQ+QQ(IP) 'sum of heat fluxes in each section
1535 SW=SM+MF
'sum of mass flow in each section
1540 NEXT IP
1545 MFA=SM/S
'average mass flow rate
1550
CG=1097.8*(TG/800)'.176 'specific heat of gas entering channel
1555
XSR=.17*(6000000!/(CG*(TG-TA))-1) 'excess air if .33 fire energy in hot gases
entering channel
1560
PF=18000*MFA/(1+5.885*XSR) 'total fire power for average flow rate and assumed
excess air factor
1561
PFQ=MFA*CG*<TG-TA) 'total energy of gases in channel based on average flow
rate
1565
EFT=(TG-TT(S))/(TG-TA) 'efficiency based on temperature change of gas
1570
EFG=SQ/PFQ 'heat flux to pot obtained by adding the Q=hAdT of each segment
1575 MFA=SM/S
'average gas flow rate
1580
SQT=EFT*PFQ 'heat flux to pot (nuw=0) based on temperature change in gas
1601 PRINT
#1, "PF=";
1602 PRINT #1,
USING "###,####"; PF;
1603 PRINT
#1, " EFT=";
1604 PRINT
#1, USING "#. #####"; EFT;
1605 PRINT
#1, " EFQ";
1606 PRINT
#1, USING "#.#####"; EFQ;
1607 PRINT
#1, " QF=";
1608 PRINT
#1, USING "#####.####"; SQ;
1609 PRINT
#1, " MFA=";
1610 PRINT
#1, USING "##.#######"; MFA
1620 PRINT
#1, "PFQ=";
1621 PRINT
#1, USING "######.###"; PFQ;
1622 PRINT
#1, " QFT=";
1623 PRINT
#1, USING "#####.####"; SQT
1700 BEEP
1800 END
APPENDIX
C: RADIATION
All
substances continuously emit electromagnetic radiation due to the
molecular and
atomic motion associated with the internal energy of the
material. In
the equilibrium state, this internal energy is proportional
to the
temperature of the substance. Basic texts that discuss radiation
and radiation
heat transfer in detail are listed as references (1-3).
For
electromagnetic radiation in a vacuum, the wavelength and frequency
are related
by the equation <see equation 1>
bsexe1.gif (92x798)

where c is
the speed of light, c=2.998x[10.sup.8] m/s. Figure 1 relates the
bse1x168.gif (600x600)

various bands
of radiation to their wavelength. The energy in a single
photon of
radiation is related to its frequency by the equation <see equation 2>
bsexe2.gif (90x877)

where h is
Planck's constant, h=6.6256x[10.sup.-34] Js.
The ability
of an object to emit radiation is given by its emissivity [epsilon]
and is
usually a function of the wavelength of the radiation. Table 1
lists the
average (frequency independent) emissivities for a variety of
common
materials. Similarly, the ability of an object to absorb radiation
is usually
wavelength dependent and is given by [alpha]([lambda]). The emissivity and
absorptivity
of a material are equal, [alpha]([lambda])= [epsilon]([lambda]).
Objects that
are perfect absorbers (emitters), [alpha]-1.0, of radiation
regardless of
wavelength are known as blackbodies. If they only absorb a
fraction
0<[alpha]<1.0 of the impinging radiation they are known as graybodies.
Perfect
reflectors have [alpha]=0.0.
For a black
body, heat energy is radiated at a rate given by the Stefan-Boltzmann
law <see
equation 3>
bsexe3.gif (93x726)

where [sigma]
is the Stefan-Boltzmann constant, [sigma]=5.6697x[10.sup.-8] W/[m.sup.2]
[K.sup.4], A is the
emitting area
of the object in square meters, and T its temperature in
degrees
Kelvin. This emitted radiation has a
maximum intensity at the
wavelength
given by Wien's law <see equation 4>
bsexe4.gif (92x798)

For
graybodies, the Stefan-Boltzmann law is modified as <see equation 5>
bsexe5.gif (92x798)

As can be
seen, the total energy radiated by a black body (or gray body)
is strongly
temperature dependent. Increasing the
temperature just 10
percent
increases the heat output by [(1.1).sup.4] or nearly 50 percent.
TABLE 1
Emittance
[epsilon] [perpendicular to] In The Direction Of The Surface Normal
Material
[degrees]C
[epsilon] [perpendicular to]
Metals:
Aluminum,
bright rolled 170
.039
, paint
100
.2-.4
, oxidized at 600[degrees]C
300
.13
Chrome,
polished
150
.058
Iron, bright
etched 150
.128
, bright abrased
20
.24
, red rusted
20
.61
, hot rolled
20
.77
" "
130
.60
, heavily crusted
20
.85
, heat resistant oxidized
80
.613
Nickel,
bright matte
100 .041
Stainless
steel 301
260
.18
Stainless
steel 347, oxidized
at 1100[degrees]C
300
.87
Tin, bright
tinned iron sheet 38
.08
Paints:
White
100
.925
Black matte
80
.970
Pigments:
Lampblack
52
.94
Candle soot
52
.95
Red ([Fe.sub.2][O.sub.3])
52
.96
Miscellaneous:
Brick, mortar, plaster
20
.93
Concrete
30
.94
Fired clay
67
.91
Refractory
brick, ordinary
1100 .59
white
1100
.29
dark chrome
1100
.98
Sand
25
.90
References (1,2)
At the same
time that an object is emitting radiant energy it is also
absorbing
energy emitted by other objects. A "view factor" [F.sub.12] can then
be defined as
the fraction of total energy radiated by surface 1 which is
intercepted
by surface 2.
In the
simplest case of a point source radiating spherically outwards, a
small section
of a surrounding spherical shell will intercept a fraction
([A.sub.2]/4[pi][r.sup.2])
of the energy radiated by this source (Figure 2). Thus, in this
bse2x168.gif (486x486)

case,
[F.sub.12=A.sub.2/4[pi]r.sup.2] and the heat from point 1 arriving at
surface 2 is
<see equation 6>
bsexe6.gif (116x726)

where
[epsilon][sub. perpendicular to], is the emissivity at right angles (normal) to
the surface.
It should be
noted that this heat transfer is very sensitive to the
distance
between the two; doubling the distance r reduces the heat
transfer by
four times.
In the more
general case, the radiant heat transfer must be calculated by
integrating
the "view" one surface element has of the other over both
entire
surfaces. With the parameters as defined in Figure 3, <see equation 7>
bse3x168.gif (540x540)
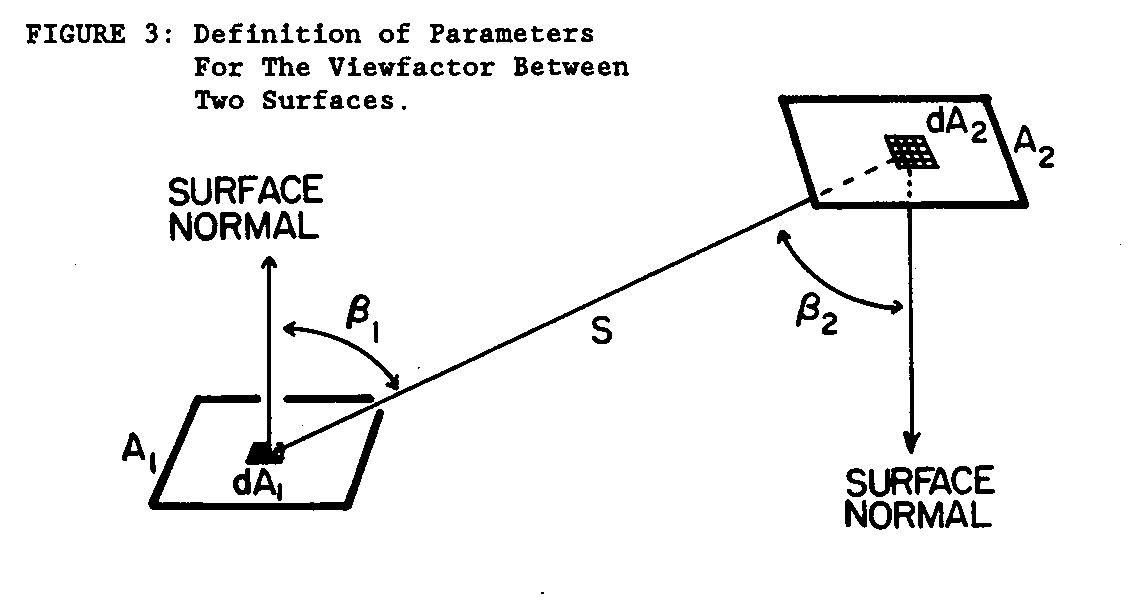
bsexe7.gif (116x726)

For the case
of two flat disks facing each other on the same axis, Figure 4,
bse4x172.gif (437x437)

this integral
gives <see equation 8>
bsexe8.gif (129x726)

Graphs of
this function are given in Chapter III. The view factors for
other
particular geometries are given in references (1-4).
From the
definition of the view factor as the fraction of the total energy
radiated by
surface 1 which is intercepted by surface 2, an enclosed
surface i
gives the identity <see equation 9>
bsexe9.gif (127x798)

where the
surfaces k are all the other surfaces which enclose surface i.
The net
radiant heat lost or gained by surface i is the difference between
the heat it
radiates and that which it absorbs from other radiating
surfaces.
Thus, for blackbodies (see equation 10>
bsexe10.gif (129x726)

Finally, by
symmetry there is the relation between surface i and surface k
<see
equation 11>
bsexe11.gif (129x726)

With these
equations the radiant transfer for a variety of simple geometries
can be
determined. Consider, for example, the heat balance on the
inner surface
of the cylindrical combustion chamber shown in Figure 5. As
bse5x172.gif (486x486)

the wall
itself intercepts much of the heat it radiates, its net heat gain
must be
written as the difference between that which the wall radiates
specifically
to the pot and fire and that which is radiated by the pot and
fire to the
wall. It is assumed that the surfaces are all perfect
absorbers,
[epsilon]=1. For the interior of a woodburning stove this is a good
approximation
as the walls and pot will be heavily sooted. Thus, <see equation 12>
bsexe12.gif (116x726)

Using
equation (11) and noting that symmetry gives [A.sub.f][F.sub.fw] =
[A.sub.p][F.sub.pw], this
simplifies to
<see equation 13>
bsexe13.gif (127x798)

Finally, by
equation (9) <see equation 14>
bsexe14.gif (104x726)

and
[F.sub.fp] is given by equation (8). The results of calculations based on
equations
(3,5,8,13,14) and the wall temperatures as determined by the
model
developed in Appendix A are presented in figure 6. As seen, well
bse6x172.gif (600x600)

insulated
walls can substantially increase radiant heating of the pot.
In the more
general case [epsilon][not equal to]1 and multiple reflections between the
different
surfaces must
be considered.
For the
interested reader there are numerous additional factors in radiant
heat transfer
from fires worthy of consideration. Although the radiation
from the
flames is a small portion of the total energy released by the
fire,
typically less than about 14% (5), it plays a crucial role in the
combustion
process itself. Radiant energy from the flames heats the wood
and releases
more volatiles that burn in the flame, maintaining the
combustion
and controlling, in part, its rate.
To understand
the emissivity of a flame requires knowledge of the luminous
(yellow)
emissions of the burning soot which acts as a cloud of miniscule
blackbodies
as well as of the infrared molecular band emissions of the
combustion
products, primarily [CO.sub. 2] and [H.sub.2]O. Reference (6) calculates the
detailed
extinction and scattering coefficients for a cloud of soot
particles.
Reference (7) develops approximate techniques for calculating
the total
flame emissivity including the black body spectrum of soot, the
molecular
band emission of the gases, and, additionally, the overlapping
and
interactions of the bands themselves. Reference (8) details the
importance of
flame dimensions on the relative magnitudes of soot versus
molecular
band emissions. Reference (9) presents
experimental results
which show
that the presence of water vapor in a flame in addition to that
generated by
the combustion itself can greatly reduce the emission of the
soot
particles and the total flame emissivity. This may be a dominant
factor in
controlling the burning rate of wet fuel. An excellent review
of flame
radiation is given by reference (10).
In addition
to the above complexities of strongly wavelength dependent
emissivities,
the calculation of radiant heat transfer is also complicated
by the
transfer of energy taking place between widely separated elements.
This is to be
contrasted with the case of conduction and convection for
which it is
adequate to consider only adjacent volume elements. As a
consequence,
a complete description of radiant heat transfer requires the
solution of
systems of nonlinear integrodifferential equations. Reference
(2) discusses
the formulation of such systems of equations and presents a
few case
studies. References (11-13) present additional examples of this
type of
analysis.
APPENDIX D:
COMBUSTION
In this
appendix various chemical and physical properties of biomass and
its
combustion will be discussed in somewhat more detail than was possible
in the
text. Due to the complexity of the
subject, however, extensive
references will
be given for further reading rather than attempting to
provide an
exhaustive review here. The topics
discussed below include:
chemical and
physical properties of biomass and its chars, the pyrolysis
of wood, the
combustion of charcoal, diffusion flames, soot and air
quality.
Chemical and
Physical Properties of Biomass and Biomass Chars
As mentioned
in the text, there are a variety of ways to characterize the
chemical and
physical properties of biomass and its chars.
These include
the
following:
Proximate
analysis of biomass lists the fractions of biomass in terms of
moisture,
volatiles, fixed carbon, and ash. Such
analysis is usually
performed by
slowly heating the material to 950[degrees]C in an inert atmosphere
and examining
the material released as a function of temperature.
Table 1
lists typical
values from proximate analysis for raw biomass.
Table 2
shows the
effect of pyrolysis temperature on the final char yield (3).
Ultimate
analysis determines the elemental composition of the material.
Beginning
with catalytic combustion or pyrolysis, biomass is broken down
into carbon
dioxide, water, hydrogen sulfide, and nitrogen.
These gases
are then
measured by gas chromatography using flame ionization or thermal
conductivity
detectors (1). Typical values are
listed in Tables 3 and 8
below.
To convert the values in Table 3 into molar
ratios, the weight-percent
must be
divided by their respective atomic weights given in Table 4.
Results are
shown in Table 5. From this, the amount
of oxygen needed
to completely
burn the material, assuming perfect mixing or in other words
the
stoichiometric ratio of oxygen, can be calculated as shown in Table 6.
For charcoal,
8.3 [m.sup.3] of air are needed to burn 1 kg; for wood, 5.5
[m.sup.3] air
are needed
per kilogram.
The ash
remaining following combustion is typically composed of CaO, [K.sub.2]O,
[Na.sub.2]O,
MgO, SiO, [Fe.sub.2][O.sub.3], [P.sub.2][O.sub.5], and [SO.sub.3]. CaO
generally represents about half
the ash and
[K.sub.2]O is about 20 percent (1). The
potassium carbonate, in
particular,
is useful in making soap.
Calorific
values were briefly mentioned in the text and more extensive
lists are
given in Tables 2, 7 and 8 and in references (3-7).
The
calorific
value can also be estimated from the results of ultimate
analysis
using standard correlations available in the literature and have
errors of
typically less than 2 percent. However,
it is generally easier
to perform
bomb calorimetry measurements and determine the calorific value
of biomass
directly rather than circuitously do ultimate analysis followed
by the use of
such correlations.
The density
of wood is determined by the numbers and sizes of the pores
within it and
can vary dramatically as seen in Table 9 (1,8).
Wood, and
biomass
generally, consists of long fibers of cellulose
([C.sub.6][H.sub.10][O.sub.5]).sub.m] and
hemicellulose
([C.SUB.5][H.SUB.8][O.sub.4]).sub.n] cemented together by lignin
([C.sub.9][H.sub.10][O.sub.3]([CH.sub.3]O)[sub.9-1.7)p]
For both hard
and softwoods, cellulose is about 43 percent of the total.
Hemicellulose,
however, forms about 35 percent of the typical hardwood
compared to
28 percent of softwood while lignin is about 22 percent of
hardwood and
29 percent of softwood (1). Calorific
values for each of
these components
are given in the text.
Because woods
consist of these long fibers running lengthwise, their
properties
are highly anisotropic. Their
permeability, for example, can
be 10,000
times (and more) greater in the longitudinal direction than in
the transverse
(1,9). This is important because the
permeability controls
TABLE 1
Proximate Analysis of Raw
Biomass
Material
Volatiles(*)
Fixed Carbon(*)
Ash(*) Reference
Oven Dry Woods
Western Hemlock
84.8%
15.0% 0.2%
1
Douglas Fir
86.2
13.7 0.1
1
Ponderosa Pine
87.0
12.8 0.2
1
Redwood
83.5
16.1
0.4 1
Cedar
77.0
21.0 2.0
1
Oven Dry
Barks
Western Hemlock
74.3
24.0 1.7
1
Douglas Fir
70.6
27.2
2.2 1
Ponderosa Pine
73.4
25.9 0.7
1
Redwood
71.3
27.9 0.8
1
Cedar
86.7
13.1 0.2
1
Oven Dry
Bagasse 85.7
11.5
2.8 2
(*) weight
percent, dry basis; Reference (1)
TABLE 2
Australian Eucalyptus Retort
Charcoal
Charcoal
Temperature
Yield %
Approximate
Volatile Ash by
Calorific
of
by Weight
Fixed Matter
Weight
Value
Carbonizing
of Dry
Carbon, by by
Weight %
MJ/kg
[degrees]C
Wood Sample Weight
% %
400
40
78 21.5
0.5
31.5
450
35
82 17.5
0.5
33.1
550
31.5
88.5 11.0
0.5
33.9
650
28
95 4.5
0.5
34.7
Reference
(56)
the movement
of water vapor and volatiles away from the combustion zone
out of the
wood or into cooler parts of it.
Materials such as biomass
briquettes or
sawdust may burn with greater difficulty than wood because
their long
fibrous nature is disrupted and air pockets within the material
insulate and
localize the combustion zone (57).
Similarly, thermal
conductivities
of wood are about twice as big in the longitudinal direction
as in the
transverse (8). Representative values
are listed in Table 9.
Additionally,
these properties vary with the moisture content in fresh
biomass and
degree of charring in burning biomass.
Even the growth rings
and grain
structure can strongly affect the combustion characteristics of
wood
(10-12). Much more detailed discussions
of the physical and chemical
structure of
biomass and biomass chars can be found in references (1,8).
TABLE 3
Ultimate Analysis of
Biomass
Material
C(*)
H(*) N(*)
S(*)
O(**) Ash
Charcoal
80.3%
3.1% 0.2%
0.0%
11.3% 3.4%
Douglas
Fir 52.3
6.3 0.1
0.0
40.5 0.8
" "
" " Bark 56.2
5.9
0.0 0.0
36.7
1.2
Hickory
49.7
6.5 0.0
0.0
43.1 0.7
Rice
Hulls 38.5
5.7
0.5 0.0
39.8
15.5
Rice
Straw 39.2
5.1
0.6 0.6
35.8
19.2
Animal
Waste 42.7
5.5
2.4 0.3
31.3
17.8
(*) Weight
percent, dry basis; (**) By difference;
Reference (1)
TABLE 4
Atomic Weights
Element
C
H (H2)(*) N
(N2) S
O (02)
Atomic
weight 12.0
1.0 14.0
32.0
16.0
(*) The form
in parentheses is the molecular form in which the chemical
species is normally found in air at
atmospheric pressure and 20[degrees]C.
TABLE 5
kmoles of element/kg of
biomass
Material
C
H N
S
O
Charcoal
.0669(*)
.031 .00014
0.0-
.0071
Douglas
Fir .0436
.063 .00007
0.0-
.025
Animal
Waste .0356
.055
.002 0.0001
.020
(*)
Calculated by dividing values in Table 3 (fractional basis) by respective
atomic
weights, Table 4.
TABLE 6
Stoichiometric
Amounts of Oxygen Needed for Combustion per Kg Biomass(*)
Material
C[right arrow][CO.sub.2]
H[right arrow]H.sub.2]0 less 0
in Total 0 Needed
Air Volume
biomass (kmoles)
([m.sup.3])(**)
Charcoal
.134
.015
.0071
.142 8.3
Douglas
Fir .087
.032
.025
.094
5.5
Animal
Waste .071
.028
.020
.079 4.6
(*) Based on
molar values from Table 5
(**) Air is
78 percent [N.sub.2] and 21 percent [O.sub.2]. At 27 C and sea level
pressure, the density of air is about
1.177 kg/[m.sup.3] and air thus
has about 8.6 moles [O.sub.2] per
[m.sup.3].
TABLE 7
Calorific Values
Material
Gross Calorific Value
Reference
Hardwood
Average 19.734 [- or +]
0.981 MJ/kg
4
Hardwood
Bark 19.343 [- or +]
1.692 4
Hardwood
Sapwood 20.349 [- or +]
0.791 4
Hardwood
Heartwood 20.683 [- or +]
0.961 4
Softwood
Average 20.817 [- or +]
1.479
4
Softwood
Bark 21.353 [- or +]
1.221 4
Rice
Straw 15.21
1
Rice
Hulls 15.37
1
Dung
Cakes 17.17
1
Corn
Cobs 18.9
5
Coconut
Shells 20.1
5
Coconut
Husks 18.1
5
Cotton
Stalks
15.8
5
Alfalfa
Straw 18.4
5
Barley
Straw 17.3
5
Charcoal
Table 2
Material
Gross Calorific Value(*)
Density(*)
n-Butane
45.72 Mj/kg
548 kg/[m.sup.3]
Diesel:
light 42.37
876
medium
41.87
920
heavy
41.37
960
Ethanol
26.80
789
Gasoline (73
Octane) 44.13
720
Kerosene
43.12
825
Methane
50.03
- - -
Methanol
19.85
793
Propane
46.35
508
(*) Reference
(13)
Because of
the various complications it is extremely difficult to model
realistically
the combustion of wood. Thus, the
following will only
present very
simple models of particular aspects of wood combustion and
then
extensively reference the literature for more detailed investigations
by the
interested reader. As background, general
texts on combustion are
listed as
references (13-16).
TABLE 8
Ultimate Analysis and Calorific Values
For Biomass Chars
Material
C
H N
S
O Ash
Calorific
Redwood
Charcoal
Value MJ/kg
(pyrolized at 550 C)
75.6
3.3 0.2
0.2
18.4 2.3
28.8
Redwood
Charcoal
(pyrolized at 940 C)
78.8
3.5 0.2
0.2
13.2 4.1
30.5
Oak Charcoal
(pyrolized at 570 C)
64.6
2.1
0.4 0.1
15.5
17.3 23.0
Fir Bark
Char 49.9
4.0
0.1 0.1
24.5
21.4 19.2
Rice Hull
Char 36.0
2.6
0.4 0.1
11.7
49.2 14.2
Grass Straw
Char 51.0
3.7
0.5 0.8
19.7
24.3 19.3
Animal Waste
Char
34.5 2.2
1.9
0.9 7.9
48.8
12.7
Reference (1)
TABLE 9
Densities,
Conductivities, and Thermal Diffusivities For Various Woods
Thermal Thermal
Conductivity
Conductivity Diffusivity
Diffusivity
Density
Transverse
Longitudinal Transverse
Longitudinal
Wood
kg/[m.sup.3]
W/mC
W/mC
[m.sup.2]/s [m.sup.2]/s
Fir
540
0.14
0.34
18.7X[10.sup.8]
45.9X[10.sup.8]
Mahogany
700
0.16
0.31 16.6
32.3
Oak
820
0.21
0.36 18.7
32.1
White
Pine 450
0.11
0.26 17.8
42.1
Teak
640
0.18
0.38 20.1
43.5
Reference (8)
Wood
Pyrolysis <see figure 1>
bse1x184.gif (486x486)

Wood
pyrolysis was described qualitatively in Chapter III.
Briefly, as
wood is
heated it undergoes chemical reactions in which volatile gases are
evolved and
escape the wood, leaving a porous char behind.
Among the
earliest
quantitative models to describe this phenomena was that of
reference
(17). Other, more recent and more
complete models are listed as
references
(18-26).
The typical
model is based on the transient heat conduction equation,
equation
(A-1), to account for heat being conducted into the wood.
Additional
terms are added to account for the heat carried out of the wood
by the
escaping volatiles and to account for the energy absorbed or
released by
the pyrolysis reaction itself. Other
constraints include
accounting
for the decomposition process and for the change in the thermal
conductivity,
density, specific heat and any other relevant properties of
the wood/char
as the decomposition process progresses.
The form of
the pyrolysis equations in one dimension is then: <see equation below>
bsex180.gif (313x660)

In equation
(1), the first two terms [delta]([[rho].sub.s][c.sub.s]T)/[delta]t=[delta]{[delta]T/[delta]x)}/[delta]x
is simply
the equation
for transient heat conduction, equation (A-1), for materials
with variable
thermophysical properties. The
variables [[rho].sub.s],[c.sub.s],k, and T
are the
density, specific heat, thermal conductivity, and temperature of
the
pyrolyzing solid, i.e. the charring wood.
The third term [delta]([[rho].sub.g][V.sub.g][C.sub.g]T)/[delta]x
is the heat
carried out of the pyrolyzing solid by the volatile gases of
density
[[rho].sub.g] moving with a velocity [V.sub.g] and having a specific heat
[C.sub..g]. Extensive
data on the
magnitude of internal convection is given in reference
(19).
It is assumed that the gases are in thermal
equilibrium with the
solid.
The final term of equation (1), [Q.sub.p][delta][[rho].sub.s]/[delta]t
, is the energy absorbed
(or released)
by the pyrolysis of [delta][[rho].sub.s]/[delta]t of material per unit time.
Equation (2)
describes the pyrolysis process itself in terms of a single
first order,
Arrhenius type (13-16) rate law. The
factor A is the
frequency, or
pre-exponential, factor, E is the activation energy for the
pyrolysis
reaction, and R is the universal gas constant; R=1.987 cal/mole[degree]C-8.314
J/mole[degree]C.
Again, [[rho].sub.s], is the density of the
pyrolyzing solid while
[[rho].sub.a]
is the density of the portion of the solid which gasifies.
Equation (3)
is the continuity equation expressing the change in density
with time,
[delta][[rho].sub.s]/[delta]t, in terms of the flow of mass, [[rho].sub.g][V.sub.g],
out of the pyrolyzing
solid.
In all these
equations, the pyrolyzing solid is assumed to consist of a
char matrix,
density [[rho].sub.c], and an active or gasifiable portion of density
[[rho].sub.a].
The thermophysical properties of the pyrolyzing
solid are assumed to
be given by
linear interpolation between those of the virgin wood and
those of the
char as a function of density. For
example, the thermal
conductivity
of the pyrolyzing solid is given by <see equation below>
bsex180a.gif (204x594)

where the
subscripts, c, s, and w, are char, pyrolysing solid, and virgin
wood.
Typical
boundary conditions for this set of equations are to set all the
temperatures
to ambient and all the properties to that of virgin wood at
time t=0. At
t=0 a heat flux Q(t) is then applied to the exposed surface <see equation
4>
bsex181.gif (75x726)

which raises
the temperature of the system and begins the decomposition
process.
Additionally, at some point, x=s, into the
wood it is assumed to
be perfectly
insulated, [delta]T/[delta]x=0, and that there is no further flow of
volatiles,
[[rho].sub.g][V.sub.g]=0
Equations
(1-3) and boundary conditions (equation 4 plus the above
discussion)
can be formulated into a set of finite difference equations
and solved as
done in (22) and others. Typical values
used are listed in
Tables (1,9,
10) but vary dramatically between studies (1,8,9,17-33).
Numerous
additional considerations can be taken into account in modeling
pyrolysis.
Among these are adapting to different
geometries (23,25);
accounting
for radiant and convective heat losses from the surface (26);
and
accounting for the volatiles that escape into the virgin wood as well
as through
the char (26). Other factors that
should be considered include
TABLE 10
Constants for the Pyrolysis of
Wood, Equation (2)
A
E
Ref
5x[10.sup.9] g/[cm.sup.3] s
35 kcal/mole
33 path 1
3x[10.sup.17]
55
33 path 2
5x[10.sup.7](*)
30
22
2.5X[10.sup.4]
18
20, 26
5x[10.sup.8]
33
17
(*) In this
case A is expressed in terms of 1/sec rather than gm/[cm.sup.3]s
so that other
factors must be adjusted accordingly.
TABLE 11
Pyrolysis Yield For Different
Contaminants
Charcoal
Tar
[H.sub.2]O [CO.sub.2]
CO
No
additive
30%(*) 46%
19%
4% 1%
.14% Wt/Wt
[Na.sub.2][CO.sub.3] 85
3
8 2
2
8% Wt/Wt
NaCl 51
6
29 7
7
(*) By weight
percent
Reference (3)
the effects
of char cracking, multiple chemical decomposition (or pyrolysis)
pathways and
energetics, shrinkage of the char matrix, simultaneous
char
combustion, and simultaneous char-volatile reactions.
In
particular, it is important to note that there are at least two
chemical decomposition
paths (9,28,33) for cellulose alone.
The first
predominates
at low temperatures, 200-280[degrees]C, and consists of "dehydration"
or the
removal of water from the cellulose leaving considerable char and
producing
little combustible gas. The second
predominates at higher
temperatures
(280-340[degrees]C) and is a depolymerization process producing
mostly
combustible gases with little or no char left behind (28,33).
Because of
the presence of alternative pyrolysis paths, relatively low
concentrations
of contaminants can shift the relative yield of char
considerably
depending on which path is emphasized.
This is illustrated
dramatically
in Table 11 and examined in greater detail in reference (18).
In the
absence of contaminants, however, the yield of char from the
pyrolysis of
wood is relatively insensitive to its temperature history (3)
with only its
volatile content varying with temperature as already
discussed.
For further information on the chemistry of
pyrolysis the
interested
reader is referred to reference (33); on the thermodynamics of
pyrolysis,
(30), and on the kinetics of pyrolysis, (31).
Charcoal
Combustion
Following
(and during) loss of the volatiles by pyrolysis, the remaining
char burns by
oxidation at its surface. Basic reviews of this process are
given in
references (13,14) and are summarized below.
The most
simple model of carbon combustion considers only the two following
reactions(1):
2CO + [O.sub.2] [right arrow]
2[CO.sub.2]
(5a)
C + [CO.sub.2]
[right arrow] 2CO
(5b)
Experimentally,
it has been found that carbon leaves the surface of the
charcoal
primarily in the form of CO. Diffusing
away from the surface,
the CO
encounters and burns with [O.sub.2] through a variety of intermediate
reactions(1)
in the gas phase to form [CO.sub.2] (reaction 5a).
This reaction can
sometimes be
seen as a faint bluish flame just above the surface of the
charcoal.
Part of this [CO.sub.2] diffuses back to the
surface where it is
reduced to CO
by the solid carbon (reaction 5b) thus closing the cycle.
The mass
fractions for these various reactants are shown schematically in
Figure 2.
bse2x184.gif (600x600)
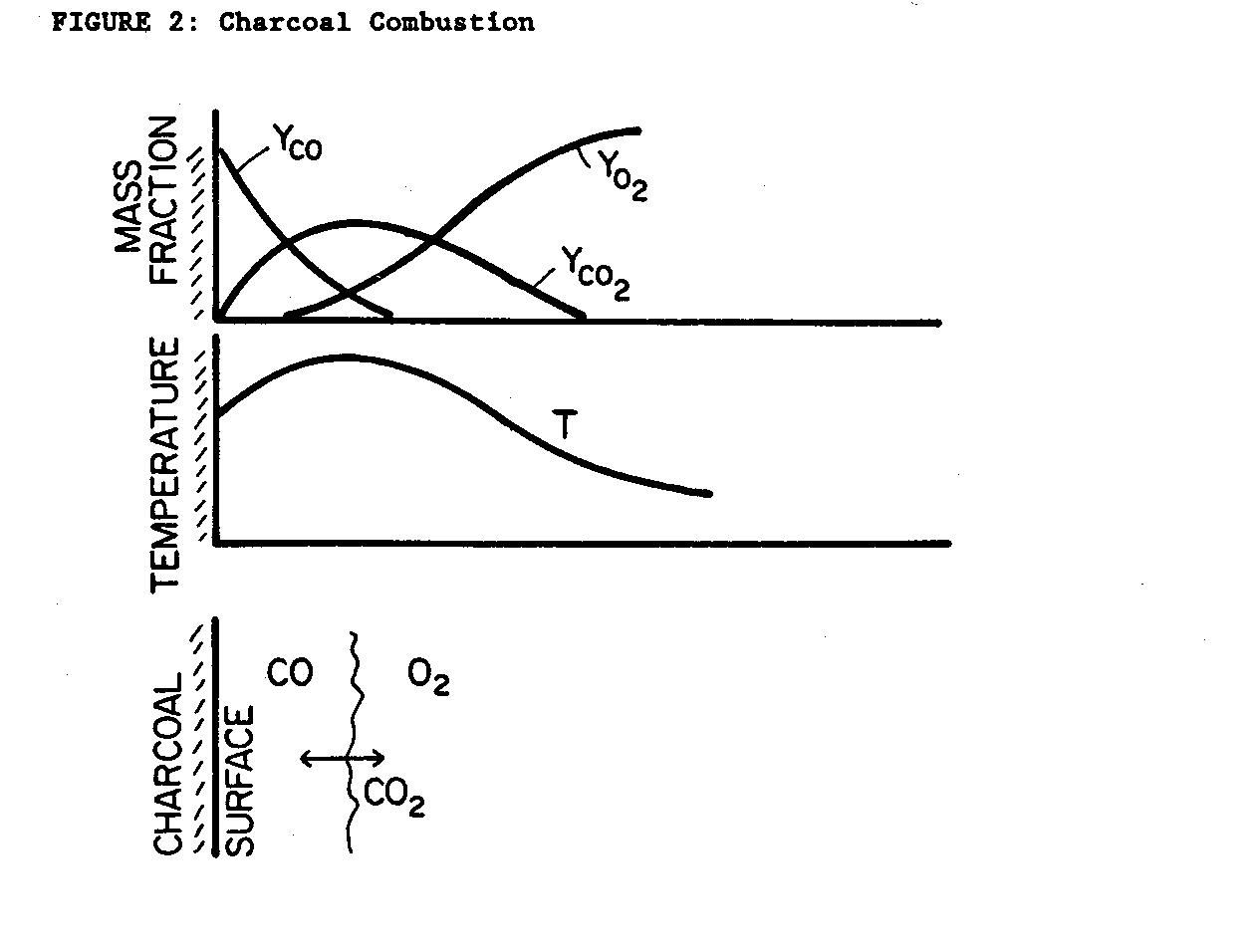
________________________
(1) A variety
of reactions with OH, [HO.sub.2], [H.sub.2][O.sub.2], and other intermediate
hydrogen-oxygen
radicals are necessary to fully explain the observed
behavior of
carbon and carbon monoxide combustion (47). Modeling of this
system is
also discussed in (47).
The law of
conservation of species in spherical coordinates for this
highly
simplified system is then <see equation 6a>
bsex6a.gif (95x660)

for oxygen,
subscript o, and <see equation 6b>
bsex6b.gif (95x660)

for carbon
dioxide, subscript d. The variable
[[rho].sub.g]. is the density of the
gas;
[R.sub.c] is the radius of the carbon sphere; [Y.sub.o] or [Y.sub.d] is the
mass fraction
of that
chemical species, [Y.sub.o]=[P.sub.o][M.sub.o]/PM, where P is the pressure and
M is the
molecular
weight; [W.sub.o] or [W.sub.d] is the rate of reaction (moles/volume-sec) of
that species;
[M.sub.c] is the mass flux (mass/area-sec) of carbon from the
surface of
the charcoal sphere; and [D.sub.o] or [D.sub.d] is the species diffusivity.
If [f.sub.c]
grams of carbon react with 1 gram of [CO.sub.2] at the surface of the
charcoal to
form (1+[f.sub.c] grams of CO, if [f.sub.m] grams of CO react with 1 gram
of [O.sub.2]
to form 1+[f.sub.m]) grams of
[CO.sub.2], and if the species diffusivities are
equal,
[D.sub.o]=[D.sub.d]=D, then the burning rate of the charcoal can be calculated
(13) and is
given by <see equation 7a>
bsex7a.gif (104x726)

and the
particle lifetime (characteristic time until it burns
up) is
<see equation 7b>
bsex7b.gif (204x660)

where
[[rho].sub.c] is the density of the carbon sphere.
In reality,
there are numerous complications to this simple theory
(34-42).
Among these are: the presence of volatiles
and char-gas reactions
(30,31); the
presence of water vapor speeding the conversion of CO
to [CO.sub.2]
(35,47); radiant heat loss which in some cases leads to spontaneous
extinction of
combustion for small particle sizes (36); the effect of
pores and
cracking on diffusion rates (37,38); the effect of varying
reaction
rates, and of heat and mass transport (38,40); the effect of
thermal
inertia (39); the effect of the outer ash layer slowing diffusion
of gases to
the burning surface (10,11); and the departure from equilibrium
(41,42).
In
particular, the ash layer of non-combustible salts remaining on the
surface of
burning charcoal is an important factor controlling its rate of
combustion
(10,11). In turn, this regulates the
power level of charcoal
stoves and
does so in a useful manner: providing high power levels at the
early part of
cooking and then lower power levels as the ash forms (43).
Raising the
power level again is done simply by moving the pot and
knocking off
the ash layer.
A variety of
things can be done to improve the combustion quality of a
stove.
Among these are insulating to raise
combustion chamber temperatures;
increasing
the volume (and particularly the height of the combustion
chamber) so
that there is more complete burn-up before the hot gases
come into
contact with the pot and combustion is quenched (this does,
however,
reduce radiant heat transfer to the pot); provide swirl to the
incoming
gases to improve mixing; provide baffling in the combustion zone
to create
recirculation zones to better burn the gases; and to use a grate
to provide
the charcoal firebed oxygen with which to burn (this improves
the overall
combustion, reduces the wasted charcoal, and can raise fire
powers
(44,45)). A number of these were
discussed in Chapter III.
Diffusion
Flames, Soot, and Air Quality
When
pyrolysis gases, or volatiles, leave the wood they either escape as
smoke or they
burn in the yellow flame above the wood.
Such flames are
known as
diffusion flames because their overall speed of combustion is
controlled by
the rate at which oxygen can diffuse to the burning volatiles
rather than
being controlled by the rate of the oxygen-hydrocarbon
kinetics
themselves. Diffusion flames are
discussed in detail in basic
combustion
texts (13-16). Due to the complexity of
flaming combustion of
wood, the
topic will only be briefly surveyed here.
The pyrolysis
gases consist of over 200 different compounds (46).
In the
lower part of
the flame, these gases react to produce free carbon in the
form of soot
and carbon monoxide which then burn in the upper part of the
flame. The
combustion of carbon monoxide generally occurs through carbon-hydrogen-oxygen
reactions
including primarily CO+OH-[CO.sub.2] + H which is much
slower than
the rate of reaction between OH radicals and typical hydrocarbon
species
(47). Thus, although much CO is
produced in the lower part
of the flame
its subsequent combustion to [CO.sub.2] is retarded until most of
the
hydrocarbons have been consumed (47).
Although, as already discussed,
wood with a
moisture content of 20 to 30 percent has better overall
combustion
efficiency than oven dry wood, this may not be due to catalysis
by OH
radicals or other mechanisms (48) but perhaps simply to limiting the
migration of
volatiles out of the combustion zone.
In fact, measurements
have shown
that higher wood moisture contents can lead to greater CO
production
(49).
Because CO is
preferentially burned in the upper part of the flame,
bringing the
pot too close to the flames may then quench the combustion of
carbon
monoxide and cause larger amounts to be emitted, increasing the
health
hazard. What very little data there is
on this factor suggests
that for some
stoves, CO production does increase when the pot is brought
very close to
the fire (49). This is an important
factor that needs to be
examined much
more carefully.
The carbon
that agglomerates into soot burns in the manner already
discussed above
under Charcoal Combustion and gives off the characteristic
yellow flame
of a wood fire (Appendix C). The
estimated time to burn up a
carbon
particle, equation (7b), can be balanced against the average time
that that
particle is in the combustion zone (height of combustion zone
divided by
average velocity) to determine, simplistically, whether or not
it burns up
completely or escapes as soot. Moving
the pot closer to the
fire then
reduces the time for combustion and can quench soot combustion
before it is
complete. This will increase the amount
of soot/smoke that
escapes the
fire. A particularly simple example of
this can be observed
by placing an
object in the flame of a candle to produce candle black.
The
mechanisms leading to soot production are not yet well understood (50-52).
For
thoroughly premixed fuel-air flames, the production of soot is
determined by
the rate at which the volatile gases pyrolyze leaving carbon
behind which
then subsequently agglomerate and grow into large soot particles
and the rate
at which these soot particles burn up by oxidation.
In general,
as the temperature is raised the particles burn (oxidize)
faster than
they pyrolyze and agglomerate (51).
Thus, in this case,
higher
temperatures reduce soot.
In contrast,
under some diffusion controlled conditions, raising the
temperature
increases the rate of pyrolysis and increases the tendency to
soot
(51). In general, the tendency to soot
will depend on the fuel flow
rate, flame
temperature, oxygen diffusion and the particular molecule
involved
(51).
In
woodstoves, as the flame height (and contact with the pot) increases
with the
firepower, the amount of soot produced can be expected to
increase with
firepower as well. Under typical
operating conditions for
small stoves,
as much as 40 grams and more of particulates can be released
per kilogram
of wood burned with values of 5 g/kg more typical (53) (see
Table II-16).
In terms of
overall stove efficiency, incomplete combustion, as evidenced
by carbon
monoxide, soot, and smoke production, has little effect.
However,
these are very important in terms of user health (53).
A number
of compounds
emitted by wood fires have been identified as carcinogenic
and the total
exposure to particulates, carbon monoxide, and carcinogens
such as
Benzo-a-pyrene suffered by users are often considerably above
recognized
health standard recommendations (53).
Raising the average
combustion
zone temperature can reduce these emissions - - with the
greatest
reduction occuring for temperatures in excess of 600[degrees]C (44).
For the
interested reader, information on modeling diffusion flames is
given in
references (13-16,54) and the case of the open wood fire is
specifically
treated in reference (45).
APPENDIX
E: HEAT EXCHANGERS
Detailed information
on heat exchanger design is given in (1-6) and the
interested
reader is urged to consult these sourcebooks.
Although the
following
calculation is for the case of forced convection, the concept of
counterflow
heat exchange can be similarly applied to flows driven by
natural
convection. As the example below
clearly indicates, the potential
of heat
exchangers to improve the performance of traditional energy
technologies
is enormous.
The
air-to-air heat exchanger discussed in Chapter VI for the high
temperature
foundry is an especially simple form to analyze.
Effectively,
it consists
of two parallel streams of gas moving in opposite directions,
bounded and
separated by thin sheets of steel.
Because it is a closed
system, the
air flow in this heat exchanger is constant and the same going
in and
out. The situation is illustrated in
Figure 1.
bse1x188.gif (540x540)

In this
figure, T is the temperature, the subscripts h and c refer to the
hot and cold
gas streams, and i and o refer to the streams incoming to and
outgoing from
the heat exchanger. The heat exchanger
itself is L long, W
wide, and
formed of two adjacent ducts each with a gap G.
The ducts are
bounded by
steel of thickness [s.sub.m] and conductivity [k.sub.m].
Then, the
following equation is used for the change in air temperature: <see equation
1>
bsex187a.gif (129x726)

where dE is
the change in heat energy of an object of mass m and specific
heat
[c.sub.p] due to a temperature change within that object of dT.
Applying
this equation
to a volume element WGdL with a constant mass flow through
it of m[.],
where the dot indicates a time derivative, (dm/dt)=m[.], the heat
exchange per
unit time is Q=(dE/dt), or <see equation below>
bsex187b.gif (199x798)

where
with [bar] V
and [bar] [rho] being the average gas velocity and density within that volume
element.
Since this is
a closed system and ignoring the roughly five to ten percent
increase in
the mass of the gas when the combustion products are added,
m[.]h=m[.]c.
Further, the external walls of the heat
exchanger are assumed to
be perfectly
insulated and the gas properties, such as [c.
sup.p],
constant. In
this case,
the cold and hot gas streams have equal and opposite temperature
changes and
([T.sub.h]-[T.sub.c]) is constant and the same for all dL.
Next, the
convective heat transfer can be written
Q = d (hAT) = hAdT
(5)
This equation
gives the heat transfer per unit time from one object to
another when
they have a common surface area of A, a heat transfer
coefficient
of h and a temperature difference dT.
In this
system, typical gas velocities are low resulting in laminar flow.
As the
temperature difference between the hot and cold streams is everywhere
constant,
there is a constant heat flux. The
Nusselt number then
used is
(Appendix B): <see equation 6>
bsex188a.gif (95x660)

where G is
the characteristic dimension of the duct, k is the thermal
conductivity
of air, and h is the convective heat transfer coefficient
between the
gas and the wall.
For an area
element dA, the heat transfer from one gas stream to the other
can now be
written as: <see equation 7>
bsex188b.gif (106x660)

where the
Fourier conduction law has been used.
As the thermal conductivity
of air is
typically [10.sup.-3] that of steel, this reduces to: <see equation
below>
bsex189a.gif (181x726)

where
[bar] k [approximate] 1/1/[k.sub.h] +
1/[k.sub.c] [equivalent] k t
Now using
equations (2,3,8) the following can be written for the entire
heat
exchanger: <see equation below>
bsex189b.gif (224x726)

The inlet
temperatures [T.sub.ci] and [T.sub.h1] can be assumed to be known.
Then, [T.sub.co]
and
[T.sub.ho] can be solved for to find: <see equation 10>
bsex189c.gif (278x726)

and the
efficiency of the heat exchanger is given by: <see equation 11>
bsex189d.gif (181x726)

A kilogram of
charcoal requires roughly 9 [m.sup.3] of air at standard temperature
and pressure
(STP) for stoichiometric combustion. A
one kW fire
then burns
3.45x[10.sup.-5] kg/s of charcoal and 3.1x[10.sup.-4] [m.sup.3]/s of STP
air. With
an excess air
factor of 2, 7.3x[10.sup.-4] kg/s of air flow into the heat
exchanger and
7.65x[10.sup.-4] kg/s of combustion products flow out.
Averaging,
roughly
7.5x[10.sup.-4] kg/s of mass flow through the heat exchanger for a 1 kW
fire.
For the effective specific heat, an average
value of 1.1x[10.sup.3] J/kgK
is used and
for the effective thermal conductivity [bar] k an average value of
0.027 W/mK is
used (Table A-4) which is relatively constant independent of
the
temperature difference between the gas streams.
From equation
(11) it can be seen that the efficiency of heat recuperation
is improved
by making the duct gap G thinner and the duct area LW larger.
However, the
thinner and longer the duct, the greater the pressure drop
and the more
work that is needed to force the gas through the system.
Additionally,
as the pressures increase, the more air that will leak
directly out
of the furnace and completely bypass the heat exchanger.
The pressure
drop in laminar forced convection is (Table B-2, page 159,
and equation
(4) above): <see equation 12>
bsex190a.gif (116x726)

where (2L) is
the total duct length and [bar][nu] is the kinematic viscosity of
the gas and
for convenience here is averaged over the entire length of the
hot and cold
streams. For assumed inlet temperatures
of 300 and 1,300 K,
[bar][nu]=89x[10.sup.-6]
[m.sup.2]/s and [bar][rho]=0.724 kg/[m.sup.3].
Using the relation Power-forcexvelocity
we then find:
<see equation 13>
bsex190b.gif (93x726)

Graphs based
on equations (11) and (13) are presented in Chapter VI.
As can be
seen from Figure VI-4 and from equations (11) and (13), the
pressure drop
increases very rapidly with the duct gap, the efficiency
only
moderately so. As the gap is reduced,
the point where large amounts
of fan power
are needed is quickly reached. As the
available fan technology
in most
developing countries is limited and the motive power is
usually
human, it is important to minimize the pressure drop that must be
overcome
within the heat exchanger. An improved
fan technology may be
needed
regardless. A typical starting point
might be a heat exchanger 2 m
long, 0.5 m
wide and with a duct gap of 6 mm. This
would provide, in
principle, a
70 percent heat recovery at a cost of 12 watts in blower
power.
A much wider duct, W, could be used but
ensuring that the gas
flows
uniformly across the entire area is difficult.
It should
also be noted here that with heat recuperation, the necessary
mass flow in
through the system is reduced roughly proportionally, which
further
improves the efficiency of heat recuperation and reduces the power
needed for
the fan.
With the
above parameters the Reynold's number is: <see equation 14>
bsex190c.gif (114x798)

which gives
laminar flow.
The steady
state gas temperature can also be estimated.
With an excess
air factor of
2, 1 kg of charcoal requires 21 kg of air for combustion and
provides
29,000 to 34,000 kJ of energy.
Assuming an
average specific heat of 1.2x[10.sup.3] J/kgK, there will be a
temperature
rise of: <see equation below>
bsex190d.gif (135x600)

This,
however, ignores a number of large losses including the dissociation
of the
combustion products which will be significant at these temperatures.
For a more
precise calculation, the reader should consult a text
on
combustion.
Finally,
because of the high temperatures within the system, there can be
significant
thermal expansion of the metal and possibly warping and
buckling.
As the thickness of the ducts is important,
the effect of this
thermal
expansion should be taken into consideration.
The
coefficient of thermal expansion, [alpha],ranges from about
11x[10.sup.-6]/[degrees]C at
room
temperature to about 15X[10.sup.-6]/[degrees]C at 750[degrees]C for steel
(7). Consider,
for example,
an air to air heat exchanger formed from three concentric
cylinders for
which at room temperature the inner wall has an outer
diameter of 1
meter and the outer wall is of 2 mm thick metal with an
outer
diameter of 1.016 meters (or a duct gap of 6 mm).
If when in
operation, the inner wall has a temperature of 530 [degrees]C, its
diameter will
be 1.0063 meters ([alpha]=12.5x[10.sup.-6]).
If the middle wall is
instead at
330 C, its outer diameter will be 1.0197 meters.
Thus, instead
of a 6 mm gap
there is a 4.7 mm gap. This could make
an important difference
in the
performance of the furnace.
To avoid this
problem it is then preferred to make the heat exchanger out
of parallel
sheets of metal as described in the text, with spacers between
the shells to
maintain the desired duct gap. To
prevent the assembly from
warping due
to differential expansion during operation, the individual
sheets can be
left free to slide back and forth past each other with a
rigid
external frame holding the entire assembly in place.
This will also
allow easy
disassembly and cleaning.
TABLE 1
Linear Thermal Expansion
Coefficients
[degrees]C
Aluminum
Steel
Steel Steel
Steel
(.1%
C) (hard)
(Ni)
(soft)
50
.0234x[10.sup.-3] --
--
--
--
100
.0238
.012x[10.sup.-3] .01170x[10.sup.-3]
--
--
200
.0245
-- .01225
--
.01255x[10.sup.-3]
300
.0255
-- .01277
.00933x[10.sup.-3]
.01307
400
.0265
-- .01328
.01000
.01360
500
.0274
-- .01382
.01050
.01412
600
.0283
-- .01433
.01042
.01465
700
-- --
.01486
.01114
.01519
800
-- --
--
.01156
--
900
--
--
--
.01167 --
1000
--
--
--
.01185 --
Reference
(7)
APPENDIX
F: FINANCIAL ANALYSIS
Simple
financial analyses of improved stoves can only provide a general
indication of
potential benefits. Numerous factors
such as reduced smoke
inhalation,
greater convenience in cooking, and a modern image may well
prove to be
more important in the decision to purchase an improved stove
than the
potential financial savings for those who purchase fuel.
And even
for those who
purchase fuel, it is difficult to realistically estimate the
barrier posed
by the first cost of the stove. Among
the factors that tend
to raise this
barrier are a short-term view -- no longer than through the
next harvest
and often considerably shorter; a narrow margin of survival
-- so that
risks must be very carefully weighed; and a simple lack of cash
to
invest. World Bank data for commercial
interest rates for agricultural
credit show
rates as high as 192 percent, with most countries falling in
the 20 to 66
percent range (cited in 1). Thus, the
first cost of an
improved
stove can be a truly formidable barrier and must be taken into
account.
The first
cost of a stove can be an even greater barrier to those who
forage for
fuelwood or other fuel rather than purchasing it, In this
case, the
monetary cost of a stove is balanced against the labor of the
forager -- in
many cases a child who may not have any other immediately
useful task
to perform in place of foraging.
Obviously, the head of the
household
will often choose against such a purchase when there are ready
hands
available.
Financial
analyses of projects which receive government or international
donor support
and which do not themselves earn revenue must also take into
account that
it is often easier to get one-time funds to install project
equipment
than it is to get recurrent funds for operation and maintenance
(2).
Initial capital investment can often be
obtained through aid programs,
liberal
financing, or one-time budgeting, while recurrent costs
must come out
of the regular budget and must compete against all the other
needs of
education, rural assistance, and infrastructure development.
The
ability to
meet recurrent costs is often far more important than minimizing
life cycle
costs as measured in a single present value (2).
Combining
initial
capital and recurrent costs into a single present value
ignores the
crucial differences between their funding sources and restrictions.
In many cases
it may be better to perform undiscounted comparisons
of capital
and recurrent costs separately (2).
Developing countries are
littered with
projects and equipment in which recurrent costs could not be
met.
In stove projects, an extra effort must be
made to ensure that sales
can meet
recurrent costs.
With these
caveats, simple financial analysis techniques will now be
considered.
As a simple first example, consider the case
of a traditional
stove and two
improved models (ignoring effective interest rates) as
listed in
Table 1. As seen there, at the end of
the first year both
improved
models have nearly identical financial savings relative to the
traditional
stove despite widely differing first costs and efficiencies.
Because the
lifetimes and other characteristics of stoves can vary so
dramatically,
it is often convenient to spread their cost over their
entire
lifetime. The results in this same case
with no interest rate, are
presented in
Table 2. Additional costs to be spread
over the lifetime of
the stove
include maintenance.
Calculations
such as these with no interest factors are extremely simple
and numerous
variations can be tried to observe the relative importance of
different
parameters such as the cost of fuel, the cost of the stove, the
energy
savings of the stove, and so on. As the
interest rate is assumed
zero, each of
these factors will have a linear interdependence.
TABLE 1
Financial Analysis of Three
Hypothetical Stoves
Daily
Accounting
EXPENDITURES, US$
Traditional
Improved
Improved
Metal Stove
Stove A
Stove B
(30%
Savings) (40% Savings)
Day
Daily Total
Daily
Total Daily
Total
Installation
0
-$0.50 -$0.50
-$6.50
-$6.50 -$15.5
-$15.5
Fuel
1
- 0.25 - 0.75
-
.175 - 6.675
-
.15 - 15.65
Fuel
2
- 0.25 1.00
-
.175 - 6.85
-
.15 - 15.80
Fuel
3
- 0.25 - 1.25
-
.175 - 7.025
-
.15 - 15.95
Fuel
4
- 0.25 - 1.50
-
.175 - 7.20
-
.15 - 16.10
....
...
... ...
...
... ...
...
365
- 0.25 -91.75
-
.175 -70.375
-
.15 - 70.25
Simple
payback time (days)
80 150
Savings over
one year
21.38 21.50
TABLE 2
Financial Analysis of Three
Hypothetical Stoves:
Daily
Totals
Traditional
Improved Improved
Metal
Stove Stove A
Stove B
Installation
US$)
0.50
6.50 15.50
Lifetime
(years) 1
2
4
Installed
cost/day(*) (US$) 0.00137
0.008904
0.0106
Energy
savings relative to
traditional
stove (percent) --
30
40
Fuel
cost/family-day (US$) 0.25
0.175
0.15
Total operating
cost/day (US$) 0.25137
0.1839
0.1606
(*) Interest
rate is assumed zero.
In the more
general case, the effective interest rate must be taken into
account.
The effective interest rate can be thought
of as a quantitative
representation
of the barrier opposing the purchase of a stove by a poor
person.
The higher the interest rate the greater the
value placed on
having the
money in hand at the moment rather than investing it in something
that will
only provide a financial return in the future.
To calculate
simple interest, the formula
F = P(1+ni)
(1)
is used,
where P is the present value of the investment, i is the interest
rate per time
period, and n is the number of time periods.
The factor F
is the value
of the investment n time periods into the future.
Thus, if
$10 are put
into the bank at a simple annual interest rate of 20 percent,
then the
future worth, F, of that investment one year in the future is
F=$10(1+0.2)=$12;
two years in the future F=$14, and so on.
To calculate
compound interest (the more general case), the formula
F = P[(1+i).sup.n]
(2)
is used.
Thus, at the end of each time period, the
entire investment P
plus interest
i gained during that time period is reinvested at that
interest rate
i. For the above example, the future
worth F of the $10
investment at
the end of each year is given in Table 3.
Alternatively,
the present value P of some worth is given by P=F/[(1+i).sup.n].
Thus, at an
interest rate of 20 percent, being promised $24.88 in five
years is the
same as being given $10 immediately.
If n equal
payments, E, are regularly made over a period of time, then the
future worth F
of these payments is simply the sum <see equation 3>
bsex195a.gif (165x660)

The
corresponding present worth P is <see equation 4>
bsex195b.gif (93x726)

where n is
the number of periods over which the payments E are made and i
is the
interest rate over each period. This
can also be expressed as
spreading a
single down payment P over a number of smaller payments E out
into the
future.
As an
example, the above case can be considered with a nominal annual
interest rate
of 40 percent or a nominal daily rate (40/365) of 0.11
percent.
Spreading the cost P of the traditional
stove A and stove B into
n equal daily
payments E over the lifetime of the stove, the daily cost of
operating the
stove can be calculated as shown in Table 4.
bsex196.gif (600x600)

It should be
noted that the effective annual interest rate, when compounded
over a period
of less than a year, is <see equation 5>
bsex196a.gif (75x726)

for
compounding the nominal interest rate, r, (c) times during the year.
As
c becomes
very large, compounding every week or less, this can be written <see
equation 6>
bsex196b.gif (85x660)

where e is
the base for natural logarithms, e=2.71828.
In the above case,
the nominal
annual interest rate of 40% becomes, with daily compounding,
an effective
annual rate of approximately
[e.sup.0.40] -1 = 0.4918 or 49%
TABLE 3
Compound Interest
Year
[(1+i).sup.n]
F
0
1 $10.00
1
[1.2.sup.1] 12.00
2
[1.2.sup.2] 14.40
3
[1.2.sup.3]
17.28
4
[1.2.sup.4] 20.74
5
[1.2.sup.5] 24.88
With these
formulas, a wide variety of situations can be analyzed.
More
complicated
situations, such as with inflation, can similarly be analyzed
using
standard interest rate formulas presented elsewhere (3).
For the
calculations above, an effective interest rate must be assumed and
is often
based on very dubious assumptions. To
avoid this, a factor termed
the internal
rate of return is calculated which does not depend on any
particular
assumed interest rate. Its disadvantage
is that it is usually
more
difficult to calculate.
The internal
rate of return is the interest rate that sets the total
present
worth, receipts plus disbursements, to zero.
As an example, for
stove model A
listed in Tables 1, 2, and 4, there is a disbursement of
$6.50 on day
zero and receipts of $.075 each day in fuel savings over a
two year
period. The internal rate of return is
that interest rate which
gives a
present value of $0.00 for all these costs. <see equation 7>
bsex197a.gif (116x726)
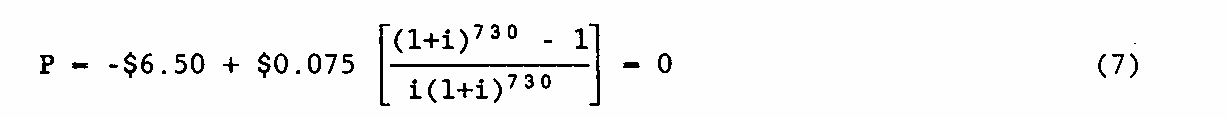
Because the
interest rate is so high, this can be solved directly.
Thus, <see equation 8>
bsex197b.gif (118x660)

This is a
nominal annual rate of 365(0.0115)=420 percent.
In this particular
case, the
internal rate of return decreases almost linearly with the
decreasing
price of fuelwood, the decreasing fuel efficiency of the stove,
or the
increasing initial cost of the stove.
As a second
example, more typical of rate of return calculations, consider
a stove which
costs $20.00 and saves $0.20 worth of fuel per week the
first
year. Due to losses in performance, the
stove saves $0.16 per week
the second
year, $0.12 per week the third year, $0.08 the fourth year, and
$0.04 the
fifth year. When the stove is
purchased, its present value is
then <see
equation 9>
bsex197c.gif (106x660)

where (Fuel
X) is the present value of the fuel used during the year X at
the beginning
of that year, the factor N is given by N=[(1+i).sup.52], and i is
the weekly
interest rate. The factor N discounts
the value of the fuel
during any
particular year to its present value at the time the stove is
purchased.
The present value of the fuel during any
particular year X is
given by
equation (4); <see equation below>
bsex198a.gif (204x660)

and so on
.....
For each
weekly interest rate the present value is then calculated from
equations (9)
and (10). Results are shown in Table
5. As can be seen, the
internal rate
of return is between 25 and 30% and can be roughly estimated
to be 27%.
In closing
this section it is important to note that it has dealt with
financial
analysis for the individual stove user only.
In determining the
value of a
stove program it is also important to consider the economics,
that is, the
national environmental costs of doing nothing; the impacts of
stove
programs on rural and urban employment; the national costs of
importing
substitute fuels or subsidizing stove dissemination; the cost of
infrastructure
development; and many others. Some of
these were briefly
discussed in
Chapter II.
TABLE 5
Internal Rate of
Return
Interest
Capital
Savings(**) (by year)
Rate(*)
% Investment
1
2 3
4
5 Total
0.002
-$20.00
$9.87 $7.12
$4.81
$3.01 $1.30
+$6.10
0.003
-20.00
9.62 6.58
4.23
2.41 1.03
+3.87
0.004
-20.00
9.37 6.09
3.71
2.01 0.82
+2.01
0.005
-20.00
9.14
5.64
3.26 1.68
0.65
+0.36
0.006
-20.00
8.91 5.22
2.87
1.40 0.51
-1.08
0.007
-20.00
8.69 4.84
2.53
1.17 0.41
-2.36
(*)These are
weekly interest rates and correspond to nominal annual
interest rates of approximately 10, 15,
20, 25, 30, and 35%.
(**)Savings
are due to reduced fuel costs. Column 1
is given by
(Fuel 1) above; column 2 is given by
(Fuel 2)/N; column 3 by (Fuel
3)/[N.sup.2]; etc. corresponding to the
terms in equation (9).
APPENDIX G:
STATISTICAL METHODS
This appendix
is a brief "how to" review of a number of basic statistical
techniques
including the average, standard deviation, coefficient of
variation,
confidence limits, t-test, and linear regression.
Those
interested in
more detailed information or more advanced techniques should
consult a
basic text on statistics such as reference (1).
Statistical
techniques are very useful in quantifying data and can
sometimes
assist one's understanding of the physical or social processes
that are
occurring. However, these techniques
are not a substitute for
understanding
these processes. Such understanding is
developed instead,
for example,
by analyzing the combustion and heat transfer processes in a
stove or the
cultural and social response in adapting to a new stove.
When
statistical analysis of the data is done mechanically, without an
understanding
of these underlying physical or social processes, important
factors may
be obscured that might otherwise be seen by carefully reviewing
the raw
data. Thus, statistical techniques are
a tool to be used with
care.
Finally, it
is important to note that most of the following statistical
techniques
are based on certain simplifying assumptions about the nature
of the test
data being analyzed. In particular, it
is assumed that the
test data are
always a random sample of an underlying "normal" or gaussion
distribution.
Although this is usually a reasonable
approximation, it is
not
guaranteed, and applying the following statistical techniques to data
that are not
"normal" can sometimes lead to significant errors.
These
techniques
should therefore be used with caution.
For the interested
reader,
reference (1) discusses various tests to determine whether or not
a sample can
be treated as "normal" and, if not, alternative statistical
techniques
that can be used.
Average
The average
of a set of data [x.sub.i] is defined as <see equation 1>
bsex199a.gif (146x726)

where[sigma]
is the sum of all the n individual test values [x.sub.i].
More precisely,
X[bar] is an
estimator of the true average value of the underlying
"normal"
distribution of which the test data are a random sample.
As the
number of
tests, n, increases to infinity, X[bar] converges to the true average
value of the
distribution.
As an
example, assume that three different stoves, A, B, and C, are tested
in the
laboratory with the results shown in Table 1.
The average for
stove A is
<see equation below>
bsex199b.gif (165x660)

TABLE 1
Hypothetical Laboratory Test Data
Test
A (PHU)
B (PHU) C (PHU)
1
204(*)
13% 15%
2
17 16
14
3
16
17
17
4
18 18
15
5
14 14
16
6
17 16
13
7
18 17
17
8
19 18
16
9
18 17
--
10
15 16
--
(*) For ease of illustration, values
are only given to two
significant figures.
In practice, a third significant figure,
i.e. 20.3 will usually be included,
assuming that the test
procedure is sufficiently reliable to
justify that precision.
the average
for B is: <see equation below>
bsex200a.gif (87x486)

and for C is:
<see equation below>
bsex200b.gif (97x600)

Standard
Deviation
The standard
deviation, [sigma], is a measure of how much variation there is
from one test
to another within the "normal" distribution underlying the
observed test
data. The sample deviation is an
estimate of the standard
deviation
based on the observed test data. If the
tests were repeated an
infinite
number of times, the sample deviation would approach and, in the
limit, be
equal to the standard deviation (2).
The sample
deviation for a test series is defined as: <see equation below>
bsex200c.gif (186x486)

and for ease
of calculation this is written as: <see equation below>
bsex200d.gif (146x726)

For the test
series on stove A above, [S.sub.A], is then calculated as
follows:
<see equation below>
bsex201a.gif (317x600)

This
calculation can be repeated for test series B and C, giving:
[S.sub.B] = 1.6193
[S.sub.C] = 1.4079
Test results
are normally expressed an the average plus or minus the
sample
deviation: <see equation below>
bsex201b.gif (150x317)

The sample
deviation, S, can also be used to predict the approximate range
over which
the data will lie if further tests are done -- assuming the
same
conditions hold.
For a set of
n data points [x.sub.i], assuming they are a random sample of a
normal
distribution, the estimated average X[bar] and sample deviation [S.sub.x] can
be found as
discussed above. The number of degrees
of freedom of this
data set is
then given by:
f = [n.sub.x] - 1
(3)
From the
t-Table, Table 2, a t-value can be found for f degrees of freedom
and various
levels of confidence/levels of significance, 100(1-[alpha])/[alpha].
The
range <see
equation 4>
bsex201c.gif (67x726)

then holds
approximately 100(1-2[alpha])% of all the data points.
As the sample
size n becomes very large so that X[bar] converges with the true
average value
of the "normal" distribution and [S.sub.x] converges with the
standard
deviation, [sigma], of the distribution then 68.27 percent of all tests
done will
have a value lying within [- or +]1[sigma] of the average.
Similarly, 95% of
the data
points will lie within [- or +]1.96[sigma] of the average, and 99% of the data
points will
lie within [- or +]2.57[sigma] of the average.
This can be seen in Table 2
for an
infinite number of degrees of freedom.
For the more
common case of finite sample size n, as in the case of
hypothetical
stoves A, B, and C above, equation (4) must be used.
As an
example, the test data for stove A has f-10-1-9 degrees of freedom.
Thus, for f=9
and [alpha]=2.5%, the t-table indicates that the interval <see equation
below>
bsex202a.gif (78x600)
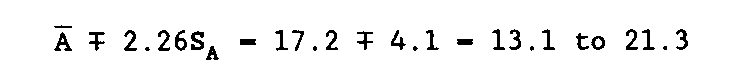
holds approximately
100(1-2[2.5])-95% of all expected data points if
testing were
to continue indefinitely (generating sample sets of 10 data
points).
Similarly,
<see equation below>
bsex202b.gif (63x486)

holds
approximately 99% of all expected data points.
For stove C
with f=8-1=7 degrees of freedom, the interval <see equation below>
bsex202c.gif (87x486)

holds
approximately 95% of all expected data points, and so on.
Coefficient
of Variation
The
coefficient of variation CV simply normalizes the sample deviation by
dividing it
by the average: <see equation 5>
bsex202d.gif (85x660)

For the test
series on stove A: <see equation below>
bsex202e.gif (108x486)

The
coefficient of variation and the sample deviation are measures of the
quality of
the data. The smaller the CV, the more
tightly grouped the
data are and
the less important the uncontrolled variables.
A very large
coefficient
of variation means that the experimental conditions are not
adequately
controlled. For example, there may be
too much wind, the
balance may
be sticking, or different testers may perform the tests in far
different
manners. Regardless, if the CV is
large, greater effort must be
made to
better control the experimental conditions and reduce the variability
of the data.
TABLE 2
t-table
Degrees
of Level of Confidence
[100(1-[alpha])]/Level of Significance
[[alpha]]
Freedom
90/10 95/5
97.5/2.5
99/1 99.5/0.5
1
3.078
6.314 12.706
31.821
63.657
2
1.886
2.920
4.303
6.965 9.925
3
1.638
2.353 3.182
4.541
5.841
4
1.533
2.132 2.776
3.747
4.604
5
1.476
2.015
2.571
3.365 4.032
6
1.440
1.943 2.447
3.143
3.707
7
1.415
1.895 2.365
2.998
3.499
8
1.397
1.860 2.306
2.896
3.355
9
1.383
1.833 2.262
2.821
3.250
10
1.372
1.812 2.228
2.764
3.169
11
1.363
1.796 2.201
2.718
3.106
12
1.356
1.782
2.179
2.681 3.055
13
1.350
1.771 2.160
2.650
3.012
14
1.345
1.761 2.145
2.624
2.977
15
1.341
1.753
2.131
2.602 2.947
16
1.337
1.746 2.120
2.583
2.921
17
1.333
1.740 2.110
2.567
2.898
18
1.330
1.734 2.101
2.552
2.878
19
1.328
1.729 2.093
2.539
2.861
20
1.325
1.725 2.086
2.528
2.845
21
1.323
1.721 2.080
2.518
2.831
22
1.321
1.717 2.074
2.508
2.819
23
1.319
1.714 2.069
2.500
2.807
24
1.318
1.711 2.064
2.492
2.797
25
1.316
1.708 2.060
2.485
2.787
26
1.315
1.706 2.056
2.479
2.779
27
1.314
1.703 2.052
2.473
2.771
28
1.313
1.701 2.048
2.467
2.763
29
1.311
1.699 2.045
2.462
2.756
30
1.310
1.697 2.042
2.457
2.750
40
1.303
1.684 2.021
2.423
2.704
60
1.296
1.671 2.000
2.390
2.660
120
1.289
1.658 1.980
2.358
2.617
[infinity]
1.282
1.645
1.960 2.326
2.576
Reference (1)
When
analyzing data, a test value quite different from all the others,
called an
"outlier", may be found, yet there may be no obvious reason to
disqualify
that particular test, e.g. no water was spilled, wood was
neither
"lost" nor misweighed, values were not misrecorded, etc.
The
presence of
such an outlier virtually guarantees that the distribution
with it
included is not "normal" and analyzing it correctly can therefore
be quite
difficult.
One way to
avoid these complications is simply to arbitrarily ignore
outliers if
they are sufficiently different from the other data.
The
consequencies
of incorrectly throwing out a "good" data point are insignificant;
the
consequences of not throwing out a "bad" data point can be
quite
adverse. One useful criterion for
deciding whether or not to
include an
outlier is to calculate how many sample deviations it lies from
the average
of the other test data. It is important
that this sample
deviation and
average not include the outlier. If it
lies more than, for
example, four
sample deviations away, the outlier should be discarded.
In
some cases it
may be desirable to use the more strict criterion of three
sample
deviations.
As an
example, consider the case where a ninth test is done on Stove C
(Table 1) and
a value of 9% is found. As already
shown, the average and
sample
deviation for the first eight tests on Stove C=15.4[- or +]1.41.
The
value 9% is
more than four sample deviations from the average, that is,
15.4-4(1.41)=9.76,
so it could be discarded.
Alternatively, consider the
case where
the ninth test gave a value of 20 percent.
A value of 20
percent is
just slightly more than [3S.sub.C] from C[bar].
Discarding this value may
be desirable
in some cases, but is not so clearly "bad" as the value 9%.
Confidence
Limits
Confidence
limits give a range of values within which the true average
value for the
data is expected to lie. As before, a
t-value is found for
the test data
with f degrees of freedom and a level of significance, [alpha].
The
confidence interval: <see equation 6>
bsex204a.gif (97x486)

is then
100(1-2[alpha])% certain (see note 3) to hold the true average value of
the
underlying normal distribution from which the test data are a random
sample.
Note the difference of 1/[radical]n compared
to equation (4). As the
number of
data points, n, gets large, the confidence interval narrows down
on the true
average value even while the scatter of data, equation (4),
remains the
same.
As an
example, for Stove A (Table 1), the range <see equation below>
bsex204b.gif (97x486)

is
100(1-2(2.5))%=95% certain to hold the true average.
Similarly, <see equation below>
bsex204c.gif (87x486)

is 99%
certain to hold the true average.
t-test
The t-test is
used to determine if two data sets differ in a statistically
significant
way.
Comparing
stoves A and B, their average and standard deviation are given
by: <see
equation below>
bsex205a.gif (97x486)

and their 95
percent confidence ranges (within which there is a 95 percent
probability
of finding their true average values -- See Note 3) are:
[A.sub.g5] = 15.9 to 18.5 and
[B.sub.g5] = 15.0 to 17.4
Thus, their
95 percent confidence limits overlap from 15.9 to 17.4.
How,
then, does
one know that stove A is actually better than stove B?
To
determine
this a t-test is used. For two data
sets x and y the t-value is
defined as
(4): <see equation 7>
bsex205b.gif (127x798)

where
[S.sub.p] is the pooled sample deviation, <see equation below>
bsex205c.gif (150x486)

[n.sub.x] and
[n.sub.y] are the number of tests used for calculating the average and
standard
deviations of data sets X and Y respectively, and the number of
degrees of
freedom is given by
f = [n.sub.x] + [n.sub.y] - 2
(8)
If the value
of t calculated by Equation (7) is larger than the value
listed in
Table 2 for that number of degreas of freedom and a certain
level of
significance, [alpha], then the data sets X and Y are said to be
different at
the 100(1-2[alpha])% level of confidence (see note 4).
It is
important to
note that the value [alpha] must be chosen from Table 2 in order to
have a
100(1-2[alpha])% confidence that the means (or averages) are different.
This is known
as a two-sided t-test of the means.
Thus,
comparing stoves A and B (Table 1) <see equation below>
bse205d0.gif (167x486)

From the
t-table, for f=18 degrees of freedom and a 100(1-2[alpha])-90 percent
level of
confidence, [alpha]=5 and t=1.734. Since
the calculated t-value above,
t=1.30, is
less than this, one says that the two stoves, A and B, do not
meet the 90
percent level of confidence requirement -- that is, there is
less than a
90 percent chance that the performance of the two stoves
differ, or
equivalently, there is more than a 10 percent chance that the
average PHU
performance of stove A is the same as that of stove B (see
note 5 for a
more detailed discussion).
Comparing
stove B to stove C (Table 1): <see equation below>
bsex206a.gif (285x486)

for
f=10+8-2=16 degrees of freedom the t-value for a 90 percent level of
confidence
([alpha]=5) is 1.746 so again [t.sub.BC]=1.10 is less than 1.746=[t.sub.90] and
there is
greater than a 10 percent chance that the true average value of
performance
for stove B will be the same as that of stove C.
Similarly,
stove C and stove A can be compared to find:
[S.sub.P] = 1.65
t = 2.30
f=16
From Table 2,
the t-value for f-16 and a 95 percent level of confidence is
([alpha]=2.5)
[t.sub.g 5]=2.12; for a 98 percent level of confidence ([alpha]-1) [t.sub.g
8]=2.583.
The t-value
for Stoves A and C is then; <see equation below>
bsex206b.gif (97x540)

Thus, there
is a 95 percent level of confidence that the performance of
Stove A is
different than that of Stove C.
Alternatively, it can be said
that there is
an approximately 2 to 5% chance that their performances are
the
same. This does not state, however,
what their relative performance
is.
Their relative performance is somewhere in
the range of values given
by their
confidence levels. For example, it is
95 percent probable that
their true
performance lies in the ranges given by: <see equation below>
bsex206c.gif (87x600)

In the case
of stoves A and B, the data was insufficient to show a
significant
performance difference between them.
Additional tests are
needed.
To determine
the number of tests n required to show a significant difference
between two
data sets each of n data points, the following formula is
used: <see
equation 9>
bsex207a.gif (121x600)

where [bar]X
and [bar]Y are the averages for the two data sets, [S.sub.P] is the pooled
sample
deviation for sets X and Y, and u is given by, for 90 percent
confidence
levels, u=1.293; for 95 percent, u=3.61, and for 99 percent,
u=4.90 (see
note 6).
For example,
to be 90 percent confident that stoves A and B had different
performances,
the number of tests needed would be approximately <see equation below>
bsex207b.gif (121x540)

or about 25
tests of each stove. The 99 percent
confidence level requires
about 71
tests of each. Clearly, if possible, it
is preferable to more
carefully
control the tests so that there is less variation between tests;
that is, to
reduce the sample standard deviation.
Thus, reliable testing
results are
more easily achieved by better controlling the variables such
as wood
moisture content, wind, etc., than by trying to overpower them by
"endlessly"
repeating tests.
Linear
Regression
Linear
regression is used to find the "best" linear relationship between
two
variables. If the relationship between
the variables is not linear,
then the
linear regression should be done with the appropriate combination
of variables
so that it is as close to a linear relationship as possible.
For example,
if y is approximately equal to [x.sup.2] then the linear regression
should be
done between the variable y and the variable [x.sup.2] rather than
between y and
x itself. The approximate form to use
can usually be
roughly
estimated by quickly graphing the data values, x, [x.sup.2], etc. versus
y and
observing which is most nearly linear.
The formulas
for doing a linear regression are the following:
Given n data
pairs (x,y), the best linear fit to these data points is
given by the
line: <see equation 10>
bsex207c.gif (70x600)

where m is
the slope and ([bar]Y-mX[bar]) is the y intercept.
The coefficient [bar]X of
this equation
is given by the average: <see equation below>
bsex208a.gif (162x726)

With the
definitions: <see equation below>
bsex208b.gif (600x600)

The
correlation coefficient is then given by <see equation 14>
bsex208c.gif (129x726)

and is a
measure of how well the line y=m(x-X[bar])+Y[bar] actually fits the data:
[- or+]1 in a
perfect fit; 0 indicates there is no correlation between the
variables x
and y in the data pairs ([x.sub.i],[y.sub.i]).
A confidence
region can also be determined for the regression line and is
similar to
the confidence limits for an average value discussed above.
The
confidence
region is given by the equation: <see equation below>
bsex208d.gif (230x600)

is the
estimated variance of residuals and F(2,n-2) is the upper (1-[alpha])
percentage
point of the F distribution for 2 and n-2 degrees of freedom at
the desired
confidence level (1-[alpha]). The F
distribution is listed in Table 5
below.
This is the
equation for an ellipse in variables (a,b).
Lines y =
a'+b'(x-X[bar])
with (a',b') within this ellipse fit the regression line with
the level of
confidence given by the choice of F.
Lines with (a',b')
outside this
ellipse do not fit the data to that level of confidence.
As an example
of the use of linear regression, suppose that a series of
tests is done
to determine the effect of the grate-to-pot height (all
other factors
remaining precisely the same) with the results for stoves D
and E as
shown in Table 3.
TABLE 3
Hypothetical Stove Data of PHU versus
Grate To Pot Height
H (height)
D (PHU)
E (PHU)
10 cm 30%
17%
11
28
14
12
27
16
13
25
17
14
24
18
15
23
16
TABLE 4
An Example Linear
Regression Worksheet
H
D E
HD
HE [H.sup.2]
[D.sup.2]
[E.sup.2]
10
30 17
300
170 100
900
289
11
28 14
308
154 121
784
196
12
27 16
324
192 144
729
256
13
25 17
325
221 169
625
289
14
24
18
336 252
196
576 324
15
23 16
345
240 225
529
256
Sum [sigma] =
75 157
98 1938
1229
955 4143
1610
Clearly, the
performance of this hypothetical stove D is very sensitive to
the
grate-to-pot height while that of stove E is not.
A linear regression
can be done
to determine what the best linear relationship is between the
stove
performance and the height in centimeters and to determine how
accurately
this linear relationship represents the data.
From the data
set above for stoves D and E the sums and sums of squares
and products
can be formed as indicated in Table 4.
Then <see
equation below>
bsex210a.gif (600x600)

Thus, the
best linear fit to the data for stove D is
[PHU.sub.D] = -1.4(H-12.5) + 26.1667
and there is
a very good correlation, |R|=0.99, between these data points
as shown in
Figure 1.
bse1x213.gif (600x600)

For stove E,
the best linear fit is given by
[PHU.sub.E] = 0.229(H-12.5) + 16.333
but the
correlation is not very good, |R|=0.313, as can also be seen in
Figure 1.
Similarly,
confidence regions can be determined for the above regression
lines.
With a desired level of confidence of 95
percent, the F value with
n=4 is
6.94. For stove D, the confidence
region is then given by: <see equation below>
bsex210b.gif (230x600)

For stove E
the confidence region in given by:
[(a-16.333).sup.2] +
2.9167[(b-0.229).sup.2] = 4.863
TABLE 5
F(2, n)
DISTRIBUTION
level of confidence/level
of significance
n
90%/10%
95%/5% 97.5%/2.5%
99%/1%
1
49.5
199.5 799.5
4999.5
2
9.00
19.00 39.00
99.00
3
5.46
9.55
16.04 30.82
4
4.32
6.94 10.65
18.00
5
3.78
5.79 8.43
13.27
6
3.46
5.14 7.26
10.92
7
3.26
4.74
6.54 9.55
8
3.11
4.46 6.06
8.65
9
3.01
4.26 5.71
8.02
10
2.92
4.10
5.46 7.56
11
2.86
3.98 5.26
7.21
12
2.81
3.89
5.10 6.93
13
2.76
3.81
4.97 6.70
14
2.73
3.74
4.86 6.51
15
2.70
3.68
4.77 6.36
16
2.67
3.63
4.69 6.23
17
2.64
3.59
4.62 6.11
18
2.62
3.55
4.56 6.01
19
2.61
3.52
4.51 5.93
20
2.59
3.49
4.46 5.85
21
2.57
3.47
4.42 5.78
22
2.56
3.44
4.38
5.72
23
2.55
3.42
4.35 5.66
24
2.54
3.40
4.32 5.61
25
2.53
3.39
4.29 5.57
26
2.52
3.37
4.27 5.53
27
2.51
3.35
4.24 5.49
28
2.50
3.34
4.22 5.45
29
2.50
3.33
4.20 5.42
30
2.49
3.32
4.18
5.39
40
2.44
3.23
4.05 5.18
60
2.39
3.15
3.93 4.98
120
2.35
3.07
3.80 4.79
[infinity]
2.30
3.00
3.69
4.61
Reference (1)
These are
graphed in Figure 2 below (7). As can
be seen, the confidence
bse2x213.gif (600x600)

region for
stove E is much larger than for stove D.
That is, there is a
considerable
latitude in possible choices for the line parameters for
stove E for a
given level of confidence. Stated
another way, there is
considerably
less certainty about what the regression line should really
be for stove
E than for stove D. This corresponds to
the much smaller
correlation
coefficient for stove E data than stove D.
Thus, the calculated
regression
line for stove E, for example, is the best fit to the
given data,
but other regression lines with parameters given within the
ellipse
provide nearly as good a fit (95 percent confidence level for the
given data)
to this data.
Comparing
Linear Regression Lines
It is
frequently necessary to compare two regression lines to determine
whether or
not they are parallel or perhaps even statistically indistinguishable.
To do this, a
technique similar to the t-test can be used.
Given two
sets of data: <see equation below>
bsex212a.gif (121x600)

were the
subscripts 1 and 2 on the brackets refer to the respective data
set.
First,
regression lines are fit through each separate data set as described
above.
<see equation 18>
bsex212b.gif (230x600)

where the
subscripts distinguish between data sets I and 2.
Second, the
estimated residual variance, [S.sup.2.sub.r], is calculated for each data
set as given
in equation (16).
Third, the
pooled estimated residual variance, [S.sup.2.sub.pr], is calculated for the
two data
sets. <see equation 19>
bsex212c.gif (150x600)

where the
subscripts again distinguish between the data sets.
Fourth, the
pooled t-value [t.sub.p] is calculated for the two regression lines <see
equation 20>
bsex214a.gif (167x600)

This can now
be compared to the t-value for ([n.sub.1]+[n.sub.2]-4) degrees of freedom
and the
desired level of significance, [alpha], from the t-table.
If [t.sub.p] is
greater than
that given for [t.sub.[alpha]] in the t-table then the lines are said to
have
different slopes at the level of confidence 100(1-2[alpha])%.
If the slopes
are not statistically distinguishable then they can be
tested to
determine if they are also coincident.
To do this, a common
slope must
next be calculated for all the above data.
Thus, the fifth
step is to
estimate a common slope, [m.sub.c], and a common residual variance,
[S.sub.c] for
the two data sets together. <see equation below>
bsex214b.gif (230x600)

Sixth,
calculate the corresponding common t-value, [t.sub.c]: <see equation 23>
bsex214c.gif (207x600)

As above, if
[t.sub.c] is greater than the t-value for ([n.sub.1]+[n.sub.2]+3) degrees of
freedom at
the desired level of significance, [alpha], then the two lines are
parallel but
statistically distinguishable. If
[t.sub.c] is less than the
t-value then
they are statistically indistinguishable at the level of
confidence
100(1-2[alpha])%.
An idealized
field study will be analyzed to illustrate the technique.
The first
week, daily wood weighings are done for each of the eight
families
using their traditional stove. For each
family, the number of
adult
equivalents eating and the fuel consumption per adult equivalent are
calculated
for each day and then averaged over the week.
The second week,
the process
is repeated with the families using improved stove model A;
the third
week with improved stove model B. The
fourth week, the families
again use
their traditional stoves so as to check that the performance is
the same;
that is, to verify that the conditions, weather, wood moisture
content, and
other variables that could affect the stove performance, have
remained the
same during the entire period of testing.
The data are
summarized in
Table 6.
These data
are plotted in Figure 3. Although it is
easy to see that stove
bse3x217.gif (600x600)

A consumes
less fuel than the traditional stove, it is not easy to see any
difference
between stove B and the traditional one.
The first
step is to calculate [bar]X, [bar]Y, [S.sub.xxn], etc.
The results are listed in
Table 7.
The
regression lines are given by (Table 7 and equations 11 to 14 above):
Traditional
stove: Y = -28.6(x-10.25) + 625. R =
-0.84
Model A
stove: Y = -19.4(x-10.25) +
387.5 R = -0.56
Model B
stove: Y = -29.0(x-10.375) +
575. R = -0.89
where Y is
the fuel consumption per person per day, x is the family size
in adult
equivalents, and R is the correlation coefficient.
Clearly,
stove A has a
lower fuel consumption than the others.
However, its change
in fuel
consumption with family size is also significantly different.
To
compare these
stoves, the fuel consumption per person for the average size
of family can
be used. At x = 10. 25, the traditional
stove uses 625
grams/person-day,
stove A uses 387.5 grams/person-day, and stove B uses
578.6
grams/person-day. Because of the strong
correlation between family
size and fuel
consumption usually observed in the field, it is important
that stove
performance be compared on the basis of the same family size.
The
regression lines for the traditional and model B stoves have similar
slopes and
can be compared. Calculating the
residual variance, equation
(16), for
each data set <see equation below>
bsex215a.gif (150x600)

From this the
pooled residual variance is given by [S.sup.2.sub.pr] = 4820.
The
corresponding pooled t-value is <see equation below>
bsex215b.gif (87x600)

From the
t-table, for (8+8-4)-12 degrees of freedom, the 80 percent level
of confidence
([alpha]-10) is (1.356). Thus, the
slopes of these two lines are
statistically
indistinguishable.
Now a common
slope and common sample variance for the two data sets
combined can
be calculated.
[m.sub.c] = 28.8 and [S.sub.c] = 66.7
TABLE 6
Data From A Hypothetical
Field Study
Week 1
Week 2
Week 3
Traditional Stove
Model A
Model B
Equivalent
Fuel per
Equivalent Fuel per
Equivalent
Fuel per
FAMILY
Adults
person-day
Adults person-day
Adults
person-day
A
4 800
4
600
5
800
B
7 700
7
400
6 700
C
9 600
9
500
9 600
D
10 700
10 400
9
500
E
11 700
11
300
11 600
F
11 600
12
400
12 500
G
14 400
14
300
15 500
H
16 500
15
200
16 400
TABLE 7
Regression Analysis Of
Hypothetical Field Study
Traditional
Stove A
Stove B
Stove
[bar]X
10.25
10.25
10.375
[bar]Y
625.
387.5
575.
[S.sub.xxn]
99.5
91.5
107.875
[S.sub.yyn]
115,000.
108,750.
115,000.
[S.sub.xyn]
-2850.
-1775.
-3125.
The
corresponding t-value is <see equation below>
bsex216.gif (167x600)

For
(8+8-3)=13 degrees of freedom, the t-table gives a t-value of 1.35 for
the
100(1-2[alpha])=80 percent confidence level ([alpha]=10) and 1.771 for the 90
percent
confidence level ([alpha]=5). Thus,
1.771 > [t.sub.c]-1.39 > 1.35, that is,
there is
greater than an eighty percent chance, but less than 90 percent,
that these
two stoves have a different level of performance (although it
has already
been shown that the change in their performance with family
size, i.e.
the slope of their regression lines, is the same).
The beat
estimate of
their relative performance vas given above for the family size
of 10.25,
that is 625 grams/person-day versus 578.6 grams/person-day or
stove B uses
7.5 percent less fuel than the traditional stove.
In analyzing
real field data there are numerous complications.
The fuel
consumption
and/or the numbers of people fed can vary dramatically from
day to day
for an individual family. In this case,
it may be better to do
the linear
regressions or other analyses on the daily data from all the
families
combined rather than first averaging it over the time period
(week) for
each family. The fuel consumption will
often tend to decrease
somewhat with
time as the families become more sensitive to fuel use or
better learn
how to control their stoves. Changes in
weather, such as the
beginning or
end of the rainy season, can sometimes dramatically affect
fuel
consumption. This factor, in
particular, could be reduced by
monitoring
the fuel moisture content. The family's
economic status can
also be a
large factor in determining fuel use.
Such factors as these can
often be
accounted for by doing a multiple regression on the data.
Linear
Regression on Two Variables
In many cases
there are two or more variables which determine the system's
response.
The laboratory PHU of a stove might be
determined by both the
channel
height and gap, or the fuel consumption per person might depend on
both the
family size and income, or perhaps on the family size and day of
the test --
the fuel consumption decreasing as the family becomes more
sensitized to
their fuel use. To analyze such cases
the following procedure
is used.
Given n
triplets of observations ([y.sub.1], [x.sub.1i] [x.sub.2i]), the regression
equation
which fits
this data is <see equation below>
bsex218a.gif (600x600)

and the
partial correlation coefficient between [x.sub.1] and y is given by <see
equation below>
bsex218b.gif (600x600)

In the case
where the variables [x.sub.1] and [x.sub.2] have no correlation
([S.sub.x1x2n]=0)
the formulas
above for [m.sub.1] and [m.sub.2] reduce to that for linear regression on a
single
variable. In many cases, however,
[x.sub.1] and [x.sub.2] will not be independent.
For example,
consider the case where [x.sub.1] is the family size, [x.sub.2] is
the family
income, and y is the fuel consumption per person-day.
Both [x.sub.1]
and [x.sub.2]
will affect y. Additionally, however,
families with larger incomes
will
frequently have fewer children. Thus
[x.sub.1] and [x.sub.2] are not independent
in this case.
As a final
worked example, laboratory test data on insulated charcoal
stoves during
the second, simmering phase and listed in Table VI-2 will be
analyzed.
The data is listed in Table 8 with y the
PHU, [x.sub.1] the channel
gap in
millimeters, and [x.sub.2] the channel length in centimeters.
The PHU is
extraordinarily
high and is less sensitive to the channel dimensions than
would be
expected from Chapter III for reasons discussed in Chapter VI.
From this
data the sums, sums of squares, and sums of products can be
calculated as
before. The averages and other factors
can then be calculated.
The results
are listed below in Table 9.
bsex219.gif (600x600)

TABLE 8
PHU Data for Charcoal Stoves,
Simmering Phase
Y (PHU)
gap [x.sub.1] (mm.)
length [x.sub.2] (cm.)
57.5
3
5
68.6
3
10
78.4
3
15
50.2
5
5
71.9
5
10
77.3
5
15
48.8
8
5
61.7
8
10
64.9
8
15
From Table 9,
the slopes and partial correlation coefficients are calculated.
[m.sub.1] = -1.997
[R.sub.x1y] = -0.776
[m.sub.2] =
2.1367 [R.sub.x2y] =
0.934
Thus, the
regression equation is given by:
y = 64.4 - 2.0([x.sub.1]-5.3) +
2.1([x.sub.2]-10)
This equation
is the best linear fit possible to the data.
The equation
says, for
example, that decreasing the channel gap from 5.3 to 3.0 mm will
increase the
PHU by about 4.6%; lengthening the channel from 10 to 15 cm.
will increase
the PHU by about 10.5%. As can be seen
from the partial
correlation
coefficients, the fit is quite good between the PHU, y, and
the channel
length, [x.sub.2]. It is not as good
between the PHU, y, and the
channel gap,
[x.sub.1].
There are numerous
other useful statistical techniques as well, such as
regression on
more than two variables, analysis of variance, and many
others.
The interested reader should refer to a
textbook on the subject
for details
(1).
APPENDIX H:
TESTING EQUIPMENT
Useful
instruments in stove design, development, and testing are listed
below.
A very extensive list of manufacturers for
these and other
scientific
instruments is given as reference (1).
o
Flexible metal tape measure: Used to measure
template, stove, and pot
dimensions, etc.
o
Balance: Used for laboratory, controlled
cooking, and field tests. In
the laboratory and controlled cooking tests
a balance with a precision
of [- or +]1 gram is desirable.
The balance capacity should be at least 5 kg
and preferably 10 kg or more.
With higher capacities, the entire stove
can be weighed with charcoal in it, thus
avoiding the complications of
removing the charcoal from the stove,
weighing it, and then restarting
the fire.
The balance should be either a double or triple beam type
balance, or electronic.
The electronic balances have the advantage
of
ease of use and reduced errors in
measurement, but cost considerably
more and are more fragile than the standard
mechanical pan balances.
In field tests, due to the need for
portability, linear spring balances
with a precision of at least [- or +]10
grams are preferred.
No matter what balance is used, its
calibration should be frequently
checked over its entire range by weighing a
set of standard weights.
The balance should also be placed on a
level platform where it will not
be jarred and carefully protected from
dust, extreme heat, and water.
o
Thermometers: Used to measure the water
temperature during lab tests.
Typically, mercury in glass thermometers with a length of 30 to 45 cm
and a range of 0 to 105[degrees]C or
110[degrees]C with a precision of al least [- or +]0.5[degree]C
are most useful.
Alternatively, thermocouples can be used.
o
Thermocouples: Used to measure temperatures
of the water, or of the
stove or hot flue gases.
A wide variety of thermocouple wires and
probes are available for different
temperature ranges. In testing
stoves, type K chromel-alumel thermocouple
wire with high temperature
ceramic or glass insulation is usually
adequate. If a direct temperature
readout meter with a built in electronic
cold junction is not
available, then a digital volt meter that
has a resolution of 0.1 mV
and a reference junction, preferably in an
ice bath, will be needed.
For accurate measurements, the test
junction must be in very good
thermal contact with the temperature being
measured.
Direct readout digital thermometers with a
built in reference can be
very convenient, but the standard probes
supplied with them may reduce
the experimenter's flexibility to make a
wide variety of measurements
as they are often too large and unwieldy to
be easily inserted in the
region of interest -- such as the pot to
wall channel. In this case
the experimenter will want to make a
personal set of thermocouple
probes from standard type K wire.
o
Kilns: Used to measure the moisture content
of wood. "Wet" wood is
collected in the field and placed in air
tight plastic bags and in a
cool location until the moisture test can
be done (Note that many types
of plastics are somewhat permeable -- the
test should be done as soon
as possible).
The wood alone is then weighed and placed in the kiln to
dry at 105[degrees]C until its weight
becomes constant. This can take several
days depending on the size of the
wood. The difference between its
initial and final weights is the moisture
content. Alternatively,
though less precise, an electronic moisture
meter can be used to
estimate the moisture content.
o
Moisture meter: Used to measure the
approximate moisture content of
wood.
It consists of a calibrated four prong probe which is inserted
into the wood.
The meter measures the electrical resistance of the
wood through these probes and from that
gives a readout of the moisture
content.
Such moisture meters can have a reduced accuracy for moisture
contents greater than 25%.
Further, as they only measure the surface
moisture content, they can be seriously in
error for the interior.
o
Bomb calorimeter: Used to measure the
calorific value of the wood or
biomass being used with the stove.
o
Gas analysis: Used to measure the carbon
monoxide and other gases
released by combustion in the stove.
A variety of portable personal
monitors to determine individual exposures
to smoke and suspended
particulates have been developed by the
Resource Systems Institute of
the East-West Center.
Interested readers should contact them
directly.
When
purchasing laboratory or field testing equipment, it is important to
know how
their precision will affect the overall quality of data.
For
such analysis
the following rules can be used (2).
If m
measurements with an apparatus give an estimated average reading and
sample
deviation of [X.sub.m][- or +][S.sub.mx], n measurements with a second
apparatus gives
[Y.sub.n][-
or +][S.sub.ny], and so on; then the sum of such measurements is
given by:
<see equation 1>
bsex222a.gif (167x600)

where a, b,
c, .... are constants; and the product of such
measurements
is <see equation 2>
bsex222b.gif (167x600)

where i,
j,... are exponents. In both these
cases it is assumed that the
variables X,
Y,..., are uncorrelated.
Use of these
formulas is straight-forward. Consider,
for example, the
errors in a
laboratory PHU test if the thermometer has an error of [- or +]1[degree]C
(determined
by repeatedly measuring the temperatures of e.g. boiling water
over a period
of time and then calculating the sample deviation) and the
balance has a
typical error of [- or +]2 grams. Then
from Chapter V, <see equation 3>
bsex223a.gif (167x600)

and with
typical values of [W.sub.i]=5.000 kg; [W.sub.f]=4.700 kg;
[T.sub.i]=30[degrees]C; [T.sub.f]=100[degrees]C;
[M.sub.i]=0.500
kg; [M.sub.f]=0.150 kg; [C.sub.i]=0 kg; [C.sub.f]=0.040 kg; [C.sub.w]=18000
kJ/kg; and
[C.sub.c]=29000
kJ/kg. Inserting these assumed values
along with the errors into
equation (3)
gives <see equation below>
bsex223b.gif (600x600)

or, as a
percentage <see equation below>
bsex223c.gif (70x600)
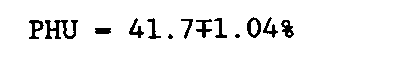
If a balance
with a one gram precision is used instead, then the same
procedure can
be used to find <see equation below>
bsex223d.gif (97x600)

If, in
addition, a thermometer with a precision of 0.5[degree]C is used, the
error is
further reduced to <see equation below>
bsex223e.gif (78x600)

Thus, by
following a simple procedure such as this (see reference (2) for
a more
rigorous discussion) the effect on data quality of different levels
of precision
in any laboratory instruments can be quantified.
Whether or
not a more
precise and expensive instrument is worthwhile can then be
determined
directly. In some cases it will be
found that the errors due
to a
previously overlooked instrument, such as a $5 thermometer, will far
outweigh the
potential advantage of upgrading another instrument, such as
a balance.
Other factors
that should also be considered include the variability of
the calorific
value and moisture content of the fuel; the effect of the
wind on the
balance; differences in the way personnel handle the fuel,
fire, pots,
and water; and many others. An analysis
should be done of
each of these
factors by first repeating measurements of each over a
period of
time to determine the sample deviation and then performing an
overall error
analysis such as the above.
APPENDIX I:
UNITS AND CONVERSIONS
The
International System of Units (SI) is based on the units listed in
Table 1.
All other quantities are derived from these
seven arbitrarily
chosen units
and various examples are listed in Table 2.
Table 3 lists
bsex225.gif (600x600)

common
prefixes used in the SI system. Table 4
lists some physical
constants in
SI units. Table 5 lists common
conversion factors between
bsex2270.gif (600x600)

the SI system
and other system of units. For a more complete discussion,
the reader
should review references (1,2,3-6) from which the following
materials are
extracted.
TABLE 1
Fundamental Units In the
SI System
Quantity
Name
Symbol
length
meter
m
mass
kilogram
kg
time
second
s
electric current
ampere
A
temperature
kelvin
K
number of particles
(atoms, molecules)
mole
mole
luminous intensity
candela
cd
TABLE 3
Prefixes in the International
System of Units
Multiplier
Symbol Prefix
[10.sup.18]
E
exa
[10.sup.15]
P
peta
[10.sup.12]
T
tera
[10.sup.19]
G
giga
[10.sup.6]
M
mega
[10.sup.3]
k
kilo
[10.sup.2]
h
hecto
[10.sup.1]
da
deka
[10.sup.-1]
d
deci
[10.sup.-2]
c
centi
[10.sup.-3]
m
milli
[10.sup.-6]
[mu]
micro
[10.sup.-9]
n
nano
[10.sup.-12]
p
pico
TABLE 4
Some Fundamental Physical
Constants in the
International System of Units
Quantity
Symbol
Value
Speed of Light in a Vacuum
c
2.99792x[10.sup.8] m/s
Stefan-Boltzmann Constant
[sigma]
5.66961x[10.sup.8] W/[m.sup.2][K.sup.4]
Boltzmann's Constant
K
1.380622x[10.sup.-23] J/K
Avogadro's Constant
[N.sub.A]
6.022169x[10.sup.2 6] 1/kmol
Gas Constant
R
8314.34 J/kmolK
Planck's Constant
h
6.626196x[10.sup.-34] Js
Gravitational Constant
G
6.685x[10.sup.-5] [m.sup.3]/kg[s.sup.2]
Gravitational Acceleration
g
9.8 m/[s.sup.2]
Units and Conversions
APPENDIX J:
INSTITUTIONS
Institutions
active in tropical forestry are listed in reference (1). A
handbook
listing governmental and nongovernmental natural resource management,
environmental
and related organizations is cited as reference (2).
A number of
other institutions involved in biomass energy research and
development
are given in (3). Below are listed institutions involved with
fuel
efficient stove development and dissemination.
Although many of the
larger
organizations such as USAID, the United Nations, and the World Bank
are involved
in stove projects in a variety of countries, only primary
addresses are
listed. This is neither a complete
listing nor a listing of
the most
important groups and should not be construed as such.
It is
simply a
partial listing of institutions as were available at Press-Time.
Apologies go
to all those who have been inadvertently omitted; and they
are requested
to notify the author so that they may be included in future
listings of
active institutions. For additional
information, readers
should also
contact the Foundation for Woodstove Dissemination.
ACEEE
(American Council for an Energy Efficient Economy), 1001 Connecticut
Ave., N.W.
suite 535, Washington, D.C. 20036 USA. (attn: Howard Geller)
ADEREM
(Association pour le Developpement des Energies Renouvelables en
Mauritanie)
B.P. 6174, Nouakchott, Mauritania.
AIDR
(Association Internationale de Developpement Rurale), 20 rue de
Commerce,
Boite 9, B-1040, Brussels, Belgium.
ARD
(Associates in Rural Development), 72 Hungerford Terr., Burlington,
Vt. 05401,
USA.
ASTRA (Centre
for the Application of Science and Technology to Rural
Areas),
Indian Institute of Science, Bangalore, India 560-012.
ATI
(Appropriate Technology International), 1724 Massachusetts Avenue,
N.W.,
Washington, D.C. 20036, USA.
ATOL
(Appropriate Technology for Developing Countries), Blijde Irkomstraat
9, 3000
Leuven, Belgium.
Africare,
1601 Connecticut Avenue, N.W., Washington, D.C., USA.
Appropriate
Technology Development Institute, P.O. Box 793, Lae, Papua New
Guinea.
Aprovecho
Institute, 442 Monroe Street, Eugene, Oregon 97402, USA.
Association
Bois de Feu, 73 Avenue Corot, 13013 Marseille, France.
Bellerive
Foundation, Case Postale 6, 1211 Geneva 3, Switzerland.
Beijer
Institute, The Royal Swedish Academy of Science, Box 50005,
S104-05,
Stockholm, Sweden; and Scandinavian Institute of African Studies,
Bohuslaningens,
AB, Uddevalla, Sweden.
BioEnergy
Users Network, c/o International Institute for Energy and
Development,
1717 Massachusetts Ave. N.W., Washington, D.D. 20036. (attn:
Albert
Binger)/P.O. Box 1660, San Jose, Costa Rica. (attn: Alvaro Unana).
Brace
Research Institute, McDonald College of McGill University, P.O. Box
255, ste.
Anne de Bellevue, Quebec, Canada H9X 1CO.
CDI (Centro
de Desarrollo Industrial), A.P. 1626, Tegucigalpa, Honduras.
CEAER,
Universite du Rwanda, Butare, Rwanda; (attn: Prosper Mpawenayo)
CEES (Center
for Energy and Environmental Studies); Princeton University,
Princeton,
New Jersey, 08544. USA. (attn: Sam Baldwin, Gautam Dutt, Eric
Larson, Bob
Williams).
CERER (Centre
d'Etudes et de Recherches sur les Energies Renouvelables)
Universite de
Dakar, B.P. 476, Dakar, Senegal.
CEMAT (Center
for Mesoamerican Studies on Appropriate Technology), P.O.
Box 1160
Guatemala.
CICON (Centro
de Investigaciones de Ingenieria), Ciudad Universitaria,
Zona 12,
Guatemala.
CILSS (Comite
Permanent Inter-etats de Lutte Contre la Secheresse dans le
Sahel),
Equipe Ecologie-Forets, B.P. 7049, Ouagadougou, Burkina Faso.
CISIR (Ceylon
Institute for Scientific and Industrial Research), P.O. Box
787, 363
Bauddhaloka Mawatha, Colombo 7, Sri Lanka.
CORT
(Consortium on Rural Technology), E-350, Nirman Vihar, Delhi 11092
India
CRES (Centre
Regional Energie Solaire), B.P. 1872, Bamako, Mali.
CWS (Church
World Service), B.P. 11624, Niamey, Niger (attn: Ralph Royer);
B.P. 3822
Dakar, Senegal (attn: Lionel Derenoncourt).
Center for
Development Technology, Department of Technology and Human
Affairs,
Washington University, St. Louis, Missouri 63130 USA. (attn:
Robert P.
Morgan)
Center for
the Study of Energy and Natural Resources, Universidad Catolica
Madre Y
Maestra, Santiago de los Caballeros, Dominican Republic
Center for
Energy Research, National Office for Scientific and Technical
Research,
Yaounde, Cameroon.
Centre
National des Energies Alternatives, BP 199, Nouakchott, Mauritania.
Centre
National de Productivite, B.P. 811 Conakry, Guinea.
Institutions
Centre
Technique Forestier Tropical, 45 bis, avenue de la Belle Gabrielle,
94130
Nogent-sur-Marne, France.
Chemical
Engineering Department, Bangladesh University of Science and
Technology,
Dacca 2, Bangladesh.
DHV Consulting
Engineers, P.O. Box 85, 3800 AB Amersfoot, The Netherlands
(attn:
Gerhard van de Rhoer).
Department of
Community Development, Banjul, The Gambia (attn: Bai
Bojang);
Department of Forestry, No. 5 Marina, Banjul, The Gambia (attn:
Bymaas Taal).
Dian Desa,
P.O. Box 19 Bulaksumur, Yogyakarta Dij, Indonesia.
Directorate
of Research, N.W.F.P. University of Engineering and Technology,
Peshawar,
Pakistan (attn: I.H. Shah).
EEC (European
Economic Community); Directorate General for Energy; Commission
of the
European Communities; Rue de la Loi 200; B1049 Brussels,
Belgium.
E/DI (Energy
Development International), 1015 18th Street, N.W. Suite 802,
Washington,
D.C. 20036. USA.
Earthscan, 10
Percy Street, London W1P ODR, United Kingdom.
East-West
Center, Resource Systems Institute, 1777 East-West Road,
Honolulu,
Hawaii, 96848 USA. Contact: Kirk Smith
Eglise
Lutherienne Malgache, Foibe Fampandrosoana, Dept. of Development,
Antsirabe,
Madagascar.
Energy
Research Group, Carleton University, C.J. MacKenzie Building, Room
218, Colonel
By Drive, Ottawa K1S 5B6 Canada.
Energy
Research Institute, University of Cape Town, Private Bag, Rondebosch
7700, South
Africa.
Energy
Resources Group, University of California, Rm. 100, Bldg. T-4,
Berkeley,
California 94720, USA.
Energy Unit,
Ministry of Agriculture, Box 30134, Lilongwe 3 Malawi.
Environmental
Studies Center, Wright State University, Dayton, Ohio 45435
USA. (attn:
Timothy Wood).
FUNDAEC,
Apartado Aereo 6555, Cali, Colombia.
Forestry
Research Institute of Malawi, P.O. Box 270, Zomba, Malawi
Foundation
for Woodstove Dissemination, Korte Jansstraat 7, 3512 GM
Uttrecht, the
Netherlands. (attn: Ad Hordijk)
GATE (German
Appropriate Technology Exchange) P.O. Box 5180. D6236
Eschborn 1,
West Germany; See GTZ.
GRET (Groupe
de Recherche et d'Echanges Technologies), 34 rue Dumont
d'Urville
75116 Paris, France.
GRUEA (Groupe
de Recherche des Utilisations des Energies Alternatives),
Universite de
Burundi, Faculte des Sciences, B.P. 2700, Burundi
GTA (Grupo
Tecnologia Appropriada) Apartado 8046, Panama 7, Panama.
GTZ,
(Deutsche Geseltschaft fur Technische Zusammerenarbeit), Postfach
5180,
Dag-Hammerskjoldweg 1, D-6236 Eschborn 1, West Germany.
German
Forestry Mission (Mission Forrestiere Allemand), BP 13, Ouagadougou,
Burkina Faso.
Guangzhou
Institute of Energy Conversion, Chinese Academy of Sciences, 81
Martyr's
Road, Guangzhou, Canton, People's Republic of China
IBE (Institut
Burkinabe de l'Energie), BP 7047, Ouagadougou, Burkina Faso
ICAITI, Apartado
Postal 1552, Avenida la Reforma 4-47, Zona 10, Guatemala,
Guatemala
(attn: Marco Augusto Recinos).
IDRC
(International Development Research Center), Box 8500, Ottawa,
Ontario,
Canada K1G 3H9
IIED,
International Institute for Energy and Development, 1717 Massachusetts
Avenue, N.W.,
Washington, D.C. 20036.
INE
(Instituto Nacional de Energia), Italia No. 438 y mariana de jesus,
Quito,
Ecuador
ITDG
(Intermediate Technology Development Group), 9 King Street, London
WC2E 8HN,
United Kingdon (attn: Yvonne Shanahan).
IT Power
(Intermediate Technology Power, Ltd.), Mortimer Hill, Mortimer,
Reading,
Berkshire, RG7 3PG United Kingdom.
IUFRO
(Fuelwood Production Information Network), A-1131, Vienna, Austria.
(attn: Oscar
Fugalli).
Institut du
Sahel, BP 1530, Bamako, Mali
Instituto de
Energia, Academy of Sciences, Casilla 5279, La Paz, Bolivia.
Instituto
Mexicano de Tecnologias Apropriadas SC, Farallones 60-B, Col.
Acueducto de
Gpe., C.P. 07270, Apdo. Postal 63-254, 02000 Mexico, D.F.
Institutions
Instituto
Nacional de Investigacao Tecnologica, C.P.
185, Praia, Cape
Verde.
Instituto
Tecnologico de Costa Rica, Centro de Informacion Technologica,
Apartado 159,
Cartago, Costa Rica.
International
Rice Research Institute, P.O. Box 933, Manila, Philippines.
KENGO (Kenya
Energy Non-Governmental Organization Association),
P.O. Box
48197,
Nairobi.
Kenya
National Council for Science and Technology, Box 30623, Nairobi.
LESO
(Laboratoire d'Energie Solaire), B.P. 134, Bamako, Mali.
Laboratorium
voor Koeltechnik en Klimaatreling Katholieke Universiteit,
3030
Heverlee, Belgium (attn: G. de Lepeleire).
Mazingiri
Institute, P.O. Box 14550, Nairobi, Kenya.
Ministry of
Energy, P.O. Box 2256, Government Buildings, Suva, Fiji (attn:
Jerry
Richolson).
Ministry of
Energy, Government of Kenya, P.O. Box 30582, Nairobi, Kenya.
Ministry of
Foreign Affairs, Section For Research and Technology, P.O.
Box 20061,
2500 EB The Hague, The Netherlands.
(attn: Joan Boer)
Ministry of
Science and Technology, Department of Non-Conventional Energy
Sources,
Government of India, C.G.O. Complex Block No.14, Lodi Road, New
Delhi, 110
003.
NAS/BOSTID;
National Academy of Sciences, Board on Science and Technology
in
Development, Room JH-213, 2101 Constitution Avenue, N.W., Washington,
D.C. 20418
USA.
OECD Club du
Sahel, 2 rue Andre Pascal, 75775 Paris Cedex 16 France.
OLADE (Latin
American Energy Organization), Casilla 119-A, Quito, Ecuador.
ONERSOL
(Office de 1'Energie Solaire), B.P. 621, Niger.
OXFAM-America,
Inc. 115 Broadway, Boston Massachusetts, USA.
Peace Corps,
806 Connecticut Avenue, N.W. Washington, D.C. USA.
Projet
National Foyers Ameliores, B.P. 296, Niamey, Niger, (attn: Issaka
Hassane).
RECAST
(Research Center for Applied Science and Technology) Tribhuvan
University,
Kirtipur, Kathmandu, Nepal.
RETAIN,
(Rural Energy Technology and Innovation Network) Science Policy
Research
Unit, Mantell Building, University of Sussex, Falmer, Brighton
BN1 9RF,
United Kingdom.
Rural
Industries Innovation Center, Box 138, Kanye, Botswana.
Service Des
Foyers Ameliores, Jeunesse Canada Monde, 4824 Cote des Neiges,
Montreal,
Quebec, Canada H3V 1G4.
SKAT (Swiss
Center for Appropriate Technology), Varnbuelstr. 14, Ch-9000
St. Gallen,
Switzerland.
SIDA (Swedish
International Development Authority), Birgir Jaris Gatan 61,
S-10525
Stockholm, Sweden.
Sarvodaya
Institute, Palletalawinna, Katugastota, Kandy, Sri Lanka.
Service
Nationale Projet Foyers Ameliores, Ministere de 1'Environnement et
Tourisme,
B.P.14, Ouagadougou, Burkina Faso.
Silveira
House, P.O. Box 545, Harare, Zimbabwe.
Societe de
Vulgarisation du Foyer Ameliore, 985 Hotel de Ville, Montreal,
Quebec, H2X
3A4, Canada.
Somali
National Committee for Alternative Energy, c/o The Foundry, P.O.
Box 1411,
Mogadishu, Somalia (attn: Ali Dahir).
TATA Energy
Research Institute, Bombay House, 24 Homi Mody Street, Bombay
400-023.
TERI Field
Research Unit, c/o Sri Aurobinda Ashram, Pondicherry 65002
India (attn:
C.L. Gupta).
TOOL,
Stichting TOOL, Mauriskade 61a, Amsterdam, The Netherlands.
UNDP (United
Nations Development Program), one United Nations Plaza, New
York, N.Y.
10017
UNIDO (United
Nations Industrial Development Organization), Lerchen Felder
Strasse 1,
P.O. Box 707, A-1070 Vienna, Austria.
UNFAO (United
Nations Food and Agriculture Organization), Via delle Termi
di Caracalla,
0100 Roma, Italy
UNEP (United
Nations Environment Program), P.O. Box 30522, Nairobi, Kenya.
UNICEF:
Eastern Africa Regional Office, P.O. Box 44145, Nairobi, Kenya.
Universidad
Nacional Autonoma De Mexico, Facultad de Ciencias, Departemento
de Fisica
(3er piso) Ciudad Universitaria 04510, Mexico, D.F. (attn:
Marco A.
Martinez Negrete)
USAID Office
of Policy and Planning, Room 3887, Washington, D.C. 20523 USA
USAID Office
of Energy, DS/ST Room 306 SA-18, Washington, D.C. 20523, USA
USAID Office
of the Sahel, AFR/SFWA Room 3491, Washington, D.C. 20523 USA
University of
Dar Es Salaam, Forestry School, P.O. Box 643, Morogoro,
Tanzania,
(attn: R.C. Ishengoma); Faculty of' Engineering, P.O. Box 35169
Dar Es
Salaam, Tanzania (attn: Simon Nkonoki).
University of
Khartoum, c/o DSRC, P.O. Box 321, Khartoum, Sudan (attn:
Edwin
Hunley).
VITA
(Volunteers in Technical Assistance), 1815 North Lynn Street, Suite
200, P.O. Box
12438, Arlington, Virginia 22209-8438 USA.
Village
Industries Program, P.O. Box 464, Gaborone, Botswana.
Village
Industry Service, P.O. Box 35500, Lusaka, Zambia
Volunteers in
Asia, Box 4543, Stanford, CA 94305 USA
Wood Stove
Group, T.H.E. Eindhoven, University of Technology, W&S, P.O.
Box 513, 5600
MB Eindhoven, The Netherlands.
World Bank,
Science and Technology Unit, Room E1036, 1818 H Street, N.W.,
Washington,
D.C. 20433, USA.
World Bank,
Energy Department, Room D434, 1818 H Street, N.W., Washington,
D.C. 20433,
USA.
World Bank,
Energy Assessment Division, Room D446, 1818 H Street, N.W.,
Washington,
D.C. 20433, USA.
World
Environment Center, 605 Third Avenue, 17th Floor, New York, N.Y.
10158 USA.
World
Resources Institute; 1735 New York Avenue, N.W., Washington, D.C.
20006.
INSTITUTIONS
BY COUNTRY
Austria:
IUFRO; UNIDO
Bangladesh:
Chemical Engineering Department
Belgium:
ATOL; AIDR; EEC; Laboratorium voor Koeltechnik en Klimaatreling
Bolivia:
Instituto de Energia
Botswana:
Rural Industries Innovation Center; Village Industries Program
Burkina Faso:
CILSS; IBE; Service Nationale Projet Foyers Ameliores
Burundi:
CRUEA
Cameroon:
Center for Energy Research
Canada: Brace
Research Institute; Energy Research Group; IDRC; Service Des
Foyers Ameliores; Societe de Vulgarisation
du Foyer Ameliore.
Cape Verde:
Instituto Nacional de Investigacao Tecnologia
China:
Guangzhou Institute of Energy Conversion
Colombia:
FUNDAEC
Costa Rica:
BioEnergy Users Network; Instituto Tecnologico de Costa Rica
Dominican
Republic: Center for the Study of Energy and Natural Resources
Ecuador: INE;
OLADE
Fiji:
Ministry of Energy
France:
Association Bois de Feu; Centre Technique Forestier Tropical;
GRET; OECD Club du Sahel;
Gambia:
Department of Community Development
Germany:
GATE; German Forestry Mission; GTZ
Guatemala:
CEMAT; CICON; ICAITI
Guinea:
Centre National de Productivite
Honduras: CDI
India: ASTRA,
CORT; Ministry of Science and Technology; TATA Energy
Research Institute; TERI Field Research
Institute
Indonesia:
Dian Desa
Italy: UNFAO
Kenya: KENGO;
Kenya National Council for Science and Technology; Mazingiri
Institute; UNEP; UNICEF
Madagascar:
Eglise Lutherienne Malgache
Malawi:
Energy Unit; Forestry Research Institute
Mali: CRES;
Institut du Sahel; LESO
Mauritania:
ADEREM; Centre National des Energies Alternatives
Mexico:
Instituto Mexicano de Tecnologias Apropriadas; Universidad
Nacional Autonoma De Mexico
Nepal: RECAST
Netherlands:
DHV Consulting Engineers; Foundation for Woodstove Dissemination;
Ministry of Foreign Affairs; TOOL; Wood
Stove Group
New Guinea:
Appropriate Technology Development Institute
Niger: CWS;
ONERSOL; Projet National Foyers Ameliores
Pakistan:
Directorate of Research
Panama: GTA
Philippines:
International Rice Research Institute
Rwanda: CEAER
Senegal:
CERER; CWS
Somalia:
Somali National Committee for Alternative Energy
South Africa:
Energy Research Institute
Sri Lanka:
CISIR; Sarvodaya
Sudan:
University of Khartoum
Sweden:
Beijer Institute; SIDA
Switzlerland:
Bellerive Foundation; SKAT
Tanzania:
University of Dar Es Salaam
United
Kingdom: Earthscan; ITDG; IT Power; RETAIN
United States
of America: Africare; ACEEE; ATI; Aprovecho; ARD; BioEnergy
Users Network; Center for Development
Technology; CEES; East-West
Center; E/DI; Energy Resources Group;
Environmental Studies Center;
IIED; NAS BOSTID; Oxfam; Peace Corps; UNDP;
USAID; Volunteers In Asia;
VITA; World Bank; World Environment Center;
World Resources Institute
Zambia:
Village Industry Service
Zimbabwe:
Silveira House
NOTES, REFERENCES, AND
FURTHER READING
Chapter I
1.
Baldwin, Sanuel F., Domestic Energy For
Developing Countries: Options
and Opportunities, forthcoming.
2.
Joseph, S.D., Y.H. Shanahan, and W. Stewart,
The Stove Project Manual:
Planning and Implementation, Intermediate
Technology Publications, 9
King Street, London WC2E 8HW, U.K., 1985.
Chapter II
1.
Sagan, Carl, Owen B. Toon and James B.
Pollack. "Anthropogenic Albedo
Changes and the Earth's Climate",
Science Vol. 206, 1979, pp. 1363-1368.
2.
Eckholm, Erik P., Losing Ground:
Environmental Stress and World Food
Prospects, W.W. Norton and Company, NY, 1976,
223 pp.
3.
Perlin, John and Boromir Jordan,
"Running Out -- 4200 Years of Wood
Shortages", Coevolution Quarterly,
Spring 1983, pp. 18-25.
4.
UNFAO, Tropical Forest Resources, Forestry
Paper No. 30, United
Nations Food and Agriculture Organization,
Rome, 1982, 106 pp.
5.
Technologies to Sustain Tropical Forest
Resources, March 1984, 344
pp.; Sustaining Tropical Forest Resources;
U.S. and International
Institutions. Background paper #2, May
1983; and Sustaining Tropical
Forest Resources:
Reforestation of Degraded Lands.
Background paper
#1, May 1983.
Congressional Office of Technology Assessment; U.S.
Government Printing Office, Washington,
D.C.
6.
"Fuelwood and Charcoal, Report of the
Technical Panel", Second
Session, United Nations (A/CONF.100/PC/34) February 25, 1981.
7.
The Global 2000 Report to the President,
Volume 2, Council on Environmental
Quality and the Department of State, US
Government Printing
Office, Washington, D.C., 1980.
8.
Arungu-Olende, Shem.
"Rural Energy," Natural Resources
Forum, Volume
8, 1984, pp. 117-126.
9.
Dunkerley, Joy; Ramsay, William; Gordon,
Lincoln; and Cecelski,
Elizabeth.
Energy Strategies for Developing Countries, Resources for
the Future, Johns Hopkins University
Press, Baltimore, 1981, 265 pp.
10.
Hall, D.O. "Solar Energy Use Through
Biology -- Past, Present and
Future", Solar Energy, Vol.22, 1979,
pp. 307-328.
11.
Hughart, David. Prospects for Traditional
and Non-Conventional Energy
Sources in Developing Countries, World
Bank Staff Working Paper No. 346, 132
pp., July 1979.
12.
Moss, R.P., and Morgan, W.B. Fuelwood and
Rural Energy Production and
Supply in the Humid Tropics, United
Nations University, Tycooly
International Publishing, Ltd., Dublin, 1981.
13.
Earl, D.E. Forest Energy and Economic
Development, Clarendon Press,
Oxford, 1975.
14.
Abe, Fusako.
"Manufacture of Charcoal from Fast Grown Trees" in W.
Ramsey Smith, ed., Energy from Forest
Biomass, New York: Academic
Press, 1982.
15.
Harris, A.C.
"Charcoal Production", Eighth World Forestry Congress,
Jakarta, Indonesia, 1978.
16.
Wegner, K.F., ed. Forestry Handbook, New
York: John Wiley and Sons,
1984, 1335 pp.
17.
Kuusela, K. and Nyyssonen, A.
"Quantifying Forest Energy",
UNASYLVA,
pp. 31-34.
18.
Openshaw, K. "Woodfuel Surveys:
Measurement Problems and Solutions to
these Problems", Stencil No. 799,
Division of Forestry, University of
Dar Es Salaam, Morogoro, Tanzania, July
10, 1980.
19.
Wood Fuel Surveys, UNFAO, Programme for
Forestry for Local Community
Development, GCP/INT/365/SWE, Rome, 1983,
202 pp.
20.
Hall, D.O.; Barnard, G.W.; and Koss, P.A.
Biomass for Energy in the
Developing Countries, Pergamon Press,
Oxford, 1982, 212 pp.
21.
Nkonoki, Simon and Sorensen, Bent. "A
Rural Energy Study in Tanzania:
The Case of Bundilya Village,"
Natural Resources Forum, Vol. 8, No. 1,
1984, pp. 51-62.
22.
Singh, J.S.; Pandey, Uma; and Tivari, A.K.
"Man and Forests: A Central
Himalayan Case Study", Ambio, Vol.
12, No. 2, 1984, pp. 80-87.
23.
Revelle, Roger. "Energy Use in
India", Science, Volume 192, 1976, pp.
969-975.
24.
O'Keefe, Phil, Paul Raskin, and Steve
Bernow, eds. Energy and Development
in Kenya: Opportunities and Constraints,
Beijer Institute and
Scandinavian Institute of African
Studies, 1984, Bohuslaningens, AB,
Uddevalla, Sweden, 1984.
25.
Keita, M.N. Les Disponibilites de Bois de
Feu en Region Sahelienne de
l'Afrigue Occidentale -- Situation at
Perspectives, Rome: UNFAO, 1982.
26.
Alio, Hamadil.
Firewood Shortage in the Sahel Countries: A Niger Case
Study, M.Sc. Thesis, University of
Arizona, 1984.
27.
CILSS Equipe Regional Ecologio-Forets.
"Quantification des Besoins en
Bois des Pays Saheliens: Une Analyse des
Bilans/Programmes", Comite
Permanent Interetat de Lutte contre la
Secheresse dans le Sahel",
Reunion de Banjul, October 18-22, 1982.
28.
Clement, Jean.
Estimation des Volumes et de la Productivite des
Formations Mixtes Forestieres et
Graminennes Tropicales, Centre
Technique Forestier Tropical, 45 bis,
avenue de la Belle Gabrielle,
94130 Nogent-sur- Marne, France.
29.
See references (1-4,6,9,17-21); reference
(17) is a particularly
useful review of the literature.
30.
Islam, M. Nunil; Morse, Richard; and
Soesastro, M. Hadi, eds. Rural
Energy to Meet Development Needs:
Asian Village Approaches, Boulder,
Colorado, and London: Westview Press,
1984, 561 pp.
31.
O'Keefe, Phil, and Kristoferson, Lars.
"The Uncertain Energy Path -- Energy
and Third World Development", Ambio,
V.13, 1984, pp. 168-170.
32.
Munslow, Barry; O'Keefe, Phil; Parkhurst,
Donna; and Philips, Peter.
"Energy and Development on the
African East Coast", Ambio, Volume 12,
No. 6, 1983, pp. 332-337.
33.
Dunkerley, Joy. "Patterns of Energy
Consumption by the Rural and Urban
Poor in Developing Countries",
Natural Resources Forum, Volume 3,
1979, pp. 349-363.
34.
Arnold, J.E.M. "Wood Energy and Rural
Communities", Natural Resources
Forum, Volume 3, 1979, pp. 229-252.
35.
Goldemberg, Jose. "Energy Problems in
Latin America", Science, Volume
223, 1984, pp. 1357-1362.
36.
Dunkerley, Joy, and Rassay, William.
"Energy and the Oil-Importing
Developing Countries", Science,
Volume 216, 1982. pp. 590-595.
37.
O'Keefe, Phil.
"Fuel for the People:
Fuelwood in the Third World",
Ambio, Volume 12, 1983, pp. 15-17.
38.
Earl, Derek.
"A Renewable Source of Fuel", UNASYLVA, Volume 27, No.
110, 1975, pp. 21-26.
39.
Mnzava, E.M.
"Village Industries vs. Savannah Forests", UNASYLVA,
Volume 33, No. 131, 1981, pp. 24-29.
40.
Arnold, J.E.M. and Jongma, Jules.
"Fuelwood and Charcoal in Developing
Countries", UNASYLVA, Vol. 29(118),
1978. pp. 2-9.
41.
Bhagavan, M.R. "The Woodfuel Crisis in
the SADCC Countries", Ambio,
Volume 13, No. 1, 1984, pp. 25-27.
42.
Hinrichson, Don.
"Fuelwood and Charcoal: The Other Energy Crisis",
Ambio, Volume 10, No. 5, 1981, pp.
234-235.
43.
Goldemberg, Jose; Hukai, Roberto Y.; et al.
A Country Study -- Brazil,
A Study on End-Use Energy Strategy,
Global Workshop on End-Use
Oriented Energy, Sao Paulo, Brazil, June
4-15, 1984.
44.
Servin, Jesus Cervantes; Negrete, Marco
Antonio Martinez; Cerutti,
Omar Masera; and Estrada, Fernando
Shutz. End-Use Oriented Energy
Strategies for Mexico, Global Workshop on
End-Use Oriented Energy
Strategies, Sao Paulo, Brazil, June 4-15,
1984.
45.
Reddy, Amulya Kumar N.; and Reddy, B.
Sudhakar. Energy in a Stratified
Society -- A Case Study of Firewood in
Bangalore, Indian Institute of
Science, Bangalore 560 012, July 1982.
46.
Shrestha, Kedar Lal.
Energy Strategies in Nepal and Technological
Options, Research Center for Applied
Science and Technology, Tribhuvan
University, Nepal, End-Use Oriented
Global Energy Workshop, Sao Paulo,
Brazil, June 1984.
47.
Mwandosya, M.J. and Luhanga, M.L. Energy
Demand Structures in Rural
Tanzania, Department of Electrical
Engineering, University of Dar-Es- Salaam,
P.O. Box 35131, Dar-Es- Salaam, Tanzania.
48.
Balanco Energetico Nacional, Republica
Federativa do Brazil, Ministerio
des Mines E Energia, Bloco J,
75.056-Brasilia-DF, 1983.
49.
Mwandosya, M.J. and Luhanga, M.L.P. Energy
Use Patterns in Tanzania,
Short form: Center for Energy and
Environmental Studies Report No.
180, Princeton University, Princeton,
N.J., Feb. 1985. Full length:
Department of Electrical Engineering,
University of Dar Es Salaam, Dar
Es Salaam, Tanzania, Draft, 1984, 240 pp.
50.
Ravindranath, N.H.; Nagaraju, S.M.;
Somashekar, H.I.; Channeswarappa,
A.; Balakrishna, M.; Balachandran, B.N.;
and Reddy, Amulya Kumar N.
"An Indian Village Agricultural
Ecosystem -- Case Study of Ungra
Village, Part I:
Main Observations", Biomass, Volume 1,
No. 1,
September 1981, pp. 61-76.
51.
Reddy, Amulya Kumar N. "An Indian
Village Agricultural Ecosystem -- Case
Study of Ungra Village, Part II:
Discussion", Biomass, Volume 1,
No. 1, September 1981, pp. 77-88.
52.
Makhijani, Arjum and Poole, Alan. Energy and
Agriculture in the Third
World, Ballinger Publishing Company,
Cambridge, Mass., 1975, 168 pp.
53.
Tiwari, K.M. "Fuelwood -- Present and
Future with Special Reference to
Conditions in Developing Countries",
in Energy from Biomass, 2nd
International Conference on Biomass, A.
Strub, P. Chartier and G.
Schleser, eds., London: Applied Science
Publishers, 1982.
54.
Hall, D.O., and Moss, Patricia.
"Biomass for Energy in Developing
Countries." Geojournal, Vol. 7.1,
1983, pp. 5-14.
55.
Cecelski, E., "Energy Needs, Tasks, and
Resources in the Sahel:
Relevance to Woodstove Programs,"
Geojournal, Vol. 7.1, 1983, pp.
15-23.
56.
Hyman, E.L. "The Demand for Woodfuels
by Cottage Industries in the
Province of Ilocos Norte,
Philippines," Energy, Vol. 9, pp.
1-13,
1984.
57.
Zhu, H., Brambley, M.R. and Morgan, R.P.,
"Household Energy Consumption
In The People's Republic of China",
Energy V.8, pp 763-774, 1983.
58.
Down, S.
"Household Energy Consumption In West Sumatra. Implications
for Policy Makers", Energy, Vol. 8
pp 821-833, 1983.
59.
Mnzava, E. M.
"Fuelwood and Charcoal in Africa", in Energy from
Biomass, First International Conference
on Biomass, Brighton, East
Sussex; W. Paley, P. Chartier, D.O. Hall,
ads., London: Applied
Science Publishers, Ltd., 1980.
60.
Chauvin, Henri. "When an African City
Runs Out of Fuel", UNASYLVA,
Vol. 33 (133) pp. 11-20., 1981
61.
Boureima, Issoufou and Gilles De
Chambre. "Rapport sur l'evaluation
du programme foyers ameliores",
Niamey, Niger: Association des Femmes
du Niger and Church World Service,
November 1982.
62.
Sassin, Wolfgang, "Energy,"
Scientific American, Sept. 1980, p. 119.
63.
Prasad, K. Krishna. Cooking Energy, Workshop
on End-Use Focused Global
Energy Strategy, Princeton University,
Princeton, New Jersey, April
21-29, 1982.
64.
Williams, Robert H. Potential Roles for
Bioenergy in an Energy
Efficient World, Princeton University
center for Energy and Environmental
Studies, Report No. 183, February 1985;
Workshop on Biomass
Energy Systems, Airlie House, Virginia,
January 29-February 1, 1985.
65.
United Nations, Yearbook of World Energy
Statistics, 1981, New York:
United Nations, 1983.
66.
Booth, H.E.
"Realities of Making Charcoal", UNASYLVA, Volume 33, No.
131, 1981, pp. 37-38.
67.
FLORASA, Man-Made Forests for Wood and
Charcoal in Brazil, Minas Gerais,
Brazil: Florestal Acesita, S.A., Belo
Horizonte, Oct.1983, 53 pp.
68.
Uhart, E. Preliminary Charcoal Survey in
Ethiopia, U.N. Economic
Commission for Africa, FAO Forest
Industries Advisory for Africa, Doc.
M75-1122, 1975, 30 pp.
69.
Karch, G.E. Calrbonization: Final Technical
Report of Forest Energy
Specialist, UNFAO, SEN/78/002, 1980.
70.
Wood, T.S. Report on Domestic Energy Use for
Cooking (Energy Assessment
Mission, Ethiopia), Washington, D.C.:
World Bank, 1983, 33 pp.
71.
Wartluft, Jeffrey.
"Team Compares Charcoal Production Methods", VITA
News, October 1983, pp.8-11. Wartluft,
Jeffrey L. and White, Stedford.
Comparing Simple Charcoal Production
Technologies for the Caribbean,
Arlington, Virginia: VITA, March 1984.
72.
Charcoal Production Improvement For Rural
Development In Thailand,
Forest Products Research Division, Royal
Forest Department, Ministry
of Agriculture and Cooperatives, for the
National Energy Administration,
Ministry of Science, Technology, and
Energy under the Renewable
Nonconventional Energy Project, Royal Thai
Government and U.S. Agency
For International Development, Bangkok,
Thailand, 1984, 163 pp.
73.
Rose, A.B., Energy-Intensity and Related
Parameters of Selected
Transportation Modes:
Freight Movements, Oak Ridge National
Laboratory,
ORNL 5554, June 1979, 135 pp.
74.
Bonney, R.S.P. and Stevens, N.F. Vehicle
Operating Costs on Bituminous,
Gravel, and Earth Roads in East and
Central Africa, Road Research
Technical Paper No. 76, Road Research
Laboratory, Ministry of Transport,
London, 1967.
75.
Truck Operating Characteristics in the
Sudan, Transport and Communications
Section, Ministry of National Planning,
Khartoum, June 1978.
76.
Wardle, Philip and Palmieri, Massimo.
"What Does Fuelwood Really
Cost?", UNASYLVA, Volume 33, No.
131, 1981, pp. 20-23.
77.
Foley, Gerald, and van Buren, Ariane.
"Substitutes for Wood",
UNASYLVA, Volume 32, No. 130, pp. 11-24.
78.
Weber, F., Economic and Ecologic Criteria of
Forestry/Conservation
Projects in the Sahel, International
Resource Development and Conservation
Services, Boise, Idaho, 1977.
79.
Baldwin, Sam. Technical Notes for the
Senegalese `Ban Ak Suuf'
(Improved Stove) Program.
CERER/CILSS/VITA, July 1983, revised
December 1983. Available from VITA.
80.
Yameogo, Georges; Bussman, Paul; Simonis,
Philippe; and Baldwin, Sam.
Comparison of Improved Stoves; Lab.
Controlled Cooking, and Family
Compound Tests.
IVE/THE Eindhoven/GTZ/CILSS/VITA, May 1983, Available
from VITA.
See also, Yameogo, Georges; Evaluation
des differents Prototypes de
Foyers Ameliores Existants en Haute
Volta; Universite de Ouagadougou,
Institut Superieur Polytechnique; Mamoire
de fin d'Etudes. Juin 1983
L'Institut Voltaique de L'Energie,
rapport No.1, Etat de Developpment
Technigue des Foyers Ameliores en Haute
Volta, Ouagadougou, April 1983
81.
Smil, Vaclav.
"Deforestation in China", Ambio, Volume 12, No. 5,
1983,
pp. 226-231.
82.
Brown, Lester R. ; Chandler, William;
Flavin, Christopher; Postel,
Sandra; Storke, Linda; and Wolf,
Edward. State of the World 1984.
Worldwatch Insitute, New York:
W.W. Norton and Company, 1984.
83.
Jackson, Peter.
"The Tragedy of our Tropical Rainforests", Ambio,
Volume 12, No. 5, 1983, pp. 252-254.
84.
Steinlin, Hans Jurg.
"Monitoring the World's Tropical
Forest",
UNASYLVA, Volume 34, No. 137, 1982, pp.
2-8.
85.
Myers, Norman.
"The Hamburger Connection:
How Central America's
Forests Become North America's
Hamburgers", Ambio, Volume 10, No. 1,
pp. 3-8.
86.
Nations, James D.; and Komer, Daniel I.
"Central America's Tropical
Rainforests: Positive Steps for
Survival", Ambio, Volume 12, No. 5,
1983, pp. 232-238.
87.
Salati, Eneas and Vose, Peter B.
"Depletion of Tropical
Rainforests",
Ambio, Volume 12, No. 2, 1983, pp. 67-71.
88.
Finn, Daniel.
"Land Use and Abuse in the East African Region", Ambio,
Volume 12, No. 6, 1983, pp. 296-301.
89.
Pratt, D.J. and Gwynne, M.D., eds.,
Rangeland Management and Ecology
in East Africa, Huntington, New
York: Robert E. Kreiger Publishing
Company, 1977.
90.
National Academy of Sciences. Environmental
Change in the West African
Sahel, Washington, D.C.:
Board on Science and Technology in
Development,
National Research Council, 1983, 86 pp.
91.
Breman, H. and deWit, C.T. "Rangeland
Productivity and Exploitation in
the Sahel", Science, Volume 221,
1983, pp. 1341-1347.
92.
Kartawinata, Kuswata, Seonartono
Adisoemarto, Soedarsono Riswan, and
Andrew P. Vayda.
"The Impact of Man of a Tropical Forest
in Indonesia",
Ambio, Volume 10, No. 2-3, 1981, pp.
115-119.
93.
Brown, Lester R. "World Population
Growth, Soil Erosion, and Food
Security", Science, Volume 214,
1981, pp. 995-1002.
94.
Grainger, Alain. Desertification, Earthscan,
1984, pp. 94.
95.
O'Keefe, Phil. "The Causes,
Consequences and Remedies of Soil Erosion
in Kenya", Ambio, volume 12, No. 6,
1983, pp. 302-305.
96.
Smith, Nigel J.H. "Colonization Lessons
from a Tropical Forest",
Science, Volume 214, 1981, pp. 755-761.
97.
Gentry, A.H. and J. Lopez-Parodi.
"Deforestation and Increased
Flooding of the Upper Amazon",
Science, Volume 210, 1980, p.1354.
98.
Spears, John.
"Preserving Watershed Environments", UNASYLVA, Volume
34, No. 137, 1982, pp. 10-14.
99.
The State of India's Environment 1984-84.
The Second Citizen's Report
Center for Science and Environment, 807
Vishal Bhavan, 95 Nehru Place,
New Delhi 110 019.
100.
Shukla, J. and Y. Mintz. "Influence of
Land-Surface Evapotranspiration
on the Earth's Climate", Science,
Volume 215, 1982, pp. 1498-1501.
101.
Dosso, Henri, Jean Louis Guillaumet, and
Malcolm Hadley. "Land Use
Problems in a Tropical Forest",
Ambio, Volume 10, No. 2-3, 1981.
102.
National Academy of Sciences. Agro Forestry
in the West African Sahel.
Board on Science and Technology in
Development, National Research
Council, Washington, D.C. 20418. 1983.
86 pp.
103.
Novikoff, Georges and Mohamed Skouri.
"Balancing Development and
Conservation in Pre-Saharan
Tunisia", Ambio, Volume 10, No. 2-3, 1981,
pp. 135-141.
104.
Novikoff, G. "Desertification by
Overgrazing", Ambio, Volume 12, No.
2, 1983, pp. 102-105.
105.
Lamprey, H.F. and Hussein Yussuf.
"Pastoralism and Desert Encroachment
in Northern Kenya", Ambio, Volume
10, No. 2-3, 1981, pp. 131-134.
106.
Anderson, D. and R. Fishwick, Fuelwood
Consumption and Deforestation
in African Countries, World Bank Staff
Working Paper No. 704, 1984.
107.
Smith, Kirk R.; Aggarwal, A.L.; and Dave,
R.M. "Air Pollution and
Rural Fuels: A Pilot Village Study in
India", Working Paper WP82-17,
November 1982. East-West Center,
Honolulu, Hawaii
108.
Smith, Kirk R.; Ramakrishna, Jamuna; and
Menon, Premlata. "Air
Pollution from the Combustion of
Traditional Fuels: A Brief Survey,"
Conference on Air Quality Management and
Energy Policies, Baroda and
Bombay, India, February 16-25, 1981, WP
81-5.
109.
Smith, Kirk R.; Aggarwal, A.L.; and Dave,
R.M. "Air Pollution and
Rural Fuels: Implications for Policy and
Research," Honolulu, Hawaii:
Resource Systems Institute, East West
Center, WP-83-2, November 1982.
110.
de Koning H.W., K.R. Smith and J.M. Last,
"Biomass Fuel Combustion and
Health", Bulletin of the World
Health Organization 63 (1), pp. 11-26,
(1985)
111.
Smith, K., Biomass Fuels, Air Pollution, and
Health: A Global Review,
Plenum Publishing Co., New York,
(forthcoming).
112.
Smith Kirk R., "Biomss Fuels, Air
Pollution and Health" included in
Baldwin, Sam, Howard Geller, Gautam Dutt
and N.H. Ravindranath,
"Improved Woodburning Stoves:
Signs of Success", Ambio Vol. 14, No.
4-5, pp. 280-287, 1985.
113.
Ernest, E. "Fuel Consumption Among
Rural Families in Upper Volta, West
Africa." Eighth World Forestry
Conference, Jakarta, Indonesia, 1978.
114.
If the total fuelwood demand (given by the population
of village, P,
times the demand per person, D) is set
equal to the total renewable
fuelwood supply (given by the average
biomass productivity per area
times the area available for woody
biomass production - - and this area
is given crudely by the total land area, [pi][R.sup.2], less that
needed for
crop production equal to population, P,
times agricultural land needs
per person, A).
Thus, <see equation below>
bsex249.gif (108x600)

The average collection distance will be
approximately the fraction of
R that circumscribes half the area of
radius R, or 0.707R. More
detailed correlations can be developed
as desired, including variable
biomass productivities, inefficiencies
in biomass collection, and
other factors.
115.
Prasad, K. Krishna. Woodburning Stoves:
Their Technology, Economics,
and Deployment, Geneva: International
Labor Organization, 1983.
116.
Eckholm, Eric; Foley, Gerald; Barnard,
Geoffrey; and Timberlake,
Lloyd. Fuelypod: The Energy Crisis That
Won't Go Away, Earthscan,
1984, 105. pp.
117.
Aggarwal, G.C. and N.T. Singh,
"Energy and Economic Returns From
Cattle Dung as Manure and
Fuel" Energy, Vol. 9, No. 1,
pp. 87-90,
1984.
118.
Vidyarthi, Varun. "Energy and the Poor
In An Indian Village" World
Development Vol. 12, No. 8, pp. 821-836,
1984.
119.
Strasfogel, Sylvain.
"Au-dela du choix economique, le choix
ecologique:
le gaz butane au Senegal",
Informations No. 3, November-December
1982, pp. 4-7, Association Bois de Feu.
120.
Baldwin, Sam.
"New Directions in Woodstoves Development" VITA News,
VITA, January 1984.
121.
Strasfogel, Sylvain and Gilles
Dechambre. Programme Regional Foyers
Ameliores - - Le Niger, Aix-En-Provence,
France: CILLS/Association Bois
de Feu, July 1984.
122.
World Bank.
World Development Report, 1984, New York: Oxford University
Press, 1984.
123.
Keita, J.D. "Plantations in the
Sahel," UNASYLVA, V.33,
N.134, pp.
25-29.
124.
National Academy of Sciences.
Firewood Crops, Volume 1, 1980, 237 pp.,
Volume 2, 1983, 87 pp.
125.
Noronha, Raymond.
"Why Is It So Difficult to Grow Fuelwood?",
UNASYLVA, Volume 33, No. 131, 1981, pp.
4-12.
126.
World Bank. Forestry, Sector Policy Paper,
February 1978.
127.
Pant, M.M. "Social Forestry in
India", UNASYLVA, Volume 31, No. 125,
1979, pp. 19-24.
128.
Poulsen, Gunnar. "The Non-Wood Products
of African Forests", UNASYLVA.
129.
Salem, B. Ben and Van Nao, Tran.
"Fuelwood Production in Traditional
Farming Systems", UNASYLVA, Volume
33, No. 131, 1981, pp. 13-18.
130.
Digernes, T.H.
Wood for Fuels: Energy Crisis Implying Desertification:
The Case of Bara, the Sudan,
thesis for the Geografisk
Institutt, Bergen, Norway, 1977, 128 pp.
131.
Hyman, Eric L., "Loan Financing of
Smallholder Treefarming in the
Provinces of Ilocos Norte and Ilocos
Sur, The Philippines," Agro-forestry
Systems Vol. 1, 1983. pp. 225-243.
132.
Hyman, Eric L., "Pulpwood Treefarming
in The Philippines from the
Viewpoint of the Smallholder: An Ex Post
Evaluation of the PICOP
Project," Agricultural
Administration. Vol. 14, 1983. pp. 23-49.
133.
Moreira, J.R. and J. Goldemberg,
"Alcohols - - Its Use, Energy and
Economics - - A Brazilian Outlook",
Resource Management and Optimization
Vol. 1 No. 3, pp. 213-279, 1981.
134.
Geller, H.S., "Ethanol Fuel From Sugar
Cane In Brazil", Annual Review
of Energy, Vol. 10, pp. 135-164, 1985.
135.
Rivera, S. , "Honduras, Country
Study", Global Workshop on End-Use
Oriented Energy Strategies, Sao Paulo,
Brazil, June 1984.
136.
Williams, Robert H., A Low Energy Future For
The United States, Center
For Energy and Environmental
Studies, Report No.
186,
Princeton
University, Princeton, New Jersey,
U.S.A. February 1985.
137.
Gupta, R.K., Efficiency of Utilization of
Domestic Fuels, Indian Oil
Corporation, R & D Centre,
Faridabad; International Seminar on Energy,
Administrative Staff College of India,
Hyderabad, January 1979.
138.
Shaikh, Asif M. and G. Edward Karch,
"Will Wood Work? The Future of
Wood Energy In The West African
Sahel", Special Document, 9th World
Forestry Conference, Mexico City, July
1985.
139.
Moundlic, Jean; "Can Fermentation
Alcohol be Substituted For Wood As A
Cooking Fuel?", Workshop on
Fermentation Alcohol For Use As Fuel and
Chemical Feedstock In Developing
Countries, Vienna Austria, 26-30
March, 1979.
U.N. I.D./WG.293/28, 22 February 1979.
140.
Bradley, P.N., N. Chavangi, and A. Van
Gelder, "Development Research
and Energy Planning In Kenya",
AMBIO, V. XIV, N. 4-5, pp.228-236, 1985
141.
Baldwin, S.; "Domestic Energy For
Developing Countries: Options and
Opportunities", forthcoming.
Reference I-1.
142.
Global Power Supply
and Demand
Global
photosynthesis
1X[10.sup.5] GW(*)
Global
forest biomass growth
5X[10.sup.4]
Global
energy consumption
1X[10.sup.4]
Global
vood consumption
lX[10.sup.3]
Global
fuelwood consumption
5x[10.sup.2]
(*) 1 GW
= 1 billion watts of power.
Reference (10)
More recent
estimates of wood fuel consumption range from roughly 7% (6)
to 14% (20)
of global energy consumption. Thus, the
fuelwood consumption
values
presented in the Table above indicate only the magnitude of use.
143.
Forest Growing
Stock
[m.sup.3]/capita
Africa
92
America, North
179
America, Central
50
America, South
428
Asia
17
Europe
27
USSR
310
Reference (7)
144.
Reducing Factors for
Converting Stacked Wood
To Solid Wood
Content
Reducing
Type
Class
Factor
Softwood
large, round, and straight
0.80
medium split billets, smooth and
straight 0.75
medium split billets, crooked
0.70
small, round firewood
0.70
Hardwood
large split billets, smooth and
straight 0.70
large split billets, crooked
0.65
small round firewood, smooth and
straight 0.65
small round firewood, crooked
0.55
Branches/
twigs
small round
firewood, crooked
0.30-0.45
Brushwood
small round
firewood, crooked
0.15-0.20
Reference
(13)
145.
Production of Crop Residues
from Cereal Crops
in Developing
Countries
Crop
Yield
Residue Production
Metric
tons/ha-year Metric tons/ha-year
Range
Average
Range Average
Rice
0.7-5.7
2.5 1.4-11.4
5.0
Wheat
0.6-3.6 1.5
1.1-6.1
2.6
Maize
0.5-3.7 1.7
1.3-9.3
4.3
Sorghum
0.3-3.2 1.0
0.8-8.0 2.5
Barley
0.4-3.1 2.0
0.7-5.4
3.5
Millet
0.5-3.7 0.6
1.0-7.4
1.2
Reference (20)
146.
Manure Production by
Donesticated Animals
Animal
Metric tons/head-year
Cattle, buffalo, camels
1.00
Horses, donkeys
0.75
Pigs
0.3
Sheep, goats
0.15
Reference (20)
147.
Fuel Use in the
Village Sector
Percent of
Total
from W/cap
Country
Village
Biomass Total
Author
Bangladesh
Dhanishwar
100 190
Bangladesh, 1978
Ulipur
100
238 Briscoe,
1979
Bolivia
Altiplano
352
World Bank, 1983
Botswana
Matsheng
523
White, 1979
Burkina Faso
Ranga
285
Ernst, 1978
Cameroon
Ngaoundere
571
Vennetier, 1979
Chad
N'Djamena
1395
Bertrand, 1977
China
Peipan
87 666
Makhijani, 1975
Congo
Brazzaville
428 Gilbert, 1978
Ethiopia
Addis Ababa
333
FRIDA, 1980
India
Pura
96 285
Reddy, 1979
Injambakkam
95
159 Murugapa
..., 1981
Pemmadapalle(*)
97
112 Bowonder,
1985
Khurpatal
233
Singh et. al., 1979
Bhalutia
275
Singh et. al., 1979
Ungra
95
285
Ravindranath, 1980
Iran
Semnan
571
Vojdani, 1978
Kenya
Machakos
476
Mutula, 1979
Lesotho
Malefiloane 98
260
Best, 1979
Mali
Deguela
241
Caude, 1977
Sanzana
349
Caude, 1977
Bamako
713
Bertram, 1977
Mauritania
Nouakchott
713
FRIDA, 1980
Mexico
Arango
33 412
Makhijani, 1975
Nepal
Hill
97
349 Hughart,
1979
Niger
Niamey
400
Pare, 1979
Niamey
136
Boureima, 1982
Nigeria
Batawagara
99 476
Makhijani, 1975
Kano
571
Grut, 1973
Ibadan
381
Ay, 1978
Rwanda
Nyarugenge(**)
81 1617
Gatera, 1978
Senegal
Dakar(**)
698 Tall, 1974
Sierra Leone
Waterloo
571
Cline-Cole, 1979
Sri Lanka
Anuradhapura
168
Bialy, 1979
Sudan
Khartoum(**)
856
FRIDA, 1980
Tanzania
Bundilya
680
Nkonoki, 1984
Togo
Lome
174
Grut, 1971
(*) Domestic cooking only.
(**) Charcoal.
References primarily compiled and more
completely documented by (20).
Additional data from references
(21,22,61,147B,147C)
147B. B.
Bowonder, N. Prakash Rao, B. Dasgupta, S.S.R. Prasad, "Energy Use
In Eight Rural Communities In
India", World Development, V.13, N.12,
pp.1263-1286, 1985.
147C. World
Bank, "Bolivia: Issues and Options In The Energy Sector",
UNDP/WB Energy Sector Assessment
Program, Rpt. 4213-BO, April 1983.
148.
Power Consumption for Selected
Developing Countries, 1981
Total
Fraction
Total
Fraction
Country
GW
from
Country GW
from
Biomass
Biomass
Angola
3.4
72% Belize
0.2
57
Benin
1.3
89 Costa
Rica 1.8
33
Burkina
Faso 2.2
91 Cuba
19.
35
Burundi
0.3
76 Dominican
Cameroon
6.1
40
Republic 3.3
29
Central
African El
Salvador 2.1
53
Republic
0.9 90
Guatemala
5.4 71
Chad
2.4
96 Haiti
1.9 83
Ethiopia
8.2
90
Honduras 2.3
64
Gabon
1.3
31 Mexico
121.
3
Ghana
3.6
63
Nicaragua 1.7
52
Guinea
1.4
72
Panama
2.4 29
Guinea-Bissau
0.2
77 Bolivia
3.6
44
Ivory
Coast 3.4
65
Brazil
153. 44
Kenya
10.8
81
Colombia 33.
41
Liberia
2.0
65
Ecuador 6.8
26
Madagascar
2.4
76
Paraguay 1.8
73
Mali
1.1
84 Peru
12.
12
Mauritania
0.5
42
Uruguay
3.0
20
Mauritius
0.8
65
Mozambique
4.5
80
Afghanistan 3.0
72
Niger
1.1
79
Bangladesh 7.1
45
Nigeria
46.
64 Burma
9.7
78
Rwanda
1.7
95
China(*) 580.
9
Senegal
1.8
42
Kampuchea 1.4
99
Sierra
Leone 2.7
89 India
196.
36
Somalia
0.7
38
Indonesia
77.
56
Sudan
12.
87 Republic
of
Tanzania
12.
93
Korea 72.
29
Togo
0.5
34 Nepal
4.3
96
Uganda
1.7
83
Pakistan
24.
27
Zaire
4.5
58
Philippines 26.
38
Zambia
3.7
45 Sri
Lanka 3.8
60
Zimbabwe
6.4
40
Thailand 27.
44
Reference
(65); (*) Reference (20) estimates the
fraction as 29%.
149.
More precisely, in a test on eleven fast
growing species the volumetric
gravity of
the charcoal, Y, was found to be typically related to
the specific
gravity of the air dry wood, X, by the equation (14)
Y = 0.575X - 0.069
The
volumetric gravity is the weight of a volume of material, including
pores within,
compared to the weight of an equivalent volume of water.
This is to be
contrasted with specific gravity where pores are often not
counted as
part of the volume, only the material itself is.
150.
This analysis has been previously published
in: T. S. Wood and S.
Baldwin, "Fuelwood and Charcoal Use
in Developing Countries," Annual
Review of Energy, V.10 (1985),
pp.407-429.
151.
Barnard, Geoffrey and Lars Kristoferson,
Agricultural Residues As Fuel
In The Third World, Earthscan,
International Institute for Environment
and Development, Energy Information
Program, Technical Report No.4,
London, 1985.
152.
Foley, Gerald, "Wood Fuel and
Conventional Fuel Demands In The
Developing World", AMBIO, V.14,
N.4-5, pp.253-258, 1985.
153.
Baldwin, Sam, Howard Geller, Gautam Dutt,
and N.H. Ravindranath,
"Improved Woodburning Cookstoves:
Signs of Success", AMBIO, V.14, N.4-5,
pp.280-287, 1985.
154.
Energy Issues and Options In Thirty
Developing Countries, UNDP World
Bank Energy Sector Assessment Program,
Report No. 5230, August 1984.
155.
Foley, Gerald and Geoffrey Barnard, Farm and
Community Forestry,
Earthscan, International Institute for
Environment and Development,
Energy Information Program, Technical
Report No.3, London, 1984.
156.
Foley, Gerald, Charcoal Making In Developing
Countries, Earthscan,
International Institute for Environment
and Development, Energy
Information Programs, Technical Report
No.5, London, January 1986
157.
Notes to Table 19.
(a) Reference 48;
(b) Reference 134;
(c) Reference 133. Note that 11.8
[m.sup.3]/ha-yr is a high yield compared to
those frequently observed, but is only a small fraction of what
should
be achievable.
An annual increment of 11.8 [m.sup.3]/ha-yr at a specific
gravity of 0.8 is equivalent to an
energy capture rate of 0.5 W/[m.sup.2]; or
with an average insolation of 250
W/[m.sup.2], an energy conversion rate of
just 0.2%.
The reason, in part for such low yields is the lack of
inputs such as properly applied
fertilizers and irrigation, or simply
poor species choice for the local conditions.
Approximate
yields for the West African Sahel (1981-1983) are given in
the Table
below.
Wood Production and Yield
In the Sahel
Cost to
Yield
Establish(*) $/ha
Rainfall [m.sup.3]
/ha-yr
Commercial
Plantations 630-1000
600 mm
1.5-3.0
800 mm 3.0-5.0
1000 mm
6.0-10.0
Village
Woodlots 150-388
1.5-3.0
Managed
Natural Forest 80-150
0.5-1.5
(*) Note that
recurrent costs are not included here
but will average
perhaps $100/ha-yr for commercial
plantations and less for the other
options.
Reference
(138)
(d) Reference 24
(e) Reference 136
(f) Reference 137
(g) Shukla, K.C. and J.R. Hurley,
Development of An Efficient Low [NO.sub.x]
Domestic Gas Range Cook Top, Gas Research
Institute, Chicago, Illinois,
1983. Note that this advanced gas stove
has efficiencies of 70%
but is not yet commercially available.
See also W.F. Sulilatu and C.E.
Krist-Spit, "The Tamilnadu Metal
Stove" in From Design to Cooking,
Reference III-35.
(h) Reference 139
(i) See Chapter VI, Charcoal Stoves, and
References therein.
(j) See Chapter V, Table V-1.
(k) See (g) and (j), also see Reference
III-18. Note that side by side
tests in (g) showed wood stoves with thermal
efficiencies of 49-54%
and a natural gas burner in the same
stove having an efficiency of
54%. However, control of the natural gas
burner will be somewhat
better than of a wood fire.
(1) Delivered Energy is that which is
absorbed by the pot in order to cook
the food.
CHAPTER III
1.
Geller, Howard S. and Gautam S. Dutt.
"Measuring Cooking Fuel Economy"
in Wood Fuel Surveys, pp. 147-172. See ref
II-19.
2.
See Reference II-80.
3.
Geller, Howard S. "Fuel Efficiency and
Performance of Traditional and
Innovative Cookstoves", in Wood Heat
For Cooking, Eds. K. Krishna
Prasad and P. Verhaart, Bangalore:
Indian Academy of Sciences, pp.
119-139.
Geller, Howard S. "Cooking in the
Ungra Area: Fuel Efficiency, Energy
Losses, and Opportunities for Reducing
Firewood Consumption", Biomass,
V. 2, 1982, pp. 83-101.
4.
Dunn, P.D.; Samootsakorn, P.; and Joyce, N.
"The Performance of Thai
Charcoal Stoves". in Wood Heat for
Cooking (Ibid.), pp. 107-118. See
also Dunn, P.D.; Samootsakorn, P.; and
Joyce, N. "The Traditional Thai
Cooker" in Energy from Bionamass, 2nd
International Conference on
Biomass, Eds. A. Strub, P. Chartier, and
G. Schleser, London: Applied
Science Publishers, pp. 748-752.
5.
Prasad, K. Krishna and Ernst Sangen (Eds.)
Technical Aspects Of
Woodburning Cookstoves, Woodburning Stove
Group, Eindhoven University
of Technology; and Division of Technology
for Society, Apeldoorn, The
Netherlands. September 1983.
6.
Calculated from controlled cooking test data
in Yameogo, Bussmann,
Simonis, and Baldwin, reference II-80.
7.
The heat gain of the pot on an open fire by
radiant transfer can be
directly extimated by examining the
performance of sultipot massive
stoves with excessive drafts. In such
stoves, radiant transfer does
not change but convective heat transfer is
greatly reduced as the
flames and hot gases are pulled out the
rear of the stove with little
or no contact with the first pot. Typical
PHU's for the first pot in
such stoves are 12 percent (Kaya 2 in
Yaneogo, Bussmann, Simonis and
Baldwin, Reference II-80). Alternatively,
the radiant transfer can be
directly estimated using the
Stefan-Boltzmann law and view factor
between the firebed and pot as discussed
in Appendix C. Model
calculations elsewhere (Bussmann, P.J.T.;
Visser, P.; and Prasad, K.
Krishna, "Open Fires: Experiments and
Theory." pp. 155-188 in Wood
Heat for Cooking (Ibid) ref 3) estimate
the radiant heat transfer
alone to account for about 10 PHU
percentage points of the thermal
efficiency of a pot on an open fire.
The value 17% efficiancy for an open fire
is chosen here to correspond
to test results in the field, ref 6. This
value can be higher if well
protected from the wind, or lower if
exposed to the wind.
8.
Saith, et al. References II-107 to II-112.
9.
Eckert, E.R.G, and Drake, Robert M.,
Jr. Analysis of Heat and Mass
Transfer, New York: McGraw-Hill, 1972, 806
pp.
10. Goller,
H.S. and G.S. Dutt, "Measuring Cooking Fuel Economy", in Wood
Fuel Surveys, See Ref. II-19.
11. Geller,
Howard S.; Leteemane, Bai; Powers, Theresa A.M.; and Sentle,
James.
Prototype Metal and Mud Wood-Burning Cookstoves for Botswana,
Burlington, Vermont: Associates in Rural
Development, May 1983.
12. Ashworth,
John H. The Technology Adaptation Process:
Steps Taken to
Transform the BRET Metal Stove Prototypes
into Finished Commercial
Models, Burlington, Vermont:
Associates in Rural Development, June
1984.
13. Brunet,
Eric personal communication.
14. Sanogo,
Cheick; Sidibe, Yaya; Strasfogel, Sylvain; and Baldwin, Sam.
Results, Technical Notes and Proposals for
the LES Improved Stove
Program.
LES/CILSS/Association Bois de Feu/VITA, October 1983.
Available from VITA.
15. Lokras,
S.S., D.S. Sudhakar Babu, Swati Bhogale, K.S. Jagadish, and R.
Kumar. Development of an Improved Three
Pan Cookstove, Bangalore,
India: ASTRA, Indian Institute of Science,
45 pp.
16. Shailaja,
R. and N.H. Ravindranath. Diffusion of
an Efficient Wood
Stove for Cooking in Rural Areas,
Bangalors, India: ASTRA Indian
Institute of Science, 22 pp.
17.
Ravindranath, N.H. and R. Shailaja. A Field Evaluation of a Fuel-Efficient,
Smokeless Woodstove; ASTRA OLE, Bangalore,
India: ASTRA,
Indian Institute of Science, 25 pp.
18. Mukunda,
H.S. and U. Shrinivasa, Single Pan Wood Stoves of High
Efficiency, ASTRA, Indian Institute of
Science Bangalore, India 560
012, July 1985.
19. Mukunda,
H.S., U. Shrinivasa, S. Dasappa, and S.B. Sunil Lumar, Single
Pan Wood Stoves of High Efficiency, Part
II, ASTRA, December, 1985.
20. Yameogo,
Georges; Ouedraogo, Issoufou; and Baldwin, Sam. Lab Tests of
Fired Clay Stoves, the Economics of
Improved Steady and State
Heat Loss from Masive Stoves, CILSS/VITA,
October 1982. Available
from VITA.
21. Prasad,
K. Krishna (Ed.). Some Studies on Open Fires, Shielded Fires,
and Heavy Stoves.
Apeldoorn, The Netherlands:
Woodburning Stove
Group, Department of Applied Physics and
Mechanical Engineering,
Eindhoven University of Technology and
Division of Technology for
Society, TNO, October 1981, 161 pp.
22. Baldwin,
Sam. See Ref. II-120.
23. Shukla,
K. C. and J.R. Hurley, Development of
An Efficient Low [NO.sub.x]
Domestic Gas Range Cook Top, Gas Research
Institute, Chicago, Illinois,
1983.
24.
Christiaens, M. and G. De Lapeleire,
"Observations on Combustion and
Heat Transfer" in Technical Aspects
of Woodburning Cookstoves. See (5)
25. Emmons,
Howard W. and Arvind Atreya. "The Science of Wood Combustion"
in Wood Heat for Cooking, Prasad,
Verhaart, Eds., Indian Academy of
Sciences, 1983, pp. 5-14.
26. Harker,
A.P., A. Sandels, J. Burley. "Calorific Values for Wood and
Bark and a Bibliography for
Fuelwood," London: Tropical Products
Institute, August 1982.
27. Bussmann,
P.J.T., P. Visser and K. Krishna
Prasad. "Open Fires:
Experiments and Theory" in Wood Heat
for Cooking. See Ref. 3.
28. Sangen,
E. "A Survey of Test Results in Wood Stoves" in Technical
Aspects of Woodburning Cookstoves,
Eindhoven, 1983. See ref 5.
29. Personal
communication with Kirk Smith, 1984.
30. To calculate
the calorific value of the wet biomass for the different
moisture content definitions, tables as
sketched below can be developed
where the energy to evaporate water from
25[degrees]C is 2575 kJ/kg.
Wood
Moisture Content
Measured on a
Dry
Basis Wet Basis
Moisture Content
30%
30%
Equivalent Dry Wood per kg of Biomass
1.0 kg
0.7 kg
Water Content per kg of Biomass
0.3 kg
0.3 kg
Total, equivalent dry wood plus water
1.3 kg
1.0 kg
Gross Energy per kg of Biomass
18 MJ
12.6 MJ
Less Energy To Evaporate Water
per kg Dry Biomass
17.227 kJ
11.827 kJ
Net Energy per kg Wet Biomass
13.252 MJ
11.827 MJ
31. Shelton,
Jay. The Woodburners Encyclopedia,
Waitsfield, Vermont:
Vermont Crossroads Press, Ninth printing,
1979, 126 pp.
32. Stevens,
W.C. and G.H. Pratt, Kiln Operators Handbook, Department of
Scientific and Industrial Research, Her
Majesty's Stationery Office,
London, 1952, 138 pp.
33. Prasad,
K. Krishna; Sangen, E.; Visser, P. "Woodburning Cookstoves",
In Advances Tn Heat Transfer, Eds., James
P. Hartnett and Thomas F.
Irvine, Jr. Volume 17, pp. 159-317,
Academic Press, N.Y. 1985.
34.
Ouedraogo, Issoufou; Yameogo, Georges; and Baldwin, Sam. Lab Tests of
Fired Clay and Metal One-Pot Chimneyless
Stoves, IVE/CIIAS/VITA,
February 1983. Available from VITA.
35.
Krist-Spit, C.E., "The Combustion Quality of the Charcoal Stoves
Sakkanal and Malgache" in From Design
To Cooking, eds. C.E. Krist-Spit
and D.J. vander Headen, Woodburning Stove
Group Eindhoven University
of Technology; and Division of Technology
of Society, Apeldoorn, The
Netherlands. January, 1985.
36. Wood,
Timothy S., "Laboratory and Field Testing of Improved Stoves In
Upper Volta", National Academy of
Sciences, BOSTID, Washington, DC,
1981, pp.23
37. De
Lepeleire, G. and M. Christiaens. "Heat Transfer and Cooking
Woodstove Modelling" in Wood Heat for
Cooking. Ref. (3).
38. Waclaw
Micuta, "Modern Stoves For All", Intermediate Technology
Publications, London, and the Bellerive
Foundation, 1985.
The alternative of extinguishing the fire
and placing a highly
insulating jacket over the stove and pot
together is a second possibility.
In this case, the remaining coals would
help maintain the
temperature. However, even with a tightly
fitting lid, there may be a
problem due to excessive smoke and carbon
monoxide entering the pot
and contaminating the food. This needs to
be tested.
39. The
calculation was done using the conductive heat loss program for
double walls (Appendix A), setting the
initial temperature distribution
of the massive outer wall to that for a
single wall stove
running for 60 minutes, and setting the
parameters and temperatures of
the inner wall to that for cold water.
40. Zhu,
Brambley, and Morgan, Reference II-57.
41. Foley,
Gerald, and Geoffrey Barnard, Biomass Gasification In Developing
Countries, Earthscan, International
Institute For Environment
and Development, Energy Information
Programme, Technical Report No.1,
London, 1983.
42. As a more
quantitative example of the importance of control, a simple
illustrative calculation of energy use by
two hypothetical stoves and
pots is given below. Capabilities of these
stoves and pots are given
in Table A. Given these parameters, the
time to reach a boil is given
by <see equation below>
bsex260.gif (393x600)

For pot loss
rates of about 700 W/[m.sup.2] (Reference 43) and an exposed pot
area of about
0.14 [m.sup.2], total pot losses are then 100 W/[m.sup.2]. This gives
t = 8x[10.sup.5]/(800-100) = 1140 seconds
The total
amount of energy used to bring the pot to a boil is then
E = (1140 s)x(2000 W) = 2.28 MJ
The power
level for simmering is determined by the minimum level
necessary to
make up for the heat losses from the pot.
Lids are
assumed to be
used, so steam losses are not included.
Such steam
TABLE A
Hypothetical Stove and Pot
Performance
Stove A Stove B
High Power
2 kW
4 kW
Thermal Efficiency
40%
40%
Low Power
0.5 kW
0.2 kW
Thermal Efficiency
40%
30%
Pot 1
Pot 2
Heat Loss
100 W 25 W
TABLE B
A Hypothetical
Cooking Task
Stove/Pot
A/1
A/2 B/1
B/2
Time to Boil (minutes)
19
17 9
8
Energy Used (MJ)
2.29
2.06
2.13 2.03
Simmering Power (kW)
0.5
0.5 0.3
0.2
Excess Energy to Steam(*)(kW)
0.1
0.175 0.0
0.035
Energy Used to Simmer (MJ)
1.8
1.8 1.08
0.72
Total Energy Used (MJ)
4.09
3.86 3.21
2.75
Actual Energy Needed(**)(MJ)
1.16
0.89 1.16
0.89
Overall Cooking Efficiency
28%
23% 36%
32%
(*) This is the difference between
the energy input to the pot at the
firepower closest to the minimum
needed and the heat losses from the
pot. Thus (0.5 kW)(0.4 efficiency) -
(100 W pot loss) = (100 W to steam)
(**) The actual energy needed for the
cooking task is the energy
required to bring the 10 kgs. of food
to a boil and maintain that
temperature for one hour.
losses are
due to excessive fire powers. The
amount of energy then
used during
one hour of simmering is the fire power times 3600
seconds.
Total energy
consumption for bringing the food to a boil and then
simmering it
for one hour can then be calculated and the result
compared to
the ideal case as done in Table B.
Several
features in Table B stand out. First, although Stove A had a
higher
efficiency than Stove B during the simmering phase, its overall
cooking
efficiency was lower because its firepower could not be
reduced below
0.5 kW. Second, insulation on the pot strongly
influenced
the amount of
energy used. Third, the overall cooking
efficiency
was not a
good indicator of total energy consumption by the
stove.
Fourth, the ability to reach high power
levels saved time,
typically
about 10 minutes, and also saved energy due to a shorter
period that
the pot could lose heat to the environment.
43. G. De
Lepeleire and M. Christaens, "Heat Transfer and Cooking Woodstove
Modelling", in Wood Heat For Cooking,
eds. K. Krishna Prasad and
P. Verhaart, Indian Academy of Sciences,
Bangalore 560 080, 1983.
CHAPTER IV
1.
Yameogo, Bussmann, Simonis, Baldwin, Ref.
II-80.
2.
Improved Biomass Cooking Stove For Household
Use, Forest Products
Research Division, Royal Forest
Department, Ministry of Agriculture
and Cooperation; and National Energy
Administration, Ministry of
Science, Technology, and Energy, Royal
Thai Government; and USAID,
1984.
3.
Selker, John S., Laurie F. Childers, and
Peter J. Young. Development
of Stoves For Use In Urban Areas of Sri
Lanka: Interim Technical
Report, ITDG, London, November, 1985
CHAPTER V
1.
Testing the Efficiency of Woodburning
Cookstoves: Provisional International Standards.
Arlington, Virginia: VITA, December 1982,
76 pp.
2.
Testing the Efficiency of Woodburning
Cooktoves: Provisional International
Standards. Arlington, Virginia: VITA,
Revised, May 1985.
There are several important changes in
these updated procedures
compared to reference (1). First, the 15
minute extension of the high
power phase vas eliminated because it did
not improve the resolution
of the test, only its duration. Second,
lids are not used. Lids proved
to be cumbersome in practice and
additionally did not reduce the
scatter in the data but rather increased
it.
Additionally, in this book the index for
evaluating the stoves'
performance in the lab is changed from
(wood used)/water evaporated to
PHU or SC because these are better
indicators of a stove's performance
and because these indices better
correspond to those for controlled
cooking or field tests.
It is important to note the interaction
between the use of a lid on
the pot and the index used to evaluate the
stove's performance. If a
lid is used then the amount of water
evaporated and escaping is
somewhat dependent on the tightness of the
lid's fit to the pot, and
extremely dependent on the firepower.
If the firepower is low so that
the temperature is maintained a few
degrees below boiling, effectively
no water vapor will escape.
If the firepower is high enough so that
the water boils, the escaping steam will
push the lid open and escape.
(The partial pressure of the water vapor
is greater than atmospheric
pressure.) In this case there will be a
large amount of water evaporated
from the pot.
The index, wood/water evaporated, is then very
sensitive to how well the firepower is
controlled. The PHU is
similarly sensitive due to the measure of
the heat absorbed by the pot
being given in part by the water
evaporated. Heat is still absorbed,
but is not measured as the water vapor
condenses on the lid and falls
back in.
The heat is instead lost by convection from the pot lid.
Finally, for specific consumption defined
as wood/(initial water), the
amount of evaporation has no effect.
For specific consumption defined
as (wood used)/(final water) or (wood
used)/(water "cooked"), evaporation
has an effect but a less significant one.
When no lid is used, then the index (wood
used)/(water evaporated) is
still sensitive to the firepower while PHU
and SC are relatively
insensitive to it.
By not using a lid, evaporation rates are
higher and the stove must be
run at a somewhat higher power to maintain
the temperature than is the
case with a lid.
Thus, when not using a lid the low power performance
of the stove is not really being evaluated
during the second phase.
In this context, it is important to note
the difference in control
between wood stoves and charcoal stoves.
Tests conducted by the author in
collaboration with IBE, Burkina Faso
unpublished) showed a large variation
between tests in firepower and
evaporation rates when operating the stove
at a very low power level
(with lids).
The reason for this was that without a consistent size
of wood and precise fire feeding
timetable, maintaining a very low
power proved to be more a function of the
tester's patience and
conscientiousness and of the wood size and
moisture content than of
the stove design.
In daily use in the field, users certainly
do not
control woodstoves to this degree to
optimize their low power phase
fuel consumption.
In contrast, the low power capability of a
charcoal stove is a
function of the air tightness of its door
and additionally is determined
by the formation of the ash layer on the
surface of the burning
charcoal, slowing its combustion (Appendix
D). Very low power tests
of
charcoal stoves (by using a lid on the pot), then, do directly test
the stove itself (its airtightness) and
thus &re recommended (Chapter
VI).
3. The specific consumption is defined as
(wood used)/(water remaining at
end of test) rather than (wood
used)/(water at start of test) because
this index corresponds to the form used
for the controlled cooking
tests and to the concept of (wood
used)/(water "cooked").
Although
this index is sensitive to excess
evaporation (see ref. 2) it is still
sufficiently robust to be a useful
indicator.
In cases where there is a large daily or
seasonal variation in ambient
temperature it may be desirable to
normalize the specific consumption
according to the initial water temperature.
4. Particularly useful is using a factorial
design for the experiment and
then performing an analysis of variance
and a multiple regression on
the data.
This however is beyond the scope of the section on statistics
and the reader is referred to a basic text
on the subject such as
Reference (16) below.
5. Yameogo, Bussmann, Simonis, and
Baldwin. Reference II-80.
6. Strasfogel, Deschambre.
Reference II-121.
7. Yameogo, Ouedraogo, Baldwin.
Reference III-20.
8. Ouedraogo, Yameogo, Baldwin.
Reference III-34.
9. Sanogo, Sidibe, Strasfogel, Baldwin.
Reference III-14.
10. Dutt,
Gautam, M. Hassan. "Efficient
Cookstove Development in Somalia:
A Progress Report".
Arlington, VA:
VITA, July 1984.
11. Sepp,
Cornelia. "Production and
Dissemination of Improved Stoves -- A
Case Study", Ouagadougou, Burkina
Faso: German Forestry Mission,
September 1983, pp.17
12. Sepp,
C. "Un Foyer Metallique a un trou
pour la Haute-Volta", Informations,
Marseille, France:
Association Bois de Feu, No. 5,
April-May-June
1983, pp. 20-21.
13. Baldwin,
reference II-120.
14.
UNFAO. Wood Fuel Surveys. ref II-19.
15. National
Academy of Sciences. Proceedings of the
International
Workshop on Energy Survey Methodologies
for Developing Countries.
BOSTID, National Academy Press, 1980.
16. Hyman,
E.L., "How to Conduct A Rural Energy Survey In a Developing
Country", Renewable Sources of
Energy, Vol. VI, No.2, pp. 137-149
(1983)
17.
Smale, Melinda;
Savoie,
Michelle; Shirwa, Zahra Cabdi;
and Axmed,
Mohamed Cali.
Wood Fuels Consumption and Cooking Practices in Selected
Sites of Lower Shabeelle, Banaadir, and
Gedo Regions of Somalia.
Arlington, Virginia:
VITA, July 1984, 151 pp.
18. Ki Zerbo,
J. Improved Wood Stoves:
Users' Needs and Expectations in
Upper Volta.
Arlington, Virginia:
VITA, 1980.
19. Wood,
Timothy, "Laboratory and Field Testing of Improved Stoves In
Upper Volta" National Academy of
Sciences (BOSTID), Washington, D.C.,
1981.
20. Dutt,
Gautam; Field Evaluation of Woodstoves, VITA, Arlington,
Virginia:
1981.
21. Hyman,
Eric L., "Analysis of The Wood Fuels Market:
A Survey of
Fuelwood Sellers and Charcoal Makers in
The Province of Ilocos Norte,
Philippines", Biomass V.3, 167-197.
(1983).
22. Cited in
Michael R. Brambley and Thomas Medynski, Evaluation of
Biomass Briquettes As Cookstove Fuel:
An Experimental Study, Department
of Engineering and Policy, Center for
Development Technology,
Washington University, St. Louis,
Missouri, July 1984.
ASTM Standard D2395-69, Standard Method of
Test For Specific Gravity
of Wood and Wood Base Materials, American
Society For Testing and
Materials, Philadelphia, Pennsylvania,
1977.
ASTM Standard D2016-74, Standard Method of
Test For Moisture Content
of Wood, 1974.
ASTM Standard D1102-56, Standard Method of
Test For Ash In Wood, 1978.
ASTM Standard D2015, Standard Method of
Test For Gross Calorific Value
of Solid Fuel By The Adiabatic Bomb
Calorimeter, 1972.
ASTM Standard D3175-77, Standard Test For
Volatile Matter In The
Analysis Sample of Coal and Coke, 1977.
ASTM Standard D3172-73, Standard Method
for Proximate Analysis of Coal
and Coke, 1979.
23. Although
the natural scale for water to be normalized to is 100[degrees]C, it
is convenient to divide instead by
75[degrees]C (i.e. normalize it to 25[degrees]C) so
that the results don't differ too
significantly from the unnormalized
values.
24.
Examples of total village energy use studies
include: Nkonoki and
Sorensen, reference II-21; Singh, Pandey
and Tiwari, reference II-22;
Ravindranath, et. al., reference II-50;
Reddy, reference II-51; Down,
reference II-58; Bowonder, et. al.,
reference II-147. In particular,
the interested reader should review
Ravindranath et. al. and Reddy.
25. Agarwal,
Bina, "Diffusion of Rural Innovations:
Some Analytical Issues
and the Case of Wood-Burning Stoves",
World Development, V.11, N.4,
pp.359-376, 1983.
CHAPTER VI
1. Kinyanjui, M.
"The Kenya Cookstove Project, 1981-1983", UNFAO,
October
1983, 37 pp.
2. M. Kinyanjui, "The Kenya Charcoal
Stoves Program: Interim Report",
Energy/Development International, USAID,
Washington, D.C. June 1984.
3. Eric L. Hyman, "The Economics of
Fuel-Efficient Household Charcoal
Stoves In Kenya", Appropriate
Technology International, Washington,
D.C. 1985, to be published.
Eric L. Hyman, "The Strategy of
Decentralized Production and Distribution
of Improved Charcoal Stoves In
Kenya", Appropriate Technology
International Washington, D.C., 1985, To
be published.
Eric L. Hyman, "The Experience With
Improved Charcoal and Wood Stoves
for Households and Institutions In
Kenya", ATI, Washington, D.C.,
December 1985.
4. Simon Burne, "Charcoal Stove
Developments In Kenya: The Present and
The Future", ITDG, Rugby, U.K., Aug.
1985.
5. Joseph, Stephen; "Advisory Visit To
The Stoves Project of MOERD/KENGO,
Kenya", Intermediate Technology
Development Group, London, England,
September, 1984.
6. Ministry of Science, Technology, and
Energy, Royal Thai Government,
Reference IV-2.
7. Dunn, Samootsakorn, Joyce; Reference III-4.
8. Sherman, Marcus, William Steward, and
Banyat Srisom, "An Evaluation of
Thai Cooking Fuels and Stoves",
Renewable Energy Review Journal V.5,
N.1 pp.60-65, April 1983.
9. Baldwin, reference II-79.
10. See
reference and note V-2.
11. C.E.
Krist-Spit, reference III-35.
12. Dutt,
Gautam. "Efficient Cookstove
Development in Somalia: A Progress
Report." VITA, 1984.
13. See ref
V-3.
14. Yameogo,
Bussmann, Simonis, Baldwin, reference II-80.
15. Sanogo,
Sidibe, Strasfogel, Baldwin, reference III-14.
16. Koenig,
Delores. Laboratoire Energie Solaire,
Bamako, Mali, 1983
unpublished.
17. National
Academy of Sciences, Reference II-124.
APPENDIX A
1. Eckert, E.R.G., and Drake, Robert M.,
Jr. Analysis of Heat and Mass
Transfer.
New York: McGraw-Hill, 1972.
2. For a discussion of the specific heat at
constant pressure [c.sub.p], the
specific heat at constant volume
[c.sub.v], and their respective uses, see
reference (1) above, F. Reif, Fundamentals
of Statistical and Thermal
Physics, McGraw-Hill, New York 1965, or
other basic thermodynamics
texts.
3. Duffie, John A., Beckman, William A.
Solar Energy Thermal Processes.
New York:
John Wiley and Sons, 1974.
4. Ozisik, M. Necati.
Heat Conduction.
New York: John Wiley and
Sons,
1980.
5. Holman, J.P. Heat Transfer.
New York:
McGraw-Hill, 1981.
[k.sub.e] is derived from the empirical
equation <see equation below>
bsex267.gif (135x540)

where C=0.197, n=0.25, and m=0.111; and
the temperatures are fit to
exponentials as discussed in Appendix C.
6. These and other numerical data are
available from the author by
request.
APPENDIX B
1. Arpaci, Vedat S. , and Larsen, Paul
S. Convection Heat Transfer.
Englewood Cliffs, New Jersey:
Prentice-Hall, Inc., 1984.
2. Burmeister, Louis C.
Convective Heat Transfer.
New York:
John Wiley
and Sons, 1983.
3. Cebeci, Tuncer, and Bradshaw, Peter.
Physical and Computational
Aspects of Convective Heat Transfer, New
York, Springer-Verlag, 1984.
4. Eckert, ref A-1.
5. Jaluria, Y.
Natural Convection: Heat
and Mass Transfer, Volume 5 of
The Science and Applications of Heat and
Mass Transfer. Oxford:
Pergamon Press, 1980.
6. Gray, Donald R., and Giorgini, Aldo.
"The Validity of the Boussinesq
Approximation for Liquids and Gases",
Int. J. Heat and Mass Transfer,
Volume 19, 1976, pp. 545-551.
7. Holman, J.P.
Heat Transfer. New
York: McGraw-Hill, 1981.
8. Kanury, A. Murty.
Introduction to Combustion Phenomena.
New York:
Gordon and Breach, 1975.
9. Rohsenow, Warren M., and Hartnett, James
P., Eds. Handbook of Heat
Transfer.
New York: McGraw-Hill, 1973.
10. Shah,
R.K., and London, A.L. "Laminar
Flow Forced Convection in Ducts"
in
Advances in Heat Transfer, J.P.
Hartnett and T.F. Irvine, Eds.,
Supplement 1.
New York: Academic Press,
1978.
11. Bussmann,
P.J.T.; Visser,
P.;
and Prasad, K. Krishna.
"Open Fires:
Experiments and Theory," in Wood Heat
for Cooking, K. Krishna Prasad
and P. Verhaart, Eds.,
Bangalore:
Indian Academy of Sciences, 1983,
pp. 155-188.
See also Prasad, Sangen, and Visser, Reference III-33.
12. Conolly,
R., and Davies, R.M. "A Study of
Convective Heat Transfer
from Flames", in The International
Journal of Heat and Mass Transfer,
Volume 15, 1972, pp. 2155- 2172.
13. Cox, G.,
and Chitty, R. "A Study of the
Deterministic Properties of
Unbounded Fire Plumes", in Combustion
and Flame, Volume 39, 1980, pp.
191-209.
14. Cairnie,
L.R. and A.J. Harrison. "Natural
Convection Adjacent to a
Vertical Isothermal Hot Plate with a High
Surface-to-Ambient Temperature
Difference", in The International
Journal of Heat and Mass
Transfer, 1982, pp. 925-934.
15. Petukhov,
B.S. and A.F. Polyakov. "Buoyancy
Effect on Heat Transfer in
Forced Channel Flows", Seventh
International Heat Transfer Conference
Proceedings, Volume 1, pp. 343-362,
Washington: Hemisphere Publishing
Corporation, 1982.
16. Lee, Shao-Lin
and H.W. Emmons. "A Study of
Natural Convection Above a
Line Fire", in The Journal of Fluid
Mechanics, Volume VII, 1961, pp.
353-368.
17. Yameogo,
Ouedraogo, Baldwin, ref III-20; Ouedraogo, Yameogo, Baldwin,
ref III-34.
18. Sangen,
E. "A Survey of Test Results in
Wood Stoves" in Technical
Aspects of Woodburning Stoves, Prasad and
Sangen, Eds. Eindhoven,
1983.
19.
Horsley, M.E.;
Purvis, M.R.I.; and Tariq, A.S.
"Convective Heat
Transfer from Laminar and Turbulent Premixed
Flames", Seventh International
Heat Transfer Conference, Volume 3, pp.
409-415, Washington,
D.C.:
Hemisphere Publishing Company, 1982.
20. Faster,
more precise algorithms for finding the roots [T.sub.i] than used
here are widely available.
See, for example, S.D. Conte and Carl de
Boor, Elementary Numerical Analysis, 2nd
Edition, McGraw-Hill, 1972,
or Eugene Isaacson and Herbert Bishop
Keller, Analysis of Numerical
Methods, John Wiley and Sons, 1966.
Such techniques are not generally
necessary for the simple case here.
21.
Delepeleire, G., and Christiaens, M.
"Heat Transfer and Cooking
Woodstove Modelling", in Wood Heat
for Cooking, K. Krishna Prasad and
P. Verhaart, Eds., Bangalore:
Indian Academy of Sciences, pp. 189-200.
22. Hughes,
T.J.R., Ed. Finite Element Methods for
Convection Dominated
Flows.
New York: American Society of
Mechanical Engineers, 1979.
23. Roache,
Patrick J. Computational Fluid
Dynamics. Albuquerque, New
Mexico:
Hermosa Publishers, 1976.
24. Shih,
T.M. Numerical Heat Transfer.
Washington, D. C.:
Hemisphere
Publishing Corporation, 1982.
25. Shih,
T.M. , Ed. Numerical Properties and
Methodologies in Heat
Transfer.
Washington, D.C.: Hemisphere
Publishing Corporation, 1983.
26. Bodoia,
J.R. and J.F. Osterle. "The
Development of Free Convection
Between Heated Vertical Plates", in
The Journal of Heat Transfer,
Transactions ASME, February 1962, pp.
40-43.
27. Aung,
W., L.S.
Fletcher, and V.
Sernas.
"Developing Laminar Free
Convection Between Vertical Flat Plates
with Assymmetric Heating", in
The International Journal of Heat and Mass
Transfer, Volume 15, 1972,
pp. 2293- 2308.
Aung, W.
"Fully Developed Laminar Free Convection Between Vertical
Plates Heated Assymmetrically", in
The International Journal of Heat
and Mass Transfer, Volume 15, 1972, pp.
1577-1580.
28. Back,
Lloyd H. "Very High Temperature
Laminar Flow of a Gas Through
the Entrance Region of a Cooled Tube --
Numerical Calculations and
Experimental Results", in The
International Journal of Heat and Mass
Transfer, Volume 15, 1972, pp. 1001-1021.
29. Bradley,
D. and A.G. Entwistle. "Developed
Laminar Flow Heat Transfer
from Air for Variable Physical
Properties", in The International
Journal of Heat and Mass Transfer, Volume
8, 1965, pp. 621-638.
30. Leonard,
B.P. "A Stable and Accurate
Convective Modeling Procedure
Based on Quadratic Upstream
Interpolation," in Computer Methods in
Applied Mechanics and Engineering, Volume 19, 1979, pp. 59-98.
31.
Cebeci, T.;
Khattals, A.A.;
and Lamont, R.
"Combined Natural and
Forced Convection in Vertical Ducts."
Seventh International Heat
Transfer Conference, Volume 3, pp. 419-424,
Washington, D.C.: Hemisphere
Publishing Co., 1982.
32. Dalbert,
A.M. "Natural, Mixed and Forced
Convection in a Vertical
Channel with Assymmetric Uniform
Heating." Seventh International Heat
Transfer Conference, Volume 3, pp.
431-434, Washington, D.C.: Hemisphere
Publishing Co., 1982.
33.
Kettleborough, C.F. "Transient
Free Convection Between Heated Vertical
Plates Including Entrance Effects",
Int, J. Heat Mass Transfer, Vol.
15, pp. 883-896, 1972.
APPENDIX C
1. Eckert and Drake, ref A-1.
2. Ozisik, M. Necati.
Radiative Transfer and Interactions with
Conduction
and Convection.
New York: John Wiley and
Sons, 1973.
3. Siegel, Robert, and Howell, John R.
Thermal Radiation Heat Transfer.
2nd Edition.
New York: McGraw Hill,
1981.
4. See F.R. Steward and R. Gaulard in
Blackshear, Perry L., Ed. Heat
Transfer in Fires:
Thermophysics, Social Aspects, Economic
Impacts.
New York:
John Wiley and Sons, 1974.
5. Prasad, Sangen, Visser, ref III-33.
6. Lowes, T.M., and Newall, A.J.
"The Emissivities of Flame Soot
Dispersions",
in Combustion and Flame, Volume 16, 1971,
pp. 191-194.
7. Felske, J.D., and Tien, C.L.
"Calculation of the Emissivity of
Luminous Flames", in Combustion Science
and Technology, Volume 7,
1973, pp. 25-31.
8. Sibulkin, Merwin.
"Estimates of the Effect of Flame Size
on Radiation
from Fires", in Combustion Science
and Technology, Volume 7, 1973, pp.
141-143.
9. King, N.K.
"The Influence of Water Vapor on the Emission Spectra of
Flames", Combustion Sci. and Tech.,
Volume 6, 1973, pp. 247-256.
10. Tien,
C.L. and S.C. Lee. "Flame Radiation", in Prog. Energy Combustion
Science, Volume 8, 1982, pp. 41-59.
11. Modak,
Ashok T. "Thermal Radiation from
Pool Fires", in Combustion and
Flame, Volume 29, 1977, pp. 177-192.
12. Modak,
Ashok T. "Nonluminous Radiation
from Hydrocarbon-Air Diffusion
Flames", in Combustion Sci, and
Tech., Volume 10, 1975, pp. 245-259.
13. Kurosaki,
Yasuo; Mishima, Hiroshi; and Kashiwagi, Takao.
"Heat
Transfer Combined with Radiation and
Natural Convection in a Rectangular
Enclosure", in Seventh International
Heat Transfer Conference
Proceedings, Volume 2, pp. 215-220, New
York: Hemisphere Publishing
Corporation and McGraw-Hill International,
1982.
APPENDIX D
1. Graboski, M., and Bain, K.
"Properties of Biomass Relevant to
Gasification"
in Biomass Gasification.
Principles and Technology.
T.B.
Reed, Ed.
Park Ridge, NJ: Noyes Data
Corporation.
2. Stubington, J.F., and Fenton, H.
"Combustion Characteristics of Dried
and Pelletized Bagasse" in Combustion
Science and Technology, Volume
37, 1984, pp. 285-299.
3. See also C.A. Zaror and D.L.
Pyle, "The Pyrolysis of Biomass:
A
General Review" in Wood Heat for
Cooking, reference III-3.
4. Harker, A.P.; Sandels, A.; and Burley,
J. Calorific Values for Wood
and Bark and a Bibliography for Fuelwood.
56/62 Gray's Inn Road, WC1X
8LU, London, England:
Tropical Products Institute, August 1982.
5. Kjellstrom, B.
Producer Gas.
Stockholm: Beijer Institute,
1980.
6. National Academy of Sciences.
Firewood Crops:
Shrub and Tree Species
for Energy Production.
Volume 1, 1980, Volume II, 1983, Washington,
D.C.:
National Academy Press.
7. Abe, Fusako.
"Manufacture of Charcoal from Fast-Grown Trees" in
Energy
from Forest Biomass, W. Ramsey Smith, Ed.
New York: Academic Press,
1982, pp. 129-146.
8. Kanury, A. Hurty, and Blackshur, Perry
L., Jr.
"Some Considerations
Pertaining to the Problem of Wood
Burning" in Combustion Science and
Technology, Volume VI, 1970, pp. 339-355.
9. Roberts, A.F.
"A Review of Kinetics Data for the Pyrolysis of Wood and
Related Substances" Combustion and
Flame, Volume 14, 1970, pp. 261-272
10. Bhagat,
Phiroz M. "Wood Charcoal
Combustion and the Effects of Water
Application" in Combustion and Flame,
Volume 37, 1980, pp. 275-291.
11. Bhagat,
Phiroz M. "Analytical Modeling of
the Effects of Water
Application on Burning Wood Charcoal
Surfaces" in Combustion and
Flame, Volume 47, 1982, pp. 93-98.
12. Atreya,
Arvind. "Fire Growth on Horizontal
Surfaces of Wood" in
Combustion Science and Technology, Volume
39, 1984, pp. 163-194.
13. Kanury,
A. Murty. Introduction to Combustion
Phonomena. New York:
Gordon and Breach, 1982.
14. Glassman,
Irvin. Combustion.
New York:
Academic Press, 1977.
15.
Buckmaster, J.D., and Ludford,
G.S.S.
Theory of Laminar Flames.
Cambridge University Press, 1982.
16. Toong,
Tau-Yi. Combustion Dynamics. New York:
McGraw-Hill, 1983.
17. Bamford,
C.H.; Crank, J.; and Malan, D.H.
"The Combustion of Wood,
Part I" in Proceedings of the
Cambridge Philosophical Society, Volume
42, Part 2, 1946, pp. 166-182.
18.
Blackshear, Perry L., and Kanury, A. Murty.
"On the Combustion of Wood
I:
A Scale Effect in the Pyrolysis of Solids" in Combustion Science
and Technology, Volume 2, 1970, pp. 1-4.
19. Kanury,
A. Murty, and Blackshear, Perry L., Jr.
"On the Combustion of
Wood II:
The Influence of Internal Convection on the Transient
Pyrolysis of Cellulose" in Combustion
Science and Technology, Volume
2, 1970, pp. 5-9.
20. Kanury,
A. Murty.
"Thermal Decomposition Kinetics of Wood Pyrolysis"
in Combustion and Flame, Volume 18, 1972,
pp. 78-83.
21. Kanury,
A. Murty. "Rate of Burning of
Wood" in Combustion Science and
Technology, Volume 5, 1972, pp. 135- 146.
22. Kung,
Hsiang-Cheng. "A Mathematical
Model of Wood Pyrolysis" in
Combustion and Flame, Volume 18, 1972, pp.
185-195.
23. Kung,
Hsiang-Cheng and Ashok S. Kalelkar.
"On the Heat of Reaction in
Wood Pyrolysis" in Combustion and
Flame, Volume 20, 1973, pp. 91-103.
24. Havens, J.A.;
Hashemi, H.T.; Brown, L.E.; and Welker, J.R.
"A Mathematical
Model of the Thermal Decomposition of
Wood" in Combustion
Science and Technology, Volume 5, 1972,
pp. 91-98.
25. Maa,
Peter S., and Bailie, Richard C. "Influence of Particle Sizes
and Environmental Conditions on High
Temperature Pyrolysis of Cellulosic
Material-I (Theoretical)" in
Combustion Science and Technology,
Volume 7, 1973, pp. 257-269.
26. Kansa,
Edward J.; Perlee, Henry E.; and Chaikin, Robert F.
"Mathematical
Model of Wood Pyrolysis Including Internal
Forced Convection"
in Combustion and Flame, Volume 29, 1977,
pp. 311-324.
27. Roberts,
A.F. "The Heat of Reaction During
the Pyrolysis of Wood in
Combustion and Flame, Volume 17, 1971, pp.
79-86.
28. Broido,
A.; and Nelson, Maxine A. "Char
Yield on Pyrolysis of Cellulose"
in Combustion and Flame.
Volume 24, 1975, pp. 263-268.
29. Milne,
T. "Pyrolysis -- The Thermal
Behavior of Biomass Below 600 [degrees]C"
in Biomass Gasification.
Principles and Technology,
T.B. Reed, Ed.
Park Ridge, New Jersey:
Noyes Data Corporation, 1981, 401 pp.
30.
Desrosiers, R. "Thermodynamics of
Gas-Char Reactions" in T.B. Reed,
ref 29.
31. Graboski,
M. "Kinetics of Char Gasification
Reactions." in T.B. Reed,
ref 29.
32. Williams,
F. "Condensed-Phase Mass and
Energy Balances" in Heat
Transfer in Fires:
Thermophysics, Social Aspects, Economic
Impacts,
Perry L. Blackshear, Ed.
New York:
John Wiley & Sons, 1974.
33. Williams,
F.
"Chemical Kinetics of Pyrolysis" in Heat Transfer in
Fires.
34.
Roberts, O.C.,
and Smith, I.W.
"Measured and Calculated Burning
Histories of Large Carbon Spheres in
Oxygen" in Combustion and Flame,
Volume 21, 1973, pp. 123-127.
35. Adomeit,
G.; Mohiuddin, G.; and Peters, N.
"Boundary Layer Combustion
of Carbon" in Sixteenth International
Symposium on Combustion,
Combustion Institute, 1976.
36.
Ubhayakar, Shivadev K. "Burning
Characteristics of a Spherical
Particle Reacting with Ambient Oxidizing
Gas at Its Surface" in
Combustion and Flame, Volume 26, 1976, pp.
23-24.
37. Beshty,
Bahjat S. "A Mathematical Model
for the Combustion of A Porous
Carbon Particle", in Combustion and
Flame, Volume 32, 1978, pp.
295-311.
38. Libby,
Paul A., and Blake, Thomas R.
"Theoretical Study of Burning
Carbon Particles" in Combustion and
Flame, Volume 36, 1979, pp.
136-169.
39. Libby,
Paul A. "Ignition, Combustion, and
Extinction of Carbon
Particles" in Combustion and Flame,
Volume 38, 1980, pp. 285-300.
40. Kassoy,
David R.; and Libby, Paul A.
"Activation Energy Asymptotics
Applied to Burning Carbon Particles"
in Combustion and Flame, Volume
48, 1982, pp. 287-301.
41. Matalon,
Moshe. "Complete Burning and
Extinction of a Carbon Particle
in An Oxidising Atmosphere" in
Combustion Science and Technology,
Volume 24, 1980, pp. 115-127.
42. Matalon,
Moshe. "Weak Burning and Gas-Phase
Ignition About a Carbon
Particle in an Oxidizing Atmosphere"
in Combustion Science and
Technology, Volume 25, 1981, pp. 43-48.
43. Baldwin,
Sam, ref II-79.
44. Prakash,
C.B. and F.E. Murray. "Studies on
Air Emissions from the
Combustion of Wood Waste" in
Combustion Science and Technology, Volume
6, 1972, pp. 81-88.
45. Bussmann,
P.J.T., P.
Visser, and K. Krishna
Prasad. "Open Fires:
Experiments and Theory" in Wood Heat
for Cooking.
This is also presented in Bussman, P., and
Prasad, K. Krishna, "Model
Predictions of Temperature and Velocity
Profiles in Turbulent Diffusion
Buoyant Flames." Proceedings of the
Seventh International Heat
Transfer Conference Vol. 12, pp. 401-406,
1982, Hemisphere Publishing
Corp., N.Y. and McGraw Hill International.
46. Emmons, Howard
W. and Armind Atreya. The Science of
Wood Combustion.
In Wood Heat For Cooking.
47.
Westbrook, Charles K. and Frederick L. Dryer.
"Chemical Kinetic
Modeling of Hydrocarbon Combustion"
in Proc. Energy Combustion
Science, Volume 10, Number 1, 1984, pp.
1-57.
48. Lee,
Calvin K. and J. Rodney Diehl.
"Combustion of Irradiated Dry and
Wet Oak" in Combustion and Flame,
Volume 42, 1981, pp. 123-138.
49. Sangen.
Ref. B-18.
50. Calcote,
H.F. "Mechanisms of Soot
Nucleation in Flames -- A Critical
Review" in Combustion and Flame,
Volume 42, 1981, pp. 215-242.
51. Glassman,
I. and P. Yaccarino.
"The Temperature Effect in Sooting
Diffusion Flames", Eighteenth
Symposium (International) on Combustion,
The Combustion Institute, 1981, pp.
1175-1183.
52. Kent,
J.H. and H.G. Wagner. "Soot
Measurements in Laminar Ethylene
Diffusion Flames", in Combustion and
Flame, Volume 47, pp. 53-65,
1982.
53. Smith et
al., refs II-107 to 112.
54.
Shih, T.M. Numerical Heat Transfer.
Washington, D.C.: Hemisphere
Publishing Corporation, 1984.
55.
Wesson, H.R., J.R. Welker, and C.M.
Sliepcevich. "The Piloted
Ignition of Wood by Thermal
Radiation", in Combustion and Flame,
Volume 16, 1971, pp. 303-310.
56.
Harris, reference II-15. See also Foley et.
al., reference II-156.
57.
H.S. Mukunda has found (personal
communication, October 27, 1986) that
good combustion is possible with
briquettes, sawdust, rice husk, or
other materials if done in a properly designed
combustion chamber.
Several innovative stove designs for use
with these materials are now
under development.
For further information, he should be
contacted
directly at ASTRA.
APPENDIX E
1.
Kakac, S.; Shaw, R.K.; and Bergles, A.E.
Eds. Low Reynolds Number
Flow Heat Exchangers, Washington, D.C.:
Hemisphere Publishing Company,
1983, 1016 pp.
2.
Kakac, S.; Bergles, A.E.; and Mayinger, F.
Eds. Heat Exchangers:
Thermal-Hydraulic Fundamentals and
Design, Washington, D.C.
Hemisphere Publishing Company, 1983, 1131
pp.
3.
Kays, William Morrow, and London, A.L.
Compact Heat Exchangers, Third
edition, New York: McGraw-Hill, 1984, 335
pp.
4.
Walker, G. Industrial Heat Exchangers,
Hemisphere Publishing Corporation,
Washington, D.C., 1982, 408 pp.
5.
Taboreh, J.; Hewitt, G.F.; and Afgan, N.,
Eds. Heat Exchangers:
Theory and Practice, Hemisphere
Publishing Corporation, Washington,
D.C., 1983, 979 pp.
6.
Heat Exchanger Design Handbook, 5 volumes,
Washington, D.C.: Hemisphere
Publishing Corp., 1983. Vol. 1: Heat
Exchanger Theory, Vol. 2:
Fluid Mechanics and Heat Transfer, Vol.
3: Thermal and Hydraulic
Design of Heat Exchangers, Vol. 4:
Mechanical Design of Heat Exchangers.
7.
Raznjevic, Kuzman. Handbook of
Thermodynamic Tables and Charts. New
York: McGraw-Hill, 1976.
APPENDIX F
1.
French, David. The Economics of Renewable
Energy Systems for Developing
Countries. Washington, D.C., June 1979.
2.
Baldwin, George B., "Why Present Value
Calculations Should Not Be Used
In Choosing Rural Water Supply
Technology", World Development, V.11,
N.12, pp.1075-1081, 1983.
3.
Thuesen, G.J., and Fabrycky, W.J.
Engineering Economy. Englewood
Cliffs, New Jersey: Prentice Hall, Inc., 6th Edition, 1984.
APPENDIX G
1.
Brownlee, K.A. Statistical Theory and
Methodology in Science and
Engineering. New York: John Wiley and
Sons, 1965.
2.
The sample standard deviation, s, is based
on a finite amount of test
data representing a small fraction of the
possible values were the
testing to be continued indefinitely. The
population standard deviation,
[sigma], is based on all the possible
values generated by testing
forever.
The two are related by the equation <see equation below>
bsex276a.gif (167x486)

so that the difference is significant
only for small test series with
few data points n.
3.
Note that this is not true but is a useful
fiction. Any particular
interval will or will not hold the true
average value. Only by
repeating a series of tests many times
can such a statement of
probability be made.
For example, if a series of 10 tests were
repeated 115 times (for a total of 1150
tests), all under identical
conditions with similar sample deviation,
then a fraction 100(1-2[alpha])%
of the ranges <see equation below>
bsex276b.gif (108x600)

will include the true average.
The subscript i refers to the different
test series above, not to individual
tests.
4.
Dixon, Wilfred J. and Frank J. Massey, Jr.,
Introduction to Statistical
Analysis, Third Edition, McGraw-Hill, New
York, 1969.
Note also that the more conventional
notation denotes this as the
[t.sub.[alpha]/2]-value rather than t-value.
The latter notation has been used
here for consistency with the notation
used for the confidence level,
etc. and for convenience.
5.
Strictly speaking, this statement is
wrong. In fact, one can only say
that if the average performances of
stoves A and B were the same, the
probability is more than 10 percent that
the t-value would exceed the
observed value of 1.30.
6.
More precisely, the u in equation (9) is u
= ([u.sub.1 - [beta]] + [u.sub.1 - [alpha]/2]) for a
two-sided test where [u.sub.1 - [beta]] is the probabilty of
correctly rejecting a
false hypothesis (the power of the test)
and [u.sub.1-[alpha]/2] is the probability
of correctly accepting the true
hypothesis (converse of the level of
significance).
The u are points of the cumulative normal distribution
function.
It should also be noted that for convenience the pooled
sample deviation has been assumed to be
equal to the standard deviation
of the underlying population distribution.
For further information
see reference 1 above.
(Note that the statements concerning the
number of tests needed in the draft
standards, reference V-1, are
wrong.)
7.
Remember in solving this that the square
root of a number can be both
positive and negative. Thus, to form the
ellipse both roots are used
in the equation to find the different
quarters of the ellipse.
APPENDIX H
1.
1984-85 Guide to Scientific
Instruments. Washington, D.C.: American
Association for the Advancement of
Science.
2.
Barford, N.C., Experimental Measurements:
Precision, Error, and
Truth, Addison-Wealey, London, 1967.
APPENDIX I
1.
Burmeister, ref B-2.
2.
Cebeci, ref B-3.
3.
Meinel, Aden B. and Marjorie P. Meinel;
Applied Solar Energy,
Addison-Wesley, Reading. Massachusetts,
1976.
4.
Duffie and Beckman. ref A-2.
5.
Handbook of Chemistry and Physics. 51st
Edition. Chemical Rubber
Publishing Company, 1970, 1971.
6.
Energy Factbook, Committee on Interstate
and Foreign Commerce, Print
96-IFC-60, November 1980, U.S.
Congress House of Representatives and
U.S. Library of Congress, Congressional
Research Service.
APPENDIX J
1.
U.S. Congressional Office of Technology
Assessment, Reference II-5,
background paper #2, May 1983.
2.
The World Environment Handbook, World
Environment Center, New York,
1985.
3.
Hall, Barnard, and Moss, reference II-20.
INDEX, BY AUTHOR
Abe, F. (II-14)
7, 16; (II-149)
253; (D-7) 175
Adisoemarto,
S. (II-92) 18
Adomeit, G.
(D-35) 183
Afgan, N.
(E-5) 187
Agarwal, B.
(V-25) 113
Aggarwal,
A.L. (II-107,109) 20
Aggarwal,
G.C. (II-117) 22
Alio, H.
(II-26) 8
American
Association for the
Advancement
of Science, (H-1) 221
American
Society for Testing and
Materials
(V-22) 83
Anderson, D.
(II-106) 19
Arnold,
J.E.M. (II-34) 8, 17, 19,
22, 23; (II-40) 8, 9, 17, 18
Arpaci, V.S.
(B-1) 149, 151, 153,
156
Arungu-Olende,
S. (II-8) 6, 12, 13
Ashworth, J.
(III-12) 40
Atreya, A.
(III-25) 55, 59; (D-12)
177; (D-46) 185
Aung, W.
(B-27) 156, 157
Axmed, M.C.
(V-17) 101
Babu, D.S.S.
(III-15) 41, 43
Back, L.H.
(B-28) 156
Bailie, R.C.
(D-25) 179
Bain, K.
(D-1) 175-179, 181
Balachandran,
B.N. (II-50) 8
Balakrishna,
M. (II-41) 8
Baldwin, G.B.
(F-2) 193
Baldwin, S.F.
(I-1) 1; (II-79) 17,
116, 117, 122-124; (II-80) 17,
27, 29, 66, 90-93; (II-120) 54;
(II-150) 14; (II-153) 26; (III-14)
41, 43, 54, 60, 90, 91,
151; (III-20) 54, 61, 90; (III-34)
60, 61, 90, 151
Bamford, C.H.
(D-17) 179, 181
Barford, N.C.
(H-2) 222-223
Barnard, G.W.
(II-20) 7, 8, 231,
251-254; (II-116) 20, 22, 24;
(II-151) 20; (II-155) 24; (III-41)
63
Beckman, W.A.
(A-3) 131
Bergles, A.E.
(E-1,2) 187
Bernow, S.
(II-24) 8, 11, 12, 14,
17
Beshty, B.S.
(D-37) 183
Bhagat, P.M.
(D-10,11) 177, 183
Bhaghavan,
M.R. (II-41) 8
Bhogale, S.
(III-15) 41, 43
Blackshear,
P.L. (D-8) 175, 177,
179, 181; (D-18 179, 181; (D-19)
179, 181, 182
Blake, T.R.
(D-38) 183
Bodoia, J.R.
(B-26) 156, 157
Bonney,
R.S.P. (II-74) 15
Booth, H.E.
(II-66) 14
Boureima, I.
(II-61) 253
Bowonder, B.
(II-147B) 253; (V-24)
101
Bradley, D.
(B-29) 156
Bradley, P.N.
(II-140) 24
Bradshaw, P.
(B-3) 149-151, 156,
157
Brambley,
M.R. (II-57) 8, 63; (V-22)
83
Breman, H. (II-91)
18
Broido, A.
(D-28) 181, 182
Brown, L.E.
(D-24) 179, 181
Brown, L.R.
(II-82) 17; (II-93) 18
Brownlee,
K.A. (G-1) 199, 203,
211, 220
Brunet, E.
(III-13) 40
Buckmaster,
J.D. (D-15) 179, 180,
185, 186
Burley, J.
(III-26) 55; (D-3) 175
Burmeister,
L.C. (B-2) 149, 151,
153, 156, 157, 162, 225
Burne, S.
(VI-4) 115-116
Bussmann,
P.J.T. (II-80) 17, 27,
29, 66, 90-93; (III-7) 28;
(III-27) 56, 58; (III-33) 58;
(B-11) 150, 151; (D-45) 185,
186
Cairnie, L.R.
(B-14) 151, 156
Calcote, H.F.
(D-50) 186
Cebeci, T.
(B-3) 149-151, 156,
157, 225; (B-31) 156, 157
Cecelski, E.
(II-9) 6, 8, 9; (II-55)
8
Center for
Science and Environment,
India (II-99) 19, 20, 22,
24
Cerutti, O.M.
(II-44) 8
Chaikan, R.F.
(D-26) 179, 181
Chandler, W.
(II-82) 17
Channeswarappa,
A. (II-50) 8
Chauvin, H.
(II-60) 9, 14
Chavangi, N.
(II-140) 24
Childers,
L.F. (III-3) 78
Chitty, R.
(B-13) 150
Christiaens,
M. (III-24) 55
CILSS Equipe
Ecologie-Forets (II-27)
8
Clement, J.
(II-28) 8
Conolly, R.
(B-12) 150, 151
Conte, S.D.
(B-20) 155
Council on
Environmental Quality
(II-7) 6, 8, 18, 251
Cox, G.
(B-13) 150
Crank, J.
(D-17) 179, 181
Dalbert, A.M.
(B-32) 156, 157
Dasappa, S.
(III-19) 41, 43, 53,
61
Dasgupta, B.
(II-147B) 253
Dave, R.M.
(II-107,109) 20
Davies, R.M.
(B-12) 150, 151
de Boor, C.
(B-20) 155
DeChambre, G.
(II-61) 253; (II-121)
23, 91, 93, 99
DeKoning,
H.W. (II-110)20
De Lepeleire,
G. (III-24) 55;
(III-37) 64; (B-21) 151, 156
Desrosiers,
R. (D-30) 181, 182
de Wit, C.T.
(II-76) 17
Department of
State (II-7) 6, 8,
18, 251
Diehl, J.R.
(D-48) 185
Digernes,
T.H. (II-130) 24
Dixon, W.J.
(G-4) 205
Dossi, H.
(II-101) 19
Down, S.
(II-58) 8, 9; (V-24) 101
Drake, R.M.
(III-9) 33; (A-1) 129,
149, 151, 153, 162, 163, 167,
169, 170
Dryer, F.
(D-47) 182, 183, 185
Dunkerley, J.
(II-9) 6, 8, 9; (II-33)
8; (II-36) 8, 22
Dunn, P.D.
(III-4) 27, 30, 115
Dutt, G.
(II-153) 26; (III-1) 28;
(III-10) 35; (V-10) 96; (V-20)
104; (VI-5) 123
Duffie, J.A.
(A-3) 131, 225
Earl, D.
(II-13) 8, 14, 16, 22,
252; (II-38) 8
Earnest, E.
(II-113) 20
Eckert,
E.R.G. (III-9) 33; (A-1)
129, 149, 151, 153, 162, 163,
167, 169, 170
Eckholm, E.P.
(II-2) 5, 18; (II-116)
20, 24
Emmons, H.W.
(III-25) 55, 59; (B-16)
150; (D-46) 185
Entwistle,
A.G. (B-29) 156
Estrada, F.S.
(II-44) 8
Fabrycky,
W.J. (F-3) 197
Felske, J.D.
(C-7) 171
Finn, D.
(II-88) 18
Fishwick, R.
(II-106) 19
Flavin, C.
(II-82) 17
Fletcher,
L.S. (B-27) 156, 157
FLORASA
(II-67) 14, 17, 24
Foley, G.
(II-77) 17; (II-116) 20,
24; (II-152) 23; (II-155) 24;
(II-156) 186; (III-41) 63
French, D.
(F-1) 193
Gaulard, R.
(C-4) 170
Geller, H.
(II-153) 26; (II-157/134)
25; (III-1) 28; (III-3)
27, 28, 30, 35; (III-10) 35;
(III-11) 40
Gentry, A.H.
(II-97) 18
Giorgini, A.
(B-6) 156
Glassman, I.
(D-14) 179, 180, 182,
185, 186; (D-51 186
Goldemberg,
J. (II-35) 8; (II-43)
8, 17; (II-157/133) 25
Gordon, L.
(II-9) 6, 8, 9
Graboski, M.
(D-1) 175-177, 179,
181; (D-31) 181, 182
Grainger, A.
(II-94) 18
Gray, D.R.
(B-6) 156
Guillaumet,
J.L. (II-101) 19
Gupta, R.K.
(II-157/137) 25
Gwynne, M.D.
(II-89) 18
Hadley, M.
(II-101) 19
Hall, D.O.
(II-10) 6, 8, 251; (II-20)
7, 231, 251-254; (II-54) 8
Harker, A.P.
(III-26) 55; (D-3)
175
Harris, A.C.
(II-15) 7, 176, 186
Harrison,
A.J. (B-14) 151, 156
Hartnett, J.P.
(B-9) 150, 153
Hashemi, H.T.
(D-24) 179, 181
Hassan, M.
(V-10) 96
Havens, J.A.
(D-24) 179, 181
Hewitt, G.F.
(E-5) 187
Hinrichson,
D. (II-42) 8
Holman, J.P.
(A-5) 139, 162
Horsley, M.E.
(B-19) 151
Howell, J.R.
(C-3) 167, 170
Hughart, D.
(II-11) 10
Hughes,
T.J.R. (b-22) 156
Hukai, R.Y.
(II-43) 8, 17
Hurley, J.R.
(II-157) 25; (III-23)
54
Hyman, E.L.
(II-56) 8,9; (II-131)
24; (II-132) 24; (V-16) 101;
V-21) 104; (VI-3) 115
Isaacson, E.
(B-20) 151
Islam, M.N.
(II-30) 8
Jackson, P.
(II-83) 18
Jagadish,
J.S. (III-15) 41, 43
Jaluria, Y.
(B-5) 149, 150, 151
Jongma, J.
(II-40) 8, 9, 18
Jordan, B.
(II-3) 5
Joseph, S.D.
(I-2) 1; (VI-5) 115
Joyce, N.
(III-4) 27, 30, 115
Kakac, S.
(E-1,2) 187
Kansa, E.J.
(D-26) 179, 181
Kanury, A.M.
(B-8) 153, 162; (D-8)
175,
177, 179, 181; (D-13) 179
180, 182, 183, 185, 186; D-18;
179; (D-19) 179, 181, 182; (D-20)
179, 181; (D-21) 179, 181
Karch, G.E.
(II-69) 14; (II-157/138)
25
Kartawinata,
K. (II-92) 18
Kashiwagi, T.
(C-13) 173
Kassoy, D.R.
(D-40) 183
Kays, W.M.
(E-3) 187
Keita, J.D.
(II-124) 23
Keita, M.N.
(II-25) 8
Keller, H.B.
(B-20) 151
Kent, J.H.
(D-52) 186
Kettleborough,
C.F. (B-32) 156
Khattals,
A.A. (B-31) 156, 157
King, N.K.
(C-9) 171
Kinyanjui, M.
(VI-1) 115; (VI-2)
115
KiZerbo, J.
(V-18) 101
Kjellstron,
B. (D-5) 175
Koenig, D.
(VI-16) 125
Komer, D.I.
(II-86) 18
Kristoferson,
L. (II-31) 8, 12
Krist-Spit,
C.E. (II-157) 25;
(III-35) 61, 119
Kumar, R.
(III-15) 41, 43
Kung, H.C.
(D-22,23) 179, 181
Kurosaki, Y.
(C-13) 173
Kuusela, K.
(II-17) 7
Lamont, R.
(B-31) 156, 157
Lamprey, H.F.
(II-105) 19
Larsen, P.S.
(B-1) 149, 151, 153,
156
Last, J.M.
(II-110) 20
Lee, C.K.
(D-48) 185
Lee, S.C.
(C-10) 171
Lee, S.L.
(B-16) 150
Leonard, B.P.
(B-30) 156
Leteemane, B.
(III-11) 40
Libby, P.A.
(D-39,40) 183
Lokras, S.S.
(III-15) 41, 43
London, A.L.
(B-10) 153, 164; (E-3)
187
Lopez-Parodi,
J. (II-97) 18
Lowes, T.M.
(C-6) 171
Ludford,
G.S.S. (D-15) 179, 180,
185, 186
Luhanga, M.L.
(II-47) 8, 9, 14,
24; (II-49) 8, 9
Lumar, S.B.S.
(III-19) 41, 43, 55,
61
Maa, P.S.
(D-25) 179, 181
Makhijani, A.
(II-52) 8
Malan, D.H.
(D-17) 179, 181
Massey, F.J.
(G-4) 205
Hatalon, M.
(D-41) 183
Mayinger, F.
(E-2) 187
Medynski, T.
(V-22) 83
Menon, P.
(II-108) 20
Meyers, N.
(II-85) 18
Hicuta, W.
(III-38) 64
Milne, T. (D-29)
181
Mintz, Y.
(II-100) 19
Mishima, H.
(C-13) 173
Mnzava, E.M.
(II-39) 8, 9, 22;
(II-59) 8, 9, 17
Modak, A.T.
(C-11,12) 173
Mohiuddin, G.
(D-35) 183
Moreira, J.R.
(II-157/133) 25
Morgan, R.P.
(II-57) 8, 63
Morgan, W.B.
(II-12) 6, 18, 23
Morse, R. (II-30)
8
Moss, P.A.
(II-20) 7, 8, 231, 251-254;
(II-54) 8
Moss, R.P.
(II-12) 6, 18
Moundlic, J.
(II-157/139) 25
Mukunda, H.S.
(III-18,19) 41, 43,
55, 61, 62; (D-57) 177.
Munslow, B.
(II-32) 8
Murray, F.E.
(D-44) 185
Mwandosya,
M.J. (II-47) 8, 9, 14,
24;
(II-49) 8, 9
Nagaraju,
S.M. (II-50) 8
National
Academy of Sciences (II-90)
18; (II-102) 19, 23, 24;
(II-124) 23, 127; (V-15) 101;
(D-6) 175
Nations, J.
(II-86) 18
Negrete,
M.A.M. (II-44) 8
Nelson, M.A.
(D-28) 181, 182
Newall, A.J.
(C-6) 171
Nkonoki, S.
(II-21) 8, 17, 253;
(V-24) 101
Noronha, R.
(II-125) 23, 24
Novikoff, G.
(II-103,104) 19
Nyyssonen, A.
(II-17) 7
O'Keefe, P.
(II-24) 8, 11, 12, 14,
17; (II-31) 8, 12, 19; (II-32)
8; (II-95) 18
Openshaw, K.
(II-18) 7
Osterle, J.F.
(B-26) 156, 157
OTA (II-5) 5,
18, 23, 24, 231
Ouedraogo, I.
(III-20) 54, 61, 90,
151; (III-34) 60, 61, 90, 151
Ozisik, M.N.
(A-4) 137, 140; (C-2)
167, 169, 170, 173
Palmieri, M.
(II-76) 16, 22
Pandey, U.
(II-22) 8, 20, 253
Pant, M.M.
(II-127) 24
Parkhurst, D.
(II-32) 8
Perlee, H.E.
(D-26) 129, 181
Perlin, J.
(II-3) 5
Peters, N.
(D-35) 183
Philips, P.
(II-32) 8
Pollack, J.
(II-1) 5, 18, 19
Poole, A.
(II-52) 8
Postel, S.
(II-82) 17
Poulsen, G.
(II-128) 24
Powers,
T.A.M. (III-11) 40
Prakash, C.B.
(D-44) 185
Prasad, K.K.
(II-63) 10; (II-115)
20, 24; (III-5) 27, 29, 49;
(III-7) 28; (III-21) 54; (III-27)
56, 58; (III-33) 58, 151,
171; (B-11) 150, 151; (D-45)
185, 186
Prasad,
S.S.R. (II-147B) 253
Pratt, D.J.
(II-89) 18
Pratt, G.H.
(III-32) 56
Purvis,
M.R.I. (B-19) 151
Pyle, D.L.
(D-3) 175, 181, 182
Ramakrishna,
J. (II-108) 20
Ramsay, W.
(II-9) 6, 8, 9; (II-36)
8, 22
Rao, N.P.
(II-147B) 253
Raskin, P.
(II-24) 8, 11, 12, 14,
17
Ravindranath,
N.H. (II-50) 8; (II-153)
26; (III-16,17) 41, 43;
V-24) 101
Raznjevich,
K. (E-7) 191
Reddy, A.K.N.
(II-45) 8, 9; (II-50)
8; (II-51) 8; (V-24) 101
Reddy, B.S.
(II-45) 8, 9
Reif, F.
(A-2) 129
Revelle, R.
(II-23) 8
Riswan, S.
(II-92) 18
Rivera S.
(II-157/135) 25
Roache, P.J.
(B-23) 156
Roberts, A.F.
(D-9) 176, 181, 182;
(D-27) 181
Roberts, O.C.
(D-34) 183
Rohsenow,
W.M. (B-9) 150, 153
Rose, A.B.
(II-73) 14
Salati, E.
(II-87) 18
Salem, B.B.
(II-129) 24
Samootsakorn,
P. (III-4) 27, 30,
115
Sandels, A.
(III-26) 55; (D-3) 175
Sangen, E.
(III-5) 27, 29, 49;
(III-27) 56, 58; (III-33) 58,
151, 171; (B-18) 151, 185
Sanogo, C.
(III-14) 41, 43, 54,
60, 90, 91
Savoie, M.
(V-17) 101
Selker, J.S.
(IV-3) 78
Sentle, J.
(III-11) 40
Sepp, C.
(V-11,12) 99, 100
Sernas, V.
(B-27) 156, 157
Servin, J.C.
(II-44) 8
Shah, R.K.
(B-10) 153, 164
Shaikh, A.M.
(II-157/138) 25
Shailaja, R.
(III-16,17) 41, 43
Shanahan,
Y.N. (I-2) 1
Shaw, R.K.
(E-1) 187
Shelton, J.
(III-31) 56
Sherman, M.
(VI-7) 115
Shih, T.M.
(B-24) 156; (B-25) 156;
(D-54) 186
Shirwa, Z.C.
(V-17) 101
Shrestha,
K.L. (II-46) 8
Shrinivasa,
U. (III-18,19) 41, 43,
55, 61, 62
Shukla, J.C.
(II-157) 25; (III-23)
54
Shukla, J.
(II-100) 19
Sibulkin, M.
(C-8) 171
Sidibe, Y.
(III-14) 41, 43, 54,
60, 90, 91
Siegel, R.
(C-3) 167, 170
Simonis, P.
(II-80) 17, 27, 29,
66, 90-93
Singh, J.S.
(II-22) 8, 20, 253;
(V-24) 101
Singh, N.T.
(II-117) 22
Skouri, M.
(II-103) 19
Sliepcevich,
C.M. (D-55) 186
Smale, M.
(V-17) 101
Smil, V.
(II-81) 18
Smith, J.W.
(D-34) 183
Smith, K.R.
(II-107 to 112) 20,
21, 28, 186; (III-29) 56
Smith, N.J.H.
(II-96) 18
Soesastro,
M.H. (II-30) 8
Somashekar,
H.I. (II-50) 8
Sorenson, B.
(II-21) 8, 17, 253;
(V-24) 101
Spears, J.
(II-98) 19, 20
Srisom, B.
(VI-7) 115
Steinlin,
H.J. (II-84) 18
Stevens, W.C.
(III-32) 56
Steward, W.
(VI-7) 115
Stewart, W.
(I-2) 1
Stevens, N.F.
(II-74) 15
Storke, L.
(II-82) 17
Strasfogel,
S. (II-119) 23; (II-121)
23, 91, 93, 99; (III-14)
41, 43, 54, 60, 90, 91
Sulilatu,
W.F. (II-157) 25
Taboreh, J.
(E-5) 187
Tariq, A.S.
(B-19) 151
Thai
Government, Forest Products
Division
(II-72) 14, 22; (IV-2)
78, 115
Thuesen, G.J.
(F-3) 197
Tien, C.L.
(C-7,10) 171
Timberlake,
L. (II-116) 20, 24
Tiwari, A.K.
(II-22) 8, 20, 253;
(V-24) 101
Tiwari, K.M.
(II-53) 8
Toon, O.B.
(II01) 5, 18, 19
Toong, T.Y.
(D-16) 179, 180, 185,
186
Ubhayakar,
S.K. (D-36) 183
UN (II-6) 6,
12, 23, 251; (II-65)
18, 254
UNDP (II-154)
23
UNFAO (II-4)
5, 8; (II-19) 7; (V-14)
101
Uhart, E.
(II-68) 14
van Buren, A.
(II-77) 17
van Gelder,
A. (II-140) 24
Van Nao, T.
(II-129) 24
Vayda (II-92)
18
Vidyarthi, V.
(II-118) 22
Visser, P.
(III-7) 28; (III-27)
56; (III-33) 58, 151, 171; (B-11)
150, 151; (D-45) 185, 186
VITA (V-1)
82; (V-2) 82
Vose, P.B.
(II-87) 18
Wagner, H.G.
(D-52) 186
Walker, G.
(E-4) 187
Wardle, P.
(II-76) 17, 22
Wartluft, J.
(II-71) 14, 22
Weber, F.
(II-78) 17
Wegner, K.F.
(II-16) 7
Welker, J.R.
(D-24) 179, 181; (D-55)
186
Wesson, H.R.
(D-55) 186
Westbrook,
C.K. (D-47) 182, 183,
185
White, S.
(II-71) 14
Williams, F.
(D-32) 181; (D-33)
181, 182
Williams,
R.H. (II-64) 10; (II-136)
26; (II-157/136) 25
Wolfe, E.
(II-82) 17
Wood, T.S. 5,
(II-70) 14; (II-150)
14; (III-36) 62; (V-19) 104
World Bank
(II-154) 23; (II-126)
23; (II-147C) 254
World
Environment Center (J-2) 231
Yaccarino, P.
(D-51) 186
Yameogo, G.
(II-80) 17, 27, 29,
66, 90-93; (III-20) 54, 61, 90,
151; (III-34) 60, 61, 90, 151
Young, P.J.
(III-3) 78
Yussuf, H.
(II-105) 19
Zaror, C.A.
(D-3) 175, 181, 182
Zhu, H.
(II-57) 8, 63
INDEX, BY SUBJECT
Absorptivity,
see emissivity
Acceptability
surveys, 103
Airholes, 61,
73-74, 80
Air to air
heat exchanger 125-127,
187-191
Altitude,
effects on testing, 85
Animal Dung,
7, 19, 20, 22, 252
Arrhenius
rate law, 180-181
Artisanal
production, 49, 50, 65
ASTRA, 43, 65
Average, 92,
199-200
Baffles, 61,
86, 185
Balance, 83,
117-118, 221
Bangladesh, 6
Biases, in
field surveys, 102
Black body,
50-52, 167-172
Biomass, 2,
6-13, 17-18, 23-25
consumption, 6, 8-13, 17-18
resources, 7,8
Bomb
calorimeter, 175, 222
Boussiness
approximation, 156
Boundary
Layer, 42, 43, 160-162
Briquetted
fuels, 60, 177
Calorific
values, 55-57, 175, 178,
179
Carbon
dioxide, 59, 182-186
Carbon
monoxide, 59, 182-186
in charcoal stoves, 17, 122
in gasifiers, 63
in nozzle stoves, 43
Cellulose,
56, 58, 176, 182
Ceramic
stoves, 66, 78-80, 90, 100
Channel
dimensions, 42, 123, 125
efficiency, 45-48, 85
Channel
stoves, 42-50, 65, 80, 90,
93, 99, 151-166
Characteristic
length, 157
Charcoal,
13-18, 182-185
calorific value, 7, 176, 179
combustion, 182-185
conversion efficiency, 14-15
demand, 17-18
density, 7
industrial uses, 17-18, 125-127
kilns, 13-14
transport, 14-17
volatiles, 7, 176
Charcoal
stoves, 115-125
energy Balance, 30
foundries, see foundries
performance, 122-125, 219-220
Chimneys, 68,
71, 86
Coefficient
of variation, 202-203
Combustion,
55-61, 175-186
efficiency, 31
losses, 28-30
Combustion
chamber geometry, 61,
185
Common
residual variance, 214
Concrete, 66
Conduction,
2, 31-41, 129-147
of wood in a fire, 59
Conductivity,
33-35 132, 154, 163,
179, 180
Confidence
limits, 204-205
Confidence
region, 208-210, 212-213
Contaminants,
effect on pyrolysis,
181
Control
efficiency 31, 62-64, 260-262
Control
groups in field surveys,
105-106
Controlled
cooking tests, 91-96
Convection,
3, 32, 41-50, 149-166
Losses, 28-30
Cooking
energy, 8-11 27-28
Cooking
process efficiency, 31
Cookstoves, 2
Correlation
coefficient, 208, 218
Crop
Residues, 6-7, 10, 19
Dampers, 62
Data
analysis, 86
Dead air
space, 38-40, 139
Deforestation,
5, 6, 18, 19
Degrees of
freedom, 201, 206
Density, 33,
129, 132, 163
Developed
flow, 157
Dimensional
errors, 3, 66-68, 70,
156
Domestic
energy use, 8-10
Doors, 41,
60-62, 74, 86
Double walls,
38-40, 66-67
Dry basis,
56-57
Duct flow
150-157
Dung, see
animal dung
East-West
Center, 20, 101
E/DI, 115
Economics,
20, 22-23, 92, 193-198
Efficiency
factors, 31
Electroplating,
66
Emissions,
19-21, 93, 151, 185-186
of nozzle stove, 43
Emissivity,
38-40, 51, 167, 169-173
Energy
balances, 28-30
Energy
demand, 8-13, 17-18
Energy
storage, 35, 135
Environment,
18-20
Errors in
dimensions, 3, 66-68,
70, 156
Errors in
testing equipment,
analysis of,
222-223
Erosion,
18-19
Excess air,
60-61, 155
F-distribution,
209, 211
Fan power,
125, 127, 190
Fanning
friction factor, 159, 153
Field test,
101-112
Financial
analysis, 193-198
Fired clay --
see ceramic
Firepower,
84, 86, 89, 118, 155,
186
Flames, 150,
151, 171, 185, 186
Flywheel
press, 78
Foraging,
20-22, 249
Forced convection
160-161
Forest, 5, 6,
, 18-19, 251
Forges,
125-127
Fossil fuels,
22-23, 25, 178
Foundries,
see forges
Friction
factor, see fanning
Fuelwood, see
woodfuel
Furnaces, see
forges
Future worth,
195-198
Gap, 42
Gas analysis,
222
Gasifiers, 62
Grashof number
157, 159-162
Grate to pot
height, 51-54, 85
Grates, 60,
75, 77, 80
Grog, 66
Gross
calorific value, 55, 257
Haybox
cooker, 36, 64
Heat
exchangers, 125-127, 187-191
Heat
recuperation, 36, 38, 39
see also heat exchangers
Heat storage,
32, 135
Heat transfer
correlations, 159-162,
164
Heating rate,
48-49, 136-140
Hemicellulose
56, 58, 178
Higher
heating value, 55, 257
High power
phase, 83, 89
Humidity,
relative, 56
Hydraulic
diameter, see characteristic
length, 159
Hydraulic
presses, 78
Ideal gas
law, 157
Industry
energy use, 9, 11, 12, 17
Insect attack
of wood, 17
Institutions,
231-239
Insulants,
34, 86, 132
Interest
rate, 193-198
Internal
molds, 78
Internal rate
of return, 197-198
International
testing standards,
82
ITDG, 115
KENGO, 115
Kenya, 11, 12
Kilns for
drying wood, 222
Kilns for
producing charcoal, 13-15
KREDP, 115
Laboratory
tests, 81-91
parameters to be tested, 85-86,
119, 122
precautions, 85
procedure, 82-84, 116-119
Laminar, 115,
158, 159-162
Level of
confidence, 201, 203, 206
Lightweight
stoves, 35-41, 65, 90
Lignin, 56,
58, 176
Linear
regressions, 207-220
Lower heating
value, 55, 257
Low power
phase, 83, 89
Malgache, 90,
123, 124
Marketing
tests, 113-114
Massive
stoves, 29-30, 34-37, 65-66,
90, 93, 100
Moisture
content, 56-57, 259
Moisture
meter, 222
Multipot
stoves, 65-66, 90, 93,
100
control, 62
energy balance, 29-30
Natural
convection, 161, 162
Net calorific
value, 55, 257
Newtonian
fluid, 158
Normal
distribution, 199, 201
Nozzle stoves
42-44, 55, 65, 151
Numerical
techniques, 137-140
Nusselt
number, 151, 158, 159-162
Observables,
111
Outlier, 204
Peclet
number, 158
PHU, percent
heat utilized, 51,
82, 84, 89, 92, 119, 122-124
Plantations,
23-24
Plenum
chamber, 125-126
Plume,
150-151
Pooled sample
deviation, 205
Pooled
residual variance, 212
Pooled
t-value, 214
Population
by cooking fuel, 10, 12
Pot, 31,
34-35, 64, 68
efficiency, 31, 34-35, 64
supports, 41, 74, 77, 80, 86
Potters
wheels, 78
Power
consumption, 8
Prandtl
number 153, 158, 163
Preheating
air, 61, 125-127
Present
value, 195-198
Pressure
cookers, 64
Pressure
drop, 153, 164, 190
Production
tests, 97-100
Promotion,
113
Proximate
analysis, 175-176
Public
demonstrations, 113
Pyrolysis,
179-182, 185-186
Radiation,
28-30, 38-41, 50-55,
77, 138-139, 167-173
in charcoal stoves, 116-117
role in wood combustion, 58
Rayleigh
number, 158
Recuperation,
see heat recuperation
Regression,
see linear regression
Relative
humidity, 56
Retorts,
13-15
Reynolds
number, 153, 158-162
Rollers,
sheet metal, 76
Sample
deviation, 200-202, 204
Sample size
required, 207
Scale
factors, 96, 157, 164
Scorecards,
93, 95-96
Secondary
air, 61, 122
Single pot
stoves, 62-63, 65-67,
90
Site
construction, 49-50
Smoke, see
emissions
Soils, 19
Soot, see
emissions
Spacers, to
center pot, 75
Specific
consumption, 82, 84, 89,
92, 94, 119, 123-124, 264
Specific
daily consumption, 110
Specific
heat, 33, 35, 129, 132,
154, 163
Stagnation
point, 150-151, 160-162
Standard
deviation, 92, 200-201
Standard
meal, 91
Stanton
number 158
Steady state
heat loss, 129-136
Steel, 17,
25-26, 66
Stefan-Boltzmann
law, 167
Steres, 7
Stoichiometric
air, 59, 155, 178
Stove
efficiency, 31
Stoves
accessories, 68, 70
adjustable to pot, 50
construction, 65-70
production, 76-80
shapes, 67-69
types, 42
Sumatra,
west, 9
Surface
boundary layer, see
boundary layer
Surface heat
loss, see wind, 139
Surveys, see
field tests
Swirl, 61,
185
t-table, 203
t-test, 92,
205-207
Tape measure,
221
Temperature
gradient, 67, 136
Template
design, 72-75
Tests, 3,
81-114, 116-122
controlled cooking, 81, 91-96
field, 81, 101-112
laboratory, 81-91, 116-122
marketing, 82, 113-114
production, 76-80, 81, 97-100
results, 90, 93, 98-100, 123,
124
Thermal
conductivity, 31-41, 129-147
Thermal
diffusivity, 129, 158, 163
Thermal
efficiency, 31
Thermal
inertia, 35
Thermal mass,
35
Thermal
storage, 32, 35
Thermocouples,
221
Thermometers,
83, 117-118, 221
Traditional
stoves, 8-13, 17-18,
20, 22, 25, 29, 66, 90, 93,
123, 124
energy balance, 29
Transient
heat conduction in wood,
180-181
Transient
heat loss, 136-140
Transportation
energy, 14-18
Turbulent
flow, 158, 160-162
Ultimate
analysis, 175, 177, 179
Umeme, 123
Ungra, 8
Units, 7, 9,
225-230
Variance, see
standard deviation
Variance of
residuals, 208, 212
Vendors, 113
View factor,
51-54, 170-173
Viscosity,
154, 158, 163
Volatiles
charcoal, 7, 182
wood, 57-59, 179-182, 185-186
Volume
coefficient of expansion,
158
Wall jet,
150-151
Wall losses,
28-30, 35-41, 129-147
Wall
temperatures, 40
Walls, 35-41,
66-80
double, 37-40, 66-67
fired clay, 37, 39, 40, 41, 66-69,
78-80
insulated, 37, 39-41
lightweight, 37-41, 65-66
massive, 36, 65-66
single, 37-40, 66-77
Warranty, 113
Welding, 77
Wet basis,
56-57
Wind, 34, 85,
131
Wood economy
surveys, 103-105
Woodfuel,
6-12
consumption, 8-12
deficits, by population, 12
foraging, 20
resources, 7
========================================
========================================

