SPREADSHEETS TUTORIAL
EXAMPLE : SOLVING POLYNOMINAL EQUATIONS
Example: Solve 2x3+ 6x2 - 9x -12
= 0
Solution:
To solve 2x3+ 6x2 - 9x -12 = 0,
you have first to draw a graph of y = 2x3+
6x2 - 9x -12
PART 1 : Ploting the Graph of y = 2x3+
6x2 - 9x -12
Step 1: Plot a Graph of y = 2x3 + 6x2
- 9x -12
(a) Type X in
B7 and Y in C7
Block the range B8 through B24 and name this range x.
Insert ---> Name ----> Define
(b) In C8, type the formula = 2*x^3 + 6*x^2 -9*x
-12
(c) Type -5 in B8
Autofill the cells B8 to B24 in steps
of 0.5
Block cells B8 to B24
Edit ---> Fill ---> Series
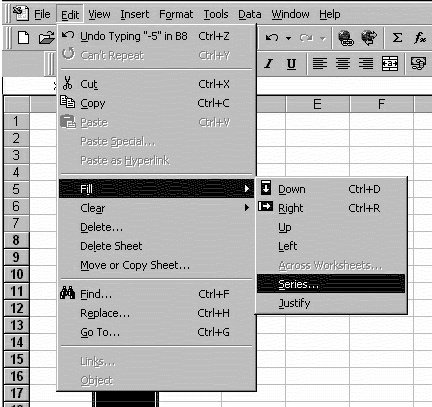
Choose
Series in : Columns
Type : Linear
Step value : 0.5
Stop value : 3

Click OK
Copy the formula in C8 and paste it in the range C9 to C24.
(d) Choose the the XY (Scatter) graph type shown below.
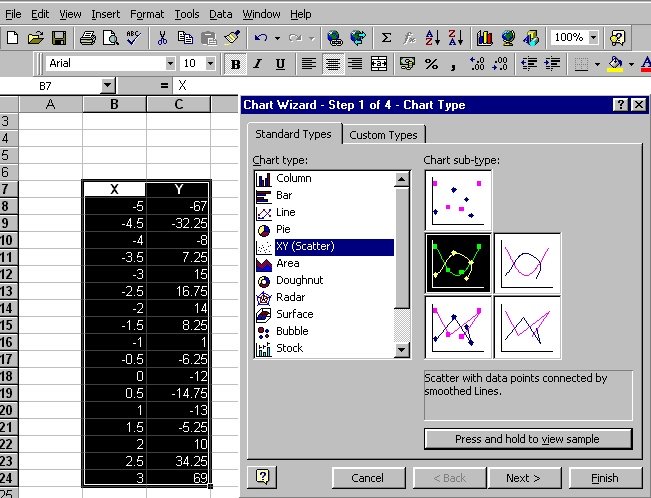
Complete the process of drawing the Chart (graph)
he graph is as shown below

Link to the
Graph.
Part 2 : Solving 2x3 + 6x2 - 9x
-12 = 0
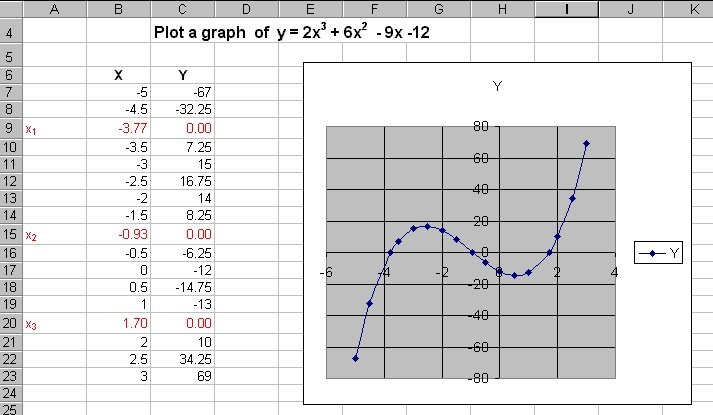
We need to find the values of x when y = 0 or the intercepts
on the X-axis. The graph of y = 2x2 + 6x2
- 9x -12 shows that there are three values of x: x1,
x2and x3. Two of these values
are negative and one positive.
To find the values x1, x2, x3
use the Goal Seek tool under Tools on the menu
bar.
Goal Seek adjusts the value in a specified cell
until a formula that is dependent on that cell reaches a target
value
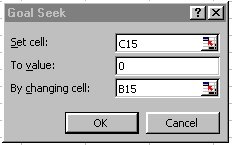
In this case Goal Seek will adjust the value in cell B15
until until the formula in C15 reaches a target value of 0.
Note:
The values of Y change from:
-8 (negative) in cell C9 to +7.25
(positive) in cell C10
1 (positive) in cell C15 to
-6.25 (negative) in cell C16
-5.25 (negative) in cell C20 to +10 (positive)
in cell C21
To obtain the values of x: x1, x2 and
x3, use the Goal seek tool and set the values in
cells C9 or C10, C15 or C16 and C20 or C21 to a target value
of 0.

Use the following values
|
Set cell
|
C9 |
C15 |
C20 |
|
To value
|
0 |
0 |
0
|
|
By changing cell
|
B9 |
B15 |
B20 |
Link to
the Graph
The polynomial 2x3 + 6x2 -
9x -12 = 0 has three solutions; x1 = -3.77, x2
= -0.93, x3 = 1.70
|







